0 1 solution of linear programming problem with only equality constraints

Question

I have a linear programming problem $LP$ where all the variables $x_{i}$ take value in $\left[0, 1\right]$ (that is $0\leq x_{i} \leq 1$). All the constraints are as follow: $a_{1}+a_{2}+a_{3}=1$ that is each constraint is the sum of three distinct elements, for each elememt $a_{j}$ with $j\in \left\{1; 2; 3\right\}$ we have $a_{j}=x_{i}$ or $a_{j}=1-x_{i}$ and each sum is equal to $1$. It is not possible that the same variable $x_{i}$ appears two times in the same sum.

If for each variable $x_{i}$ we have that $LP$ is feasible whether we set $x_{i}=0$ or $x_{i}=1$, can we say that exists an integer solution of $LP$, that is a solution where each variable takes value in $\left\{0; 1\right\}$?

I give an example to make clearer my question.
Given:
$x_{1}+x_{2}+x_{3}=1$
$x_{4}+(1-x_{5})+x_{6}=1$
$(1-x_{7})+x_{8}+x_{9}=1$
$(1-x_{1})+(1-x_{5})+(1-x_{7})=1$
$0\leq x_{i} \leq 1$ $\forall i$

Foreach variable $x_{i}$ of the problem, one by one, we have that the problem is feasible whether we set $x_{i}=0$ or $x_{i}=1$.
The problem has at least an integer solution: $x_{1}=1$, $x_{2}=0$, $x_{3}=0$, $x_{4}=1$, $x_{5}=1$, $x_{6}=0$, $x_{7}=0$, $x_{8}=0$, $x_{9}=0$.

The question is: in general, for a problem where the constraints are the sums of three variables or their complement to $1$, the sums are equal to $1$ and $0\leq x_{i} \leq 1$ $\forall i$ (like in the given example), is it true that if the given problem is feasible whether we set, one by one, $x_{i}=0$ or $x_{i}=1$ foreach variable $x_{i}$ of the problem, then there is at least an integer solution of the given problem?

Answer 1

If I am not mistaken the answer is NO unless $P=NP$. We can reduce Exactly-1 3-satisfiability to your problem. For a proof of 1-IN-3SAT is NP-complete see NP-Completeness of 3SAT, 1-IN-3SAT and MAX 2SAT.

Given an instance $I$ of the Exactly-1 3-satisfiability problem. For each variable $x_i$ check whether there is a solution setting it to $1$ and $0$. This can be done solving $2n$ LPs. Then there are three cases:

1. All variables have a solution with $1$ and $0$. Then we are in the case you described and we know there is an integer solution.
2. There is a variable with no solution for both cases ($1$ and $0$). Then we know there is no solution for the entire problem.
3. None of the above is the case and there are variables satisfying exactly one of the two cases. Then we can fix these variables to the cases that do work and reduce the problem size. During this reduction we have to do some extra work described in the following.

In step three we might end up getting constraints of the form: $$ \begin{align} a_1 &= \begin{cases} 0 \\ 1\end{cases}\\ a_1+a_2 &= 0 \\ a_1+a_2 &= 1. \end{align} $$ In the first case we can simply fix the variable encoded in $a_1$ and continue cleaning up. The same holds for the second case, where we get $a_1=a_2=0$.

For the third case we can replace the variable in $a_2$ by the variable in $a_1$ such that the constraint is always fulfilled ($a_2 = 1-a_1$). By this it might happen that we end up getting constraint containing one $x_i$ multiple times. This is also not a problem, as this either fixes $x_i$ to be always $1$ (in cases we have $2x_i$), always $0$ (in cases we have $2(1-x_i)$) or adding a constant to the constraint (in cases $1-x_i+x_i$). In this case $x_i$ can be removed from the constraint and either the constraint disappears entirely or we end up with something like $a_1 = \begin{cases} 0 \\ 1\end{cases}$, which we already solved.

If during this reduction we find the problem to be infeasible we know it is infeasible. Otherwise we can start over on a smaller problem.

After at most $n$ iterations all variables were replaced or we ended up with case 1. or 2., thus the algorithm terminates in polynomial time.

I hope this helps and in case I made any mistakes please point them out. ;)

Answer 2

The question can be understand as determining the truth value of $$(\forall \text{assignments}: \text{relaxation feasible} )\implies \text{problem has integer solution}.$$

However since setting up many LP problems is more expensive then solving a small MILP (or even cheaper 1-in-3 SAT). I instead try to show the opposite: $$(\forall \text{assignments}: \text{relaxation feasible} )\land \neg(\text{problem has integer solution)}.$$

A not quiet naive approach that works for 4 variables

I tried to find an counter example but wasn't able to put in the engineering effort to remove all the symmetries so my approach only scales to 4 varibles.

I attempted to do that for all 4 variable formulas with the following (hacky and ugly) Julia code.

using JuMP
using Gurobi
coll = []
function build_constraint(model, vars, constraint)
  rhs = 1
  signs = similar(constraint)
  for i in eachindex(constraint)
     if sign(constraint[i]) == -1
       signs[i] = -1
       rhs -= 1
     else
       signs[i] = 1
    end
  end
  @constraint(model, sum(signs[i]*vars[abs(constraint[i])] for i in eachindex(constraint) ) == rhs)
end
function flip_signs(head,tail,func)
  if isempty(head)
    func(tail)
  else
    hd = head[1]
    for i in Iterators.product(-1:2:1,-1:2:1,-1:2:1)
       c =  copy(tail)
       flip_signs(head[2:end], push!(c, i .* hd), func)
    end
  end
end
function build_model(constraints)
  m = Model(Gurobi.Optimizer)
  @variable(m,x[1:4],Bin)
  for c in constraints
    build_constraint(m, x, c)
  end
  set_silent(m)
  optimize!(m)
  if termination_status(m) != MOI.OPTIMAL
    println("Interesting: ",constraints)
    push!(coll, constraints)
  end
end
flip_signs([[1,2,3]], [], build_model)
flip_signs([[1,2,3],[1,2,4]], [], build_model)
flip_signs([[1,2,3],[1,2,4],[2,3,4]], [], build_model)
flip_signs([[1,2,3],[1,2,4],[2,3,4],[1,3,4]], [], build_model)
counter = []
function build_linear_models(collection)
  for constr in collection
    m = Model()
    @variable(m,0<=x[1:4]<=1)
    for c in constr
      build_constraint(m, x, c)
    end
    isalwaysfeasible = true
    for i in 1:4
      for v in 0:1
        m2 = copy(m)
        set_silent(m2)
        set_optimizer(m2, Gurobi.Optimizer)
        @constraint(m2, variable_by_name(m2,"x[$(1)]") == v)
        optimize!(m2)
        isalwaysfeasible = isalwaysfeasible && (termination_status(m) == MOI.OPTIMAL)
      end
    end
    if isalwaysfeasible
      push!(counter,constr)
      println("Counterexample: ", constr)
    end
  end
end
build_linear_models(coll)
if isempty(counter)
  println("nothing found")
end

I first collect all instances Gurobi couldn't solve successfully and then check whether any of these passed the relaxation test. I found no counter examples with 4 variables. I did that by checking the 4 equivalence classes of hypergraphs made solely out of 3-hyperedges that cover a 4 element fully connected graph. There are 4 of them and then try every single sign flipped version of 5. This however scales really badly for 5 variables. As the formula containing all distinct 3 literal clauses of 5 variable are of count $2^{3\binom{5}{3}} = 2^{30}$ of which a larger fraction are redundant. (Think 1 in sum over some factorials is not a duplicate, did not make a more precise analysis but 1 in 10! is an overestimate of the degree of duplication.

How would i go about it if it was my job

This problem quickly becomes intractable as naive approaches would already fail at 4 variables and my slightly advanced approach of generating the which variables are inside a clause independent of the conversion into literals fails for 5 variables. (By failing i mean takes to long and next step will be much, much worse (I think i could make a good case for super-exponentially worse))

The biggest priority is write a system that generates one example for every equivalence class of non-redundant 3 sat formulas. Two formulas are in the same equivalence class if there exist an one-to-one and onto mapping from the variables and their negatives into the variables and their negatives such as the formula matches all solutions can be translated into solutions of the other formula using that mapping.

The approach is to construct from the empty formula (or deconstruct from the full formula) a 3-hypger graph where each 3-edge doesn't violate the variable occurs twice rule.

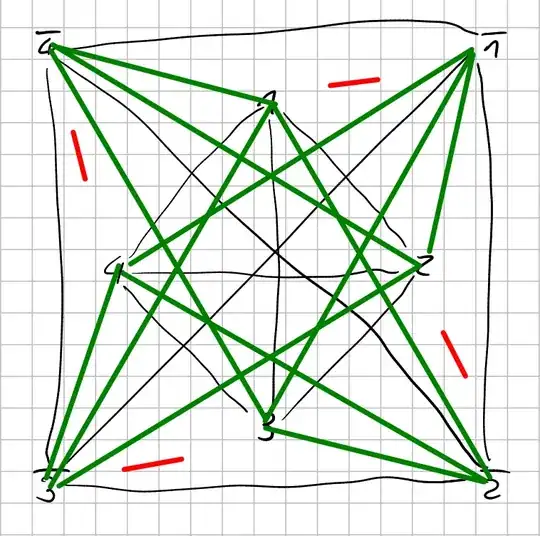
You see nodes for the literals $1$ thtough $4$ and their negation. A 3 hyperedge is only valid if each node it connects is directly to connected to every other node in the 3-hyperedge in the graph above. Notice the absence of connection between literal and their negation to enforce your constraint.

To prevent the creation of redundant formulas it essential (and probably sufficient) to track symmetric literals/nodes 1 in the 3-hypergraph and when expanding the search tree on that node don't expand it in a way which would add two child nodes which have a new 3-edge that is identical given the node symmetries in the parent. Another thing to be aware is that the search tree is actually a Directed Acyclic graph, as there are multiple ways of adding hyperedges to end up with same hypergraph. So a checking for 3-hypergraph equivalence needs to be performed between every hypergraph at each depth. There are some heuristics that can allow you to bail out early when comparing and i haven't explored but find it likely that the DAG structure might also poses constraint which nodes can bring forth similar equivalent children.

Also note that adding an edge can include up to 2 literals which weren't in the parent and their negation wasn't either, however not 3 literals which weren't in the parent as you are only interested in growing connected 3-hypergraphs, as non connected ones are independent sub problems with fewer literals you would have searched when you did a run with that many variables. It is possible to add 3 new literals though if one of the has a negation in the parent.

For $n$ variables the will be graphs with length from 0 to $\binom{n}{3}$ this search DAG however there is an symmetry in the search DAG i hinted at the beginning, namely a $m$ 3-edge hypergraph has $\binom{n}{3} - m$ 3-edge hypergraph as negation.

An algorithm that satisfies these notes should be able generate only one and one member from all equivalence classes of that many variables. However a formal treatment might discover i missed something.

The next most important thing is to speed up the batch solving of the very, very similar LP problems that arise. It is possible GPU acceleration is beneficial here.

The last step at scale is to modify an existing fast starting SAT solver into an 1-in-3 SAT solver, as that the 1-in-3 SAT problems can be solved a lot faster that way than an SAT encoding. It would be furthermore advisable to remove presolving. If this becomes a larger bottleneck it might be worth to look into SAT solvers for random formulas as they have special techniques that could work well when ported over to 1-in-3 SAT.

A last thing into keep in mind is that the LP check and the 1-in-3 SAT call can be easily distributed even on something with as weak coupling as BOINC. If you have more workers than you can satisfy with one computer producing the equivalence class representatives you can have a second computer works on generating problems a different number of variables. The reason why i want to discourage distributing this part is that you need and all to all nodes in the search DAG communication and 3-hypergraph equivalence checks across these links (this would be possible with MPI in an HPC environment but i imagine the pain not being worth it until you start to run out of memory on as a big a server as you can afford having many of). The equivalence class generation happens more efficiently on a single node and there are no two points you can start searching independently (expect empty and full but you can generate the other by inverting the other anyway) without risking duplicate clauses or having to check for equivalence later. One equivalence when expanded leads all children also being explored redundantly.

Solving this problem in scalable way will require a non-trivial new algorithm, modifying exiting libraries, new research into batch LP solving. If it doesn't find an counter example it wouldn't completely wasted as it will probably yield new insights into SAT solvers as the study of the equivalence classes might reveal new patterns.

This post should give you a good battle plan how two researchers could setup this in a few months. I can make no estimate on how much compute will be needed, as we don't know how the number of equivalence classes of 3-SAT instances (without repeated variables) scales with the number of variables.

Another approach to falsification: Encode hard SAT formulas into 1-in-3 SAT and check your prediction vs the know result agreed upon multiple solvers.

1 Generalize this notion of graph symmetry to 3-hypergraphs