5

Let $l,u\in\mathbb{R}^n$, and consider the QP:

$$\min_{l\le x\le u} {(\Delta x)^\top (\Delta x)}$$

where $\Delta x=[x_2-x_1,\,x_3-x_2,\,\dots,\,x_n-x_{n-1}]^\top$.

I.e. we want to minimize the squared change in the elements of $x$ subject to $x$ being above the lower bound $l$ and below the upper bound $u$.

My hunch is that this is simple enough that it ought to have an exact "pooled adjacent violators algorithm (PAVA)" style solution. Is this correct? Has this problem been studied in the prior literature?

Aside: Of course as stated here the problem may have multiple solutions. I do not care which is returned.

Further aside: Here's MATLAB type code for an inefficient solution procedure. I expect there's a much more efficient algorithm!

while true

xo = x;

x( 1 ) = max( l( 1 ), min( u( 1 ), x( 2 ) ) );
for i = 2 : ( n - 1 )
    x( i ) = max( l( i ), min( u( i ), 0.5 * ( x( i - 1 ) + x( i + 1 ) ) ) );
end
x( n ) = max( l( n ), min( u( n ), x( n - 1 ) ) );

if all( abs( x - xo ) < 1e-12 )
    break
end




end
cfp
  • 259
  • 1
  • 8

1 Answers1

5

I found the problem interesting, so I designed an algorithm to solve it (not PAVA-style). You can find a Python implementation here.

A geometric formulation

The optimality conditions are, for $1 \lt i \lt n$:

  • $x_i - x_{i-1} = x_{i+1} - x_i~$ if $l_i \lt x_i \lt u_i$
  • $x_i - x_{i-1} \leq x_{i+1} - x_i~$ if $x_i = u_i$
  • $x_i - x_{i-1} \geq x_{i+1} - x_i~$ if $x_i = l_i$

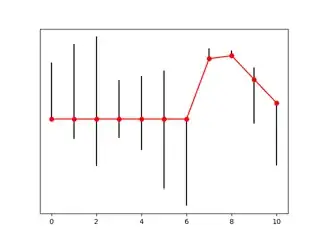
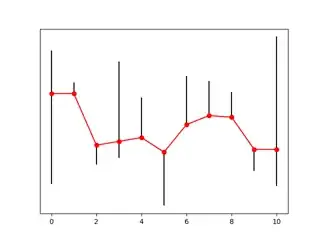
Using those, we can replace it by a geometric problem with the same optimal solutions. For each $i$, there is a vertical line with $x=i$ and $l_i \leq y \leq u_i$. The goal is to find the shortest path going through all these segments from left to right. Any bend in this path will correspond to $x_i = l_i$ or $x_i = u_i$.

An example:

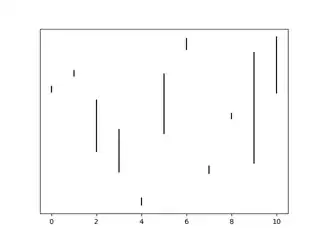
Geometric version of the problem

And its solution:

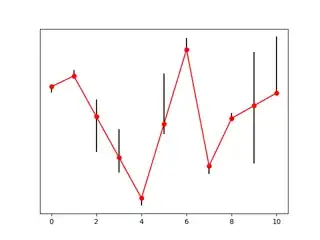
Optimal solution

The algorithm

The idea of the algorithm is to find where the next bend is going to be, and restart from there. Knowing the previous bend, we maintain the minimum and maximum slope for the next line, and which $i$ is at the limit, until we are forced to introduce a new bend.

So the core loop is:

def find_next_bend(n, l, u, x, previous_bend):
    min_slope = -float("inf")
    max_slope = float("inf")
    min_slope_ind = -1
    max_slope_ind = -1
    for i in range(last_bend+1, n):
        new_min_slope = (l[i] - x[previous_bend]) / (i-previous_bend)
        new_max_slope = (u[i] - x[previous_bend]) / (i-previous_bend)
        if new_min_slope > max_slope:
            # Bend upwards
            x[max_slope_ind] = u[max_slope_ind]
            return max_slope_ind
        if new_max_slope < min_slope:
            # Bend downwards
            x[min_slope_ind] = l[min_slope_ind]
            return min_slope_ind
        if new_max_slope < max_slope:
            # Restrict max possible slope
            max_slope_ind = i
            max_slope = new_max_slope
        if new_min_slope > min_slope:
            # Restrict min possible slope
            min_slope_ind = i
            min_slope = new_min_slope

There are cornercases for the first and last bend, that I won't describe here: they are commented in the full code. The proof of the algorithm is left as an exercise for the reader :)

Computational results

The algorithm scales perfectly on random data, and finds the optimal solution for $n > 10^6$ in seconds. Theoretically, it is only $O(n^2)$ as far as I can tell, but has linear complexity in practice. I am convinced that it's possible to find something that is $O(n \log n)$, as it bears some similarity to 2D convex hull algorithms, but that's fun for another day ;)

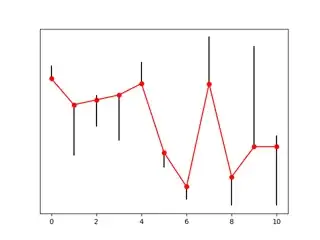
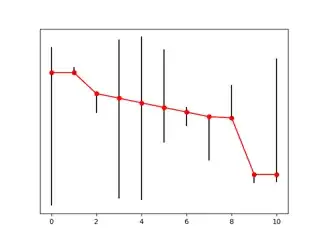
First exampleSecond example Third exampleFourth example

Ggouvine
  • 1,877
  • 7
  • 13
  • 1
    Could you explain how OPs formulation can be translated to your geometrical problem ? Looks interesting! – Kuifje Nov 25 '20 at 19:38
  • This is a neat way to think about it! Could you give a bit more detail of the rough outline of the algorithm? I'm sure I could decipher your Python (though it's not a language I use), but some pseudo code here may be more generally accessible. – cfp Nov 25 '20 at 20:49
  • 1
    Thanks! I don't have much time right now, but I'll try detailing it tomorrow. I think the easiest way to see the equivalence of the formulations despite the different objective function is to look at the optimality conditions: in both cases, they are $x_i - x_{i-1} = x_{i+1} - x_i$ if $x_i$ is not at its bound, and $x_i - x_{i-1} \gt x_{i+1} - x_i$ or $x_i - x_{i-1} \lt x_{i+1} - x_i$ depending on the bound otherwise. – Ggouvine Nov 25 '20 at 20:59
  • 2
    I just added some code and the above explanation in the answer. For the full algorithm, you will still have to look at the full Python code: I don't want to detail the cornercases in the answer, since they are not interesting and make the algorithm quite long. – Ggouvine Nov 26 '20 at 11:33
  • Very elegant, both interpretation and solution, Gabriel ;-) Here is a QP which looks like hard at a first glance but in effect easy :-) Seems also that the integer version is as easy as the continuous one. The challenge is indeed to solve it in O(n log n) time. – Hexaly Nov 26 '20 at 19:33
  • 2
    Thank you :-) If only all QP were like this :D I'd like to see someone come up with an O(n log n) algorithm, too! – Ggouvine Nov 28 '20 at 09:29
  • Shouldn't it be "if new_max_slope <= max_slope" (<= not <)? An edge case of course, but potentially important. – cfp Dec 02 '20 at 14:31
  • 1
    Both are equivalent here. <= would report one more bend while it's just a straight line, but would be correct. – Ggouvine Dec 02 '20 at 15:02
  • 1
    A Matlab version of your code is here: https://gist.github.com/tholden/54fbcda21dc8698eceeefde0f2e205fb – cfp Dec 02 '20 at 16:36