2

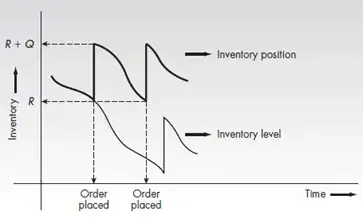
I have previously asked this problem here-Lead time longer than cycle time, but I keep getting more confused the more I think about it. Using the Q,R inventory model, suppose my mean monthly demand $\mu = 4000, \sigma_D = 1500$, Order quantity $Q = 6000$ and lead time $L = 3$(months). Choosing $\alpha = 2.33$, I get $SS \approx 6000$ and $ROP \approx 18000$. ROP is interpreted as the inventory position here. The values seem reasonable enough.

Now suppose I take $L = 10$, the safety stock value shoots up to $SS = 11,000$ and $ROP = 51,000$ This definitely seems absurdly high to me. I don't get why we use the lead time as it is in the formula because at a steady-state, and assuming the demands are normally distributed, we will be receiving an order every $Q/\mu = 6000/4000 = 1.5$ months on an average. Why, then, does the formula say that we need to use the lead time L = 10, when we know that the inventory would be replenished much before that? In my opinion, we only need to cover-up for fluctuations in demand in that 1.5 month period. I couldn't find any text that clearly explains this dichotomy between Inventory Position and Inventory Level and any help is appreciated.

EDIT:Inventory Position and Levels

Nishant Kumar Gupta
  • 401
  • 2
  • 9

1 Answers1

1

You seem to be conflating two ordering systems. You say you will be receiving an order every 1.5 months on average. The only way that could happen with a lead time of 10 months would be if you had more than one order outstanding at a time. This ties to your use of $Q=6,000$ in the second paragraph. That's the order quantity when $L=3$, not when $L=10$. So if you are going to stick to an ROP/ROQ system (order when you hit the ROP, then not again until after that order arrives), you'll order $Q=40,000$ units, which is 10 months of demand. If, instead, you decide to stick with $Q=6,000$, you're moving from an ROP system to what looks more like an EOQ system ... or at least you'll be ordering at more than one reorder point.

prubin
  • 39,078
  • 3
  • 37
  • 104
  • Yes, there would be several outstanding orders with a lead time of 10 months. I have added a picture to give more clarity. You can see that 2 orders have been placed even before the first one arrives (because the Inventory Position dropped to the ROP twice). My demands are still stochastic so I am not sure how it behaves more like an EOQ system? – Nishant Kumar Gupta Jun 08 '20 at 06:02
  • How did the inventory position go up before an order arrived? – prubin Jun 08 '20 at 15:09
  • That's how it is, isn't it? Inventory position is interpreted as on-hand inventory + outstanding orders - backorders. So if I have 6,000 units on hand and outstanding orders of 12,000 units, my inventory position will be 18,000 units. That's why the IP goes up when we place an order but the IL (on-hand levels) stay the same until an order actually arrives – Nishant Kumar Gupta Jun 08 '20 at 15:53