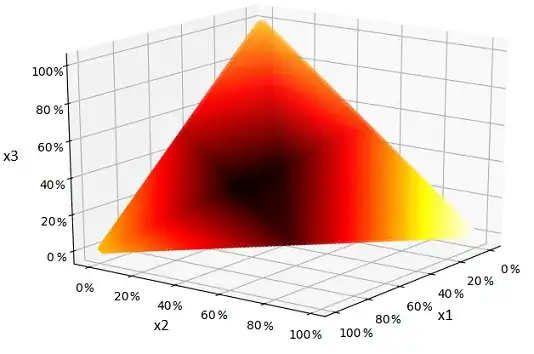
First, the problem is not a linear optimization problem, at least not for the objective function shown (which is nonlinear due the conditional portion in lines 10-13 and particularly the division by E_ges_i in line 13. Simulated annealing might be fine as a heuristic approach, but given the nonlinear objective, only accepting improving steps might or might not be appropriate. If the objective is unimodal, I think skipping steps that make the objective worse might be okay. Then again, if the heat map is unimodal, constrained gradient descent might work just as well or better.
Sticking to the objective function shown, another possibility would be to treat the problem as a mixed integer linear program, using a piecewise linear approximation to the objective function. Since an approximation is involved, you might want to try gradient descent or other local search from the model's solution to see if you can improve it, or alternatively refine the approximation near the model solution and solve the revised model (ad nauseum).
ADDENDUM: I just hacked a little R code, using the objective function posted on GitHub. The algorithm I used is the Nelder-Mead polytope algorithm, as described in 1. The Nelder-Mead algorithm, published in 1965, was a modification of an earlier algorithm (by Spendley, Hext and Himsworth in 1962, according to 1) and has likely been improved upon in turn since the '60s. The attraction of the Nelder-Mead algorithm (or its relatives) here is that it starts with a simplex as the search region and progressively shrinks to smaller and smaller simplices, all of which are subsets of the original. So if we use N-M starting with the unit simplex, the constraints are always satisfied.
I did not put in much care in the coding, did not code all the possible adjustments (such as random restarts), and picked the expansion, contraction and reflection parameters out of thin air. That said, it converged (or at least stopped) after seven iterations on the test problem, with a solution of (0.0126960, 0.2461336, 0.7411704) and an objective value of -4675913 -- not optimal, but I think not too shabby (particularly since I did not code restarts or other more recent tweaks to Nelder-Mead). It's not hard to code, and it does not require derivatives, just function evaluations.
1 P. Gill, W. Murray and M. Wright, Practical Optimization (Academic Press, 1981).
ADDENDUM 2 I updated my R code to use the simplified version of the cost function from the GitHub repository (which is a bit better behaved when an argument is zero). I also switched from the Nelder-Mead algorithm as present in Gill, Murray and Wright to the version on the Wikipedia page, and adjusted the parameter values to the ones they recommend. I have to qualify my earlier comment about Nelder-Mead automatically maintaining feasibility. The condition that the weights sum to 1 is automatically maintained. Nonnegativity of the weights requires occasionally shrink a proposed step, which is easily handled.
With the modified code and the parameter values from the Wikipedia page, I get a final solution of (0, 0.2885719, 0.7114281) with an objective value of -4,683,095.
ADDENDUM 3 Hopefully this will be my final addendum. :-) I also tried a genetic algorithm (in R). The solution from a GA is inherently random, but with the parameters and random seed that I chose I got a final solution of (0.001182725, 0.2869361, 0.7118812) with objective value -4,683,175, which is slightly better than both what I got with Nelder-Mead and what LocalSolver reported.
My R code for both Nelder-Mead and the GA (using the genalg R library) are available in an R notebook.
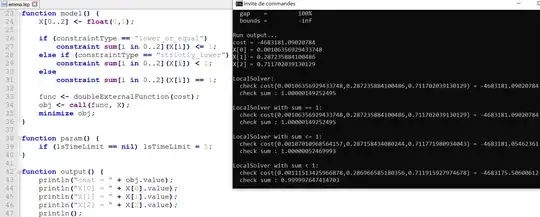
if C_ges > E_ges. Is it possible to rewrite the cost function without the conditional? This kind of discontinuity will cause you pain. Where are you getting your cost functions from/what do they mean? – Richard May 28 '20 at 17:36min(C_i, e) * (P_i - v)ase * (P_i - v)with the constraint thate<=C_i. This gets you close to having a quadratic program, which you can solve efficiently and exactly. However, looking at the values ofC[i]in your example and the constraint thatx>=0, it will always be the case thatmin(C_i,e)=C_i. Are you sure this objective function is correct? – Richard May 29 '20 at 06:34-C_i, you're right. I have edited it, but apart from that I get the same results for the simplification as for the old objective function, so it should be correct. Does this help us? – Emma May 29 '20 at 14:18