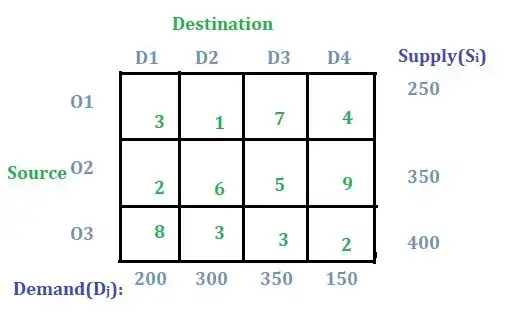
In a simple transportation problem like below image, how to model a constraint for shipment discount e.g. if quantity transported from any origin to any destination is more than 100 unit then the supplier will offer 10% discount in the cost of transportation or if quantity transported from any origin to any destination is more than 200 then the supplier will offer 20% discount in the cost of transportation?
There are many ways to do this. Here is one. In what follows, $x=x_{ij}$ where $(i,j)$ is a given edge (in other words it is only valid for one edge). You have to apply the same technique for the rest of them.
So your cost function is of the form $$f(x) = \left\{\begin{matrix} cx, & 0 \le x < 100\\ 90\%\;cx, & 100 \le x < 200\\ 80\%\;cx, & 200 \le x < 300 \end{matrix}\right.$$
You can write the objective function as $$ f(x_1,x_2,x_3)=cx_1 +90\%\;cx_2+80\%\;cx_3 $$ with constraints $$0 \le x_1 \le 100y_1$$ $$100y_2 \le x_2 \le 200y_2$$ $$200y_3 \le x_3 \le 300y_3$$ $$y_1+y_2+y_3=1$$ $$y_1, y_2, y_3 \in \{0,1\}$$ $$x_1,x_2,x_3 \ge 0$$
