5

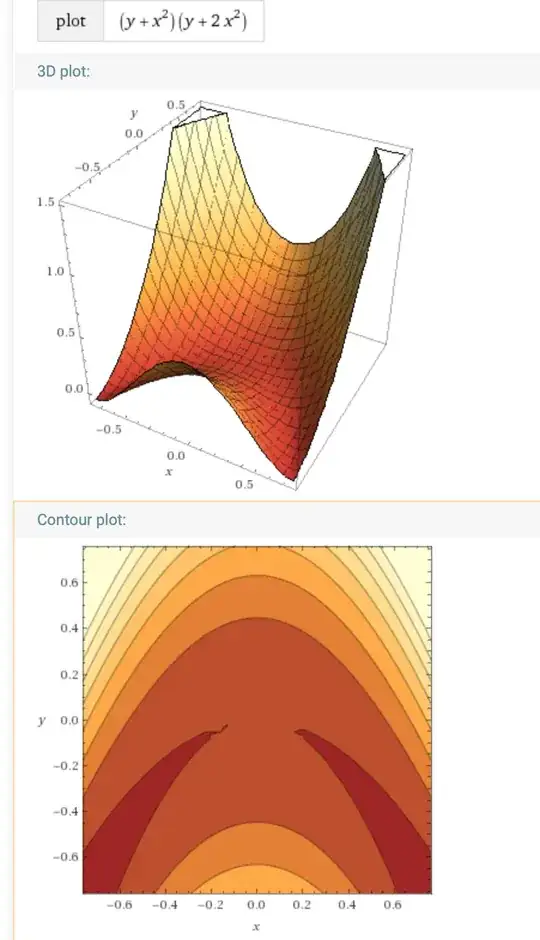
Let $f:\mathbb{R}^n \mapsto \mathbb{R}$ be a differentiable function. Suppose $x^*$ is a local minimizer of $f$ along every line that passes through $x^*$. This means that the function $$g(\alpha) = f(x^* + \alpha d)$$ is being minimized for $\alpha = 0$ for any direction $d \in \mathbb{R}^n$. It is easy to show that this implies $\nabla f(x^*) = 0$.

The question is:

Is $x^*$ a local minimizer of $f$?

The answer is, it can be a local minimizer, maximizer, or a saddle point. I really don't get the reason. We are given that, for sufficiently small $\alpha>0$, $f(x^*) \leq f(x^* + \alpha d), \forall d \in \mathbb{R}^n$. Doesn't this also imply that $x^*$ is a local minimizer?

independentvariable
  • 3,980
  • 10
  • 36

1 Answers1

6

Here is a counterexample:

Consider $n=2$, $f(x,y)=(y+x^2)(y+2x^2)$ where and consider $(x^*, y^*)=(0,0)$.

\begin{align}g_d(\alpha)&=f(\alpha d_1, \alpha d_2)\\&= (\alpha d_2 + (\alpha d_1)^2)(\alpha d_2 + 2(\alpha d_1)^2)\\ &= \alpha^2(d_2+\alpha d_1^2)(d_2+2\alpha d_1^2)\\ &= \alpha^2(2d_1^4\alpha^2 + 3d_2d_1^2\alpha+d_2^2) \end{align}

We know that $g_d(0)=0$, let's study what happens when $\alpha \ne 0$.

If $d_2=0$, then we have $g_d(\alpha ) \ge 0$.

If $d_2 \ne 0$, note that $2d_1^4\alpha^2 + 3d_2d_1^2\alpha + d_2^2>0$ when $\alpha$ is small but non-zero, hence $g_d(\alpha)\ge 0$ near the zero neighborhood.

Hence $(0,0)$ is a local minimizer of $f$ along every line.

However,

$$f\left(x, -\frac32x^2\right) = \left(-\frac32x^2+x^2\right) \left(-\frac32x^2+2x^2\right)=-\frac14x^4\le 0$$

In particular, we can let $x$ be arbitarily small and non-zero.

Hence $(0,0)$ is not a local minimum.

enter image description here

Community
  • 1
Siong Thye Goh
  • 912
  • 1
  • 8
  • 17
  • Thanks for your answer! I also have a counter-example: $f(x_1, x_2) = (x_2 - x_1)^2(x_2 - 2x_1^2)$. However, I don't get the intuition. Can you please help me with the intuition? – independentvariable Apr 20 '20 at 14:15
  • I think counterexamples illustrate that even though we restrict it to a line, a point is a minimum along the restricton. However, if we draw a neighborhood, and draw a certain small curve, we can find a smaller value. – Siong Thye Goh Apr 20 '20 at 14:18
  • That's very hard to imagine... I always think like if $x^$ is the minimum over each line, then it is local minimum, because any point in the very-small-ball around $x^$ also is on a line from $x^*$. – independentvariable Apr 20 '20 at 14:28
  • 1
    not sure if a desmos link would help. – Siong Thye Goh Apr 20 '20 at 14:37
  • Thank you very much! – independentvariable Apr 20 '20 at 14:40
  • 1
    I think part of the intuition is that, in your statement about "sufficiently small $\alpha > 0$, the "sufficiently small" part is different for each direction. So for any given $\alpha$, there's a direction in which it is not small enough to prevent a decrease in $f$. – prubin Apr 20 '20 at 16:07
  • @prubin This actually concluded my question. Thanks for that. It is very hard to imagine visually :) – independentvariable Apr 20 '20 at 16:09