Job Shop Scheduling: what objectives are harder?

Question

It is well known that job shop scheduling problems are notoriously hard from a computational point of view. Many papers exist for the makespan objective, and some report on min sum objectives (like minimize weighted completion time, minimize earliness/tardiness penalties etc).

My question: does anyone know whether makespan or min sum objectives are computationally more difficult when using MILP approaches?

Not directly answering your question, but I believe that such objectives are generally hard for polyhedral approaches such as MILP. My guess is that, since the resource constraints on JSPs are disjunctive in nature, it makes it somewhat unavoidable to use using big M variables in MILP formulations. Ever in literature, we often find CP approaches fare better than MILP approaches for obtaining the optimal solution of JSPs. — batwing, Jan 23 '20 at 18:06
Thanks, I usually use "configuration" based formulations (that are solved by branch-and-price), so I can avoid the big $M$. But you are right, of course, MILP is not very suited -- yet, this is exactly what I am interested in (I edit my post, thanks!). — Marco Lübbecke, Jan 23 '20 at 18:33
To add @batwing mentioned, MILPs may not be the best choice to formulate JSPs, specifically in real situations, hence using the CP approach or resource decomposition-based methods like shift bottleneck heuristic would be interested. — A.Omidi, Jan 23 '20 at 20:00
Thanks, I know. But, really, I am specifically interested in MILP, and specifically in these two objective functions :) — Marco Lübbecke, Jan 23 '20 at 20:03
@marco Lubbecke, I'm wondering if you could explain about the configuration-based formulation to use branch and price method or if you know any document about that. (specific in JSPs scheduling.) — A.Omidi, Jan 23 '20 at 20:09
for branch-and-price, there are e.g., papers by Lancia et al., Pessoa et al., Sadykov et al., which sometimes "only" solve the Lagrangian relaxation, but the models are the same. And I have a paper with a co-author, which is unpublished, and which is why I am asking :) — Marco Lübbecke, Jan 23 '20 at 20:19
It seems that for the decision problem it can be shown that the total lateness objective is at least as general as the makespan objective: Assume we want to know if there exists a schedule with a makespan of at most M. When setting the due dates of all jobs to M, a schedule with a makespan of at most M exists if there is a schedule with a total lateness of zero. I don't see such a reduction for the other direction. — SebastianK, Jan 24 '20 at 15:23
Another indicator why min sum objectives are computationally more difficult is that the makespan depends only on the completion time of the latest job, whereas for min sum objectives the completion times of all jobs might have an influence. — SebastianK, Jan 24 '20 at 15:23
@SebastianK, would you like to turn your comments into an answer? this is the best we have so far... — Marco Lübbecke, Jan 29 '20 at 12:05
@MarcoLübbecke Thank you for suggesting this. I posted an answer based on the comments. — SebastianK, Feb 02 '20 at 18:25
Could you show the log of a MILP solver solving an instance with each objective? — fontanf, Mar 15 '23 at 15:30

SebastianK · Accepted Answer · 2020-02-02T18:30:33.613

Some observations why min sum objectives are computationally more difficult than the makespan objective:

For the decision problem, it can be shown that the total lateness objective is at least as general as the makespan objective: Assume we want to know if there exists a schedule with a makespan of at most $M$. When setting the due dates of all jobs to $M$, a schedule with a makespan of at most $M$ exists if there is a schedule with a total lateness of zero. I don't see such a reduction for the other direction.
Another indicator why min sum objectives are computationally more difficult is that the makespan depends only on the completion time of the latest job, whereas for min sum objectives the completion times of all jobs might have an influence. This is related to the following. In heuristics, solutions of are often represented using conjunctive graphs. In order to efficiently evaluate moves, one can estimate the impact of a move to the objective function instead of actually executing the move. Estimating the impact of a move is less complicated for the makespan in comparison to other regular criteria (such as the min sum objectives).

score 2 · Answer 2 · answered Mar 15 '23 at 13:39

In addition to the above answer, the following might be worthwhile too.

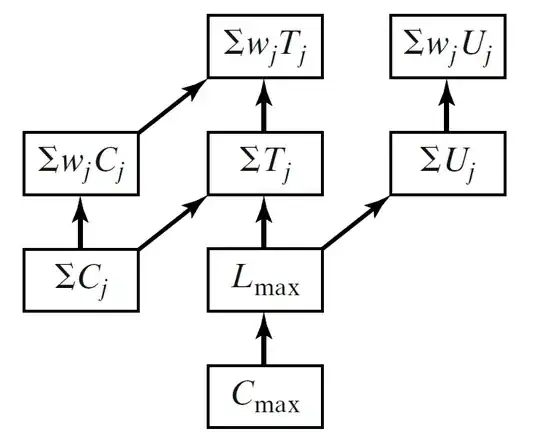
Often, an algorithm for one scheduling problem can be applied to another scheduling problem as well. For example, $ 1|| \sum c_{j} $ is a special case of $ 1|| \sum w_{j}c_{j} $ and a procedure for this can also be used for the first one. In complexity terms, it is said that $ 1|| \sum c_{j} $ reduces to $ 1|| \sum w_{j}c_{j} $. Based on this concept a chain of reductions can be established. For example:

$$ (1|| \sum c_{j}) \rightarrow (1|| \sum w_{j}c_{j}) \rightarrow (P_{m} || \sum w_{j}c_{j}) \rightarrow (Q_{m} |prec| \sum w_{j}c_{j}))$$

As an example of hard and easy problem, $ 1 || C_{max} $, $ P_{2} || C_{max} $, $ F_{2} || C_{max} $, $ J_{m} || C_{max} $, and $ FF_{c} || C_{max} $:

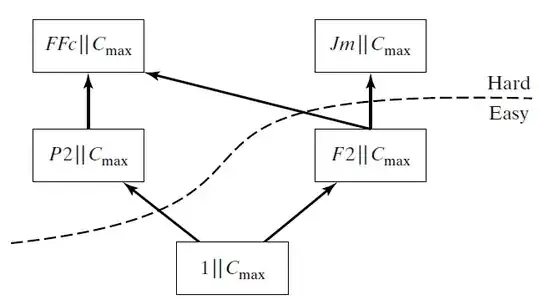
Of course, there are also many problems that are not comparable with one another. For example, $ P_{m} || \sum w_{j}T_{j}$ is not comparable to $ J_{m}|| C_{max} $.

A considerable effort has been made to establish a problem hierarchy describing the relationships between the hundreds of scheduling problems. In the comparisons between the complexities of the different scheduling problems, it is of interest to know how a change in a single element in the classification of a problem affects its complexity. The following graph helps determine the complexity hierarchy of deterministic scheduling problems based on the different objective functions.

Job Shop Scheduling: what objectives are harder?

2 Answers2

Linked