Count this to the family of Job Shop Problem?

Question

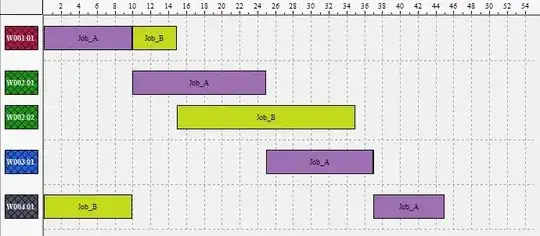
I will explain the problem in a simplified version.

• Three Tasks: $T_1, T_2, T_3$

• Four Machines: $M_1, M_2, M_3, M_4$

The machines $M_2$ and $M_3$ make the same processing, so they are parallel.

Tasks $T_1$ and $T_3$ must go through the machines in the following order: $M_1 \to (M_2\, or\, M3) \to M_4$.

Task $T_2$ is different, not all machines need to be run through. The order is $M_1\to M_4$.

My question is now if this counts to the family of job-shop problems? Because in books I always read that in the job-shop problem every task must be processed on every machine, but the order does not matter.

If this is not a job-shop problem, to which family of the shop problems does this explanation count? It would be very helpful if you can add the book/paper where this is defined, that I can obtain more info about it?

Answer 1

As per you have a specific route for each job, it sounds like a flexible job shop problem. In a practical situation, many times, a specific job maybe does not need to process in all stages.

For example, we have two jobs (A and B) and four stages. Job A should be processed in all four stages while job B need to be processed in the three stages.

if you are willing to learn more about job shop models, the following links would be useful.

• What is the difference between job shop scheduling and resource constrained project scheduling?
• What class of scheduling problem models jobs which require multiple machines simultaneously?

Indeed, a good reference is:

• Planning and Scheduling in Manufacturing and Services by Michael Pinedo