11

We're working on a facility location problem in which it is desirable for the facilities to be laid out as close as possible to a grid. In our problem, a lattice is overlaid on the region, and the centers of the resulting cells are potential facility locations.

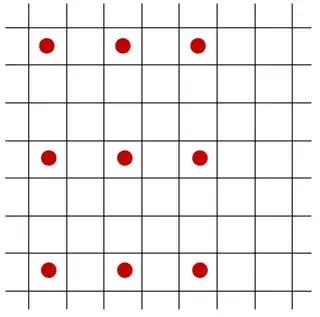
We want the facilities to be in a regular pattern that resembles a grid. So, it is preferable to have a layout like this:

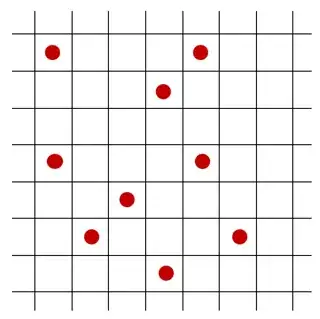
enter image description here

rather than one like this:

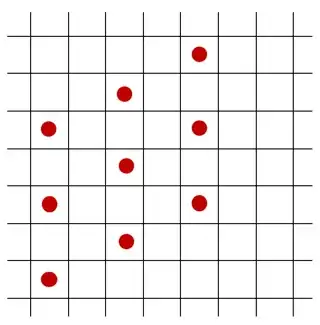
enter image description here

Note that the grid does not have to be the same as the lattice; that is, the following is good too:

enter image description here

Is there a way to evaluate how close a given set of points lies to a grid? (i.e., the "griddiness" of the set of points)

In particular, I'm looking for either a simple calculation (something involving sines and cosines...?) or an efficient algorithm that will give a score indicating how "griddy" a set of points is. Most likely we'll be using this within a heuristic (greedy + swap, metaheuristic, something like that), but bonus points if there's a method that could be incorporated into a linear MIP.

Note that we don't know in advance which "grid" the solution will resemble -- the method should be capable of determining that both the first and the third layouts are good, and the second is bad.

LarrySnyder610
  • 13,141
  • 3
  • 41
  • 105

2 Answers2

8

An idea could be to evaluate what is the smallest number of straight lines required to cover your locations. You would expect that aligned points are covered with much fewer straight lines than non-aligned points. Moreover, this metric would work for any type of alignment, not just the one that follows the lattice.

This paper (Covering a set of points with a minimum number of lines, by Grantson and Levcopoulos) seems to suggest that the evaluation of such a term in the objective function should not be too expensive.

Alberto Santini
  • 2,113
  • 9
  • 23
  • That is a great idea. The one problem I can see is that if a point is slightly off the grid, I'd like it to count as "close but not on," whereas requiring every point to be on a line would force a new line through that close-but-not-griddy point. But maybe the approach in that paper can be modified to allow a line to "cover" a point if it is close but not on it. – LarrySnyder610 May 31 '19 at 11:58
  • By the way, the link you provided gives me a captcha-type prompt in Russian...I gave up. But this is the link to the paper on Springer's web site. – LarrySnyder610 May 31 '19 at 11:58
  • You could try to cover with stripes of suitable width. If that's too hard, you could do this greedily: find the stripe that cover most points, and remove those points; repeat until no points are left. It's a heuristic, but you want to embed it into a heuristic in any case. – Alberto Santini May 31 '19 at 13:48
  • @LarrySnyder610 yes, the paper should be after the captcha. I tried to avoid linking to the pay-walled version. :-) – Alberto Santini May 31 '19 at 13:49
  • I see. I thought it looked a little spammy so I fled. :) – LarrySnyder610 May 31 '19 at 13:50
  • 1
    @LarrySnyder610 This paper may also provide some general idea on the approach: – EhsanK May 31 '19 at 13:54
  • Larry, the captcha is simply the numbers in the image (don't worry about what the button says, it simply offers new numbers if you can't read the image). Alberto, your link is not loading (nothing shows up, and it's not 404), would you fix it please. – Rob Aug 01 '19 at 19:59
6

This is interesting. Perhaps you could find the linear transformation to the lattice that has the minimum deviation from integrality. This would "standardize" your grid in some sense.

That might look something like the following (haven't tried it):

Sets: ($M$: locations; $N$: dimension of data)

Variables: ($a$: transformation multipliers, $y$: projected point; $z$: closest integer point, $\epsilon$: deviation from integer point)

Data: ($x$: your original points)

Formulation:

\begin{array}{ll} \min_{a,y,z,\epsilon} & \sum_{m\in M}\sum_{n\in N}\epsilon^{m+}_n+\epsilon^{m-}_n\\ \text{subject to} & a_nx_n^{m} = y_n^{m}, & \forall m \in M, n\in N\\ & y_n^{m} + \epsilon_n^{m+}-\epsilon_n^{m-} = z_n^m, & \forall m \in M, n\in N\\ &z_n^m \in \mathbb{Z}, & \forall m\in M, n \in N\\ & a_n \in \mathbb{R}, & \forall n \in N\\ & y_n^m \in \mathbb{R}, &\forall m\in M, n\in N \\ &\epsilon_n^{m+} ,\epsilon_n^{m-} \geq0, & \forall m\in M, n \in N \end{array}

The objective function (OF) of a given set of points (the $x$'s) could be compared to the OF with a different set of points ($x_{alt}$) as long as the dimensions are the same.

One downside is that this wouldn't handle "holes" in the grid well - if your data is equally spaced but in an L, this would give the same result as having them all in a square. Not sure if that matters for your application. Similarly, this wouldn't penalize locations that are increasing in distance from each other in constant increments (e.g., in one dimension a spacing of 1 2 4 8 would be the same as 1 2 3 4).

Also this is a mixed-integer LP when the points are fixed, but if they're variables as well, this becomes nonlinear.

E. Tucker
  • 1,317
  • 8
  • 22