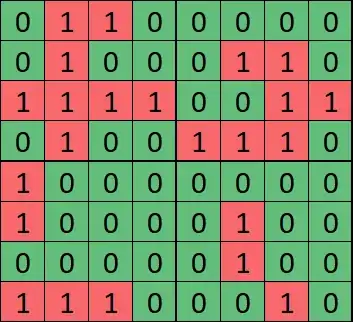
Setup
I have a binary $N \times N$ matrix. The objective is to minimize the number of ones in the matrix, subject to various constraints. This leads to symmetries by rotating 90 degrees and/or mirroring (along the axis and diagonals). Here's an example:
Given the objective function, this matrix has the same objective value as a rotated or mirrored copy of the same matrix. The model performance improves if I add symmetry-breaking constraints, especially on infeasible instances. I sum the quadrants the following way and generate symmetry-breaking constraints:
- To account for rotations and mirroring:
- $ q_1 \geq q_2 $ (A1)
- $ q_1 \geq q_3 $ (A2)
- $ q_1 \geq q_4 $ (A3)
- To account for diagonal mirroring:
- $ q_2 \geq q_3 $ (B1)
Question
Are there more efficient/simpler alternatives to state the symmetry-breaking constraints, for example with fewer non-zero coefficients?