Algorithm needed to find optimum area of 2-dimensional data set

Question

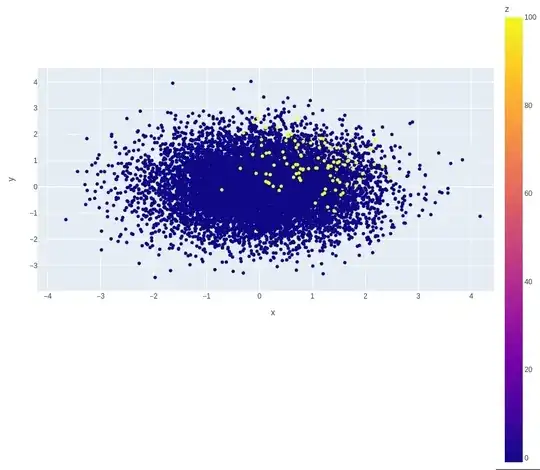
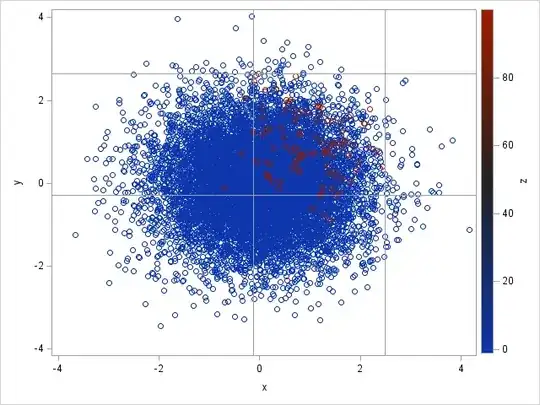
The python script depicted below generates the following toy data set.

I need to determine the values for $x_{min}$, $x_{max}$, $y_{min}$, $y_{max}$ describing a rectangular area where the sum over all $z$s in that area is maximized. In other words: which area is the best compromise between negative values of $z$ and positive $z$ values.

What would be the best approach to achieve this?

Would it make sense to start with the whole area and then make the rectangular box smaller with each iteration? E.g. take away a fraction of the area on the left side, then on the top, the right, and the bottom. Whenever the sum over all $z$s is increased, that step was successful. Once a step does not increase the sum over all $z$s for that box, this step should not be executed but omitted (variant a). Or the fraction with which the area was reduced should be set smaller (variant b).

Would such an approach make sense?

If somebody has an alternative idea: I am glad for any input.

If somebody is even able to supply any coding hints/solutions, such input is very welcome, too.

The code:

import numpy as np
import pandas as pd
import plotly.express as px
np.random.seed(1)
configuration for first array
mean0 = np.array([0., 0.])
cov0 = np.array([[1., 0.], [0., 1.]])
size0 = 10000
configuration for second array
mean1 = np.array([1., 1.])
cov1 = np.array([[.5, 0.], [0., .5]])
size1 = 100
build first array
vals0 = np.random.multivariate_normal(mean0, cov0, size0)
append another column to the right of the array
vals0 = np.append(vals0, [[-1] for x in range(size0)], axis=1)
fill new column with randomized data (negative values)
vals0[:, 2] = -1.0 + 0.2 * np.random.random(size0)
build second array
vals1 = np.random.multivariate_normal(mean1, cov1, size1)
append another column to the right of the array
vals1 = np.append(vals1, [[-1] for x in range(size1)], axis=1)
fill new column with randomized data (positive values)
vals1[:, 2] = 100.0 - 0.2 * np.random.random(size1)
combine first and second array
vals2 = np.append(vals0, vals1, axis=0)
convert numpy array to pandas DataFrame
df = pd.DataFrame(vals2, columns=['x', 'y', 'z'])
use plotly to visualize the data
fig = px.scatter_matrix(df.sort_values('z'),
                        dimensions=["x", "y"],
                        color="z")
do not show diagonal data
fig.update_traces(diagonal_visible=False)
fig.show()

Answer 1

Expressed via Iverson bracket notation, your problem is to maximize $$\sum_i z_i [x_\min \le x_i \le x_\max][y_\min \le y_i \le y_\max].$$

You can linearize the problem as follows. Introduce five binary decision variables for each point:

• $s_i$ indicates whether point $i$ is selected
• $\ell_i$ indicates whether point $i$ lies to the left of $x_\min$
• $r_i$ indicates whether point $i$ lies to the right of $x_\max$
• $b_i$ indicates whether point $i$ lies below $y_\min$
• $a_i$ indicates whether point $i$ lies above $y_\max$

Now maximize $\sum_i z_i s_i$ subject to \begin{align} s_i + \ell_i &+ r_i + b_i + a_i \ge 1 \\ s_i = 1 &\implies x_\min \le x_i \\ s_i = 1 &\implies x_i \le x_\max \\ s_i = 1 &\implies y_\min \le y_i \\ s_i = 1 &\implies y_i \le y_\max \\ \ell_i = 1 &\implies x_\min \ge x_i \\ r_i = 1 &\implies x_i \ge x_\max \\ b_i = 1 &\implies y_\min \ge y_i \\ a_i = 1 &\implies y_i \ge y_\max \end{align} (These last four are really $>$, which you can approximate with $\ge \epsilon +$ for some small positive constant tolerance $\epsilon$ or make exact by using the "neighboring" $x_j$ or $y_j$ value.)

If your solver does not support indicator constraints, you can linearize via big-M. For example, $x_\min - x_i \le M_i (1-s_i)$ enforces $s_i = 1 \implies x_\min \le x_i$.

An optimal solution turns out to be $$x_\min = -0.12689, x_\max = 2.4819, y_\min = -0.29736, y_\max = 2.6423,$$ with optimal objective value $6332.619425$.

Answer 2

Let's say that $\hat{x}_1 \lt \cdots \lt \hat{x}_M$ are the distinct values of $x$ in the data, sorted into ascending order, and similarly $\hat{y}_1 < \cdots \lt \hat{y}_N$ are the sorted distinct values of $y.$ Without loss of generality we can focus on boxes where each of the four edges contains at least one point. For your "shrink the box" approach, if you are bringing the left side in and the left side contains one or more points with $x=\hat{x}_i,$ then you can increase the $x$ value of the left side to $\hat{x}_{i + 1},$ and similarly for moving the other three edges inward.

Answer 3

If you care about performance, I think it makes more sense to implement this in custom code rather than try to solve it with a solver. There is a straightforward algorithm. Let $x_1<\dots<x_m$ denote the distinct values of $x$ in the data, and $y_1<\dots<y_n$ the distinct values of $y$ in the data. Then we can use the following algorithm:

• For each $i:=1,2,\dots,m-1$:

  • For each $i':=i+1,\dots,m$:

    • For each $j:=1,2,\dots,n$:

      • For each $j':=j+1,\dots,n$:

        • Compute the total $z$-value of all points in the box $[x_i,x_{i'}] \times [y_j,y_{j'}]$. Remember the best seen so far.

The running time of this naive algorithm will be $O(m^2n^2N)$, where $N$ counts the number of data points.

You can speed up the algorithm by using standard data structures for storing data in the plane, such as a 2-dimensional k-d tree or a quadtree. Augment each node in the tree with the sum of all $z$-values of points that fall within the rectangular region corresponding to that node. Then, you can compute the total $z$-value of all points in the box $[x_i,x_{i'}] \times [y_j,y_{j'}]$ by expressing it as the sum of some disjoint rectangles, each rectangle corresponding to a node in the tree. Heuristically, we can expect each box to be decomposed into something like $O(\log N)$ different rectangles.

Therefore, with this improved data structure, I expect the running time will be improved to something like $O(m^2n^2\log N)$.

I am not aware of any algorithm that is guaranteed to give the correct answer and is faster than these algorithms (including the ones listed in other answers; solvers don't have any magic sauce that will speed this up).