Traffic lights optimization

Question

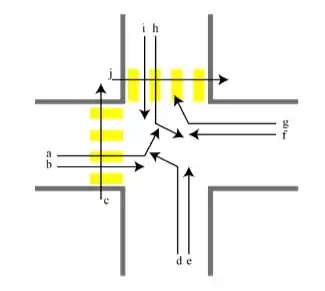
I am interested in the following problem dealing with the optimization of traffic lights on the intersection illustrated below:

The goal is maximize the duration during which each movement $m\in M=\{a,...,j\}$ has a green light, subject to the following constraints:

• incompatible movements cannot be done simultaneously
• each movement has to have a green light for at least $s$ seconds
• the duration of a complete cycle must equal $C$ seconds

One strategy is to:

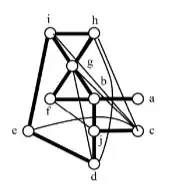
1. Consider the compatibility graph $G=(V,E)$ (an edge exists between two movements if they can be done simultaneously):

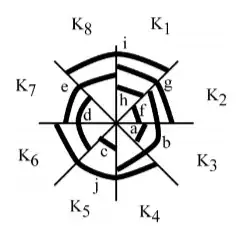
2. Find a vertex cover of cliques (sets of pairwise compatible movements) ordered in a circular fashion:

3. Solve the following linear program: let $t_i$ be a continuous variable representing duration of green light for clique $K_i$, and maximize $\sum_{m\in M}\sum_{i|m\in K_i} t_i$ subject to $\left\{\sum_i t_i=C,\sum_{i|m\in K_i} t_i \ge s \; \forall m\in M \right\}$.

I find Step 2 (order the maximal cliques in a circular fasion) to be a bit tedious and am trying to figure out a (mixed integer) linear formulation for this problem. Any suggestions are welcome.

Answer 1

If a movement belongs to $c$ cliques, then you want $c-1$ of those cliques to be followed by another clique from the same set.

Let $k$ be the number of cliques and let $H_m=\lbrace i : m\in K_i\rbrace$ for all movements $m\in M.$ Define binary variables $z_{ij}$ for all pairs of clique indices $i\neq j,$ where $z_{ij}=1$ will signal that clique $j$ follows clique $i$ in a clockwise traversal of your circle. Fix $z_{ii}=0$ for all $i$ (to simplify the indexing in what follows) and dd the constraints $$\sum_{i=1}^k z_{ij} = 1\quad \forall j\in \lbrace 1,\dots, k\rbrace$$ and $$\sum_{j=1}^k z_{ij} = 1\quad \forall i\in \lbrace 1,\dots, k\rbrace$$ to ensure that every clique is preceded/followed by exactly one clique.

Now for each movement $m$ add the constraint $$\sum_{i,j\in H_m : i < j} ( z_{ij} + z_{ji}) \ge \vert H_m \vert - 1.$$ This says that the total number of transitions between cliques containing $m$ has to be at least the number of such cliques minus 1, or equivalently that the number of times in a cycle you transition from a clique containing $m$ to a clique not containing $m$ is at most 1. (I used $\ge$ rather than $=$ in case you might have a movement permissible throughout the entire cycle of the light.)

Answer 2

I'd try by defining binary variables $ x$ indexed on set of compatible edges $E$ & time $t$ over set $C$. Also define a set of edges, F where simultaneous movement is possible. Then add constraints like:
$ sx_{\epsilon,t-1} - \sum_{k=1}^{t-2}x_{\epsilon,k} \le sx_{\epsilon,t} \quad \forall \epsilon \in E \ \ \forall t$: ensures contiguous allocation of $\ge s$ secs

$ \sum_{\epsilon} x_{\epsilon,t} \le 1 \ \forall t \quad \forall \epsilon \in E\setminus F$