1

When dealing with a mortgage company, paying off a loan is quite simple. Now everything is online and most of the times you can pay more than the minimum payment each time. Each month the interest then changes to adapt to the new balance that is less than the assumed balance had you paid the minimum each recurring month. If you are dealing with a private loan, and want to make extra payments when cash is available, what is the best way to calculate interest and balance left after each payment?

Is the best option to just calculate the interest rate each day after a payment to know the next occurring interest charge + current balance due?

I was looking online and have only found amortization charts that would become invalid the first time I make a payment over the minimum amount.

CCCBuilder
  • 111
  • 2
  • 1
    The google search "mortgage loan amortization excel" should return to you various templates which have an "extra payments" column. (I used such a spreadsheet for my private mortgage.) – RonJohn Jan 26 '18 at 14:50
  • @RonJohn - I have looked and the ones I find with extra payment are actually just an assumed constant extra payment...not a random $50 or $150 mid-term for example or not always with the monthly payment. – CCCBuilder Jan 26 '18 at 15:50
  • There's a link at the bottom of http://www.tvmcalcs.com/calculators/apps/excel_loan_amortization_with_extra_payments with a spreadsheet that allows extra payments. It defaults to a constant extra payment, but you can zero out that cell and add individual amounts to cells in column E. – RonJohn Jan 26 '18 at 15:57

2 Answers2

0

The exact calculation will depend on how the method of interest calculation. The common practice in the United States is to apply a monthly interest that is 1/12 of the stated annual rate. This monthly rate is charged against the principal balance for the month.

Assuming the above.

  1. Let p0 be the principal balance after payments applied last month.
  2. Let i1 be the interest to be paid this month. i1 = p * (stated interested rate)/ 12.
  3. p1 = p0 - (payment - (i1 + escrow + fees)) - (extra payment)
  4. Set p0 to p1, repeat next month until p1 is zero.

For a spreadsheet, use a line for each month, looking to the previous line to get p0, and then you have a running balance.

Shannon Severance
  • 902
  • 6
  • 9
-1

If you are increasing the repayment amount once part way through the loan term the calculations for total interest and term reduction are laid out here:

Extra Repayment loan calculator

Repeated changes to the repayment amount might be more simply calculated on a spreadsheet.

Further to downvote

I will leave this answer here for a while in case I get round to calculating a formula for multiple repayment amount changes. Otherwise the question will probably be closed. This happened before, while I was calculating. As it is this question already has 4 close votes. No idea why.

Example

Considering a loan where the payments are increased each year: 

d1 = 2000
d2 = 2500
d3 = 3000
d4 = 3295.86

The principal is £100,000 and the interest rate is 1% per month.

s = 100000
r = 0.01

The payments are increased after 12, 24 and 36 months. When will the loan be paid down?

m = 12
n = 24
o = 36
p = ?

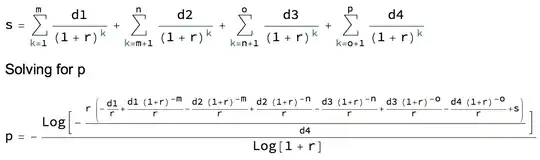
enter image description here

p = -(Log[-((r (-(d1/r) + (d1 (1 + r)^-m)/r - (d2 (1 + r)^-m)/r +
     (d2 (1 + r)^-n)/r - (d3 (1 + r)^-n)/r + (d3 (1 + r)^-o)/r -
     (d4 (1 + r)^-o)/r + s))/d4)]/Log[1 + r]) = 48 months

Now increase two of the payments

d2 = 2900
d3 = 3248

p = 45 months

The term of the loan is shortened by 3 months.

Comparing the formulae for loan terms with 3, 4 & 5 repayment changes, extending to o, p & q months, one can see how the general formula for any number of changes could be constructed.

enter image description here

Of course, if you have a computer algebra program like Mathematica you can leave the calculation in the form of a summation, which makes the calculation as easy as it could be. Just add a new summation for each repayment change.

m = 12
n = 24
o = 36

s = 100000
r = 0.01
d1 = 2000
d2 = 2900
d3 = 3248
d4 = 3295.86

enter image description here

Chris Degnen
  • 9,797
  • 1
  • 20
  • 36