I have to calculate a split loan calculator.As I know that,Split means combo we are get benefits of both interest type.I have calculated a many things are right but problem with Total Payable interest.
Update what is Total payable interest ? How would I calculate in case for split loan?
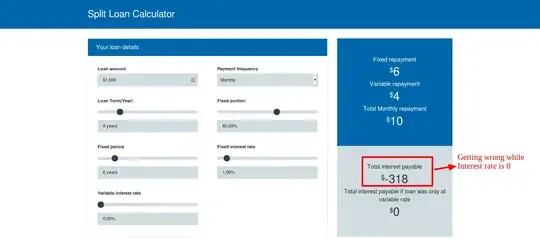
The total interest payable in the OP's screenshot: $56, does not match the result calculated below, $28. However, the other figures do match up. The $56 result could be due to an error on the web form. Maybe try again in a refreshed webpage.
The calculation is laid out below.
Source: Mortgage Choice - Split loan repayments calculator
Starting the calculation using the standard repayment formula.
s is the principal
rf & rv are the fixed and variable rates
pf is the percentage of the loan that is fixed
sf & sv are the fixed and variable portions of the loan
n is the full term of the loan
df & dv are the fixed and variable repayment during the fixed period
s = 1000
rf = 0.01/12
pf = 0.6
sf = s*pf = 600
n = 2*12 = 24
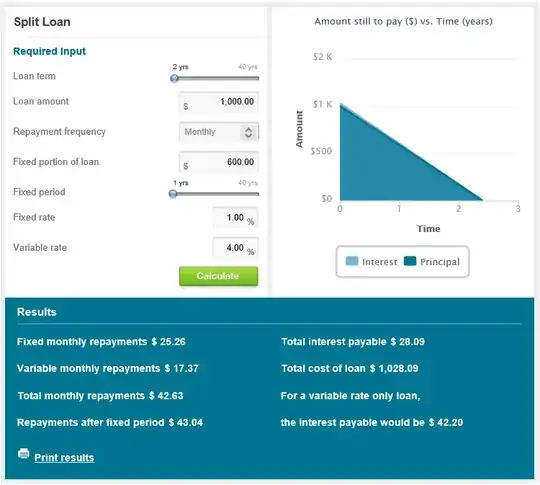
df = (rf (1 + rf)^n sf)/((1 + rf)^n - 1) = 25.2612
rv = 0.04/12
sv = s (1 - pf)
dv = (rv (1 + rv)^n sv)/((1 + rv)^n - 1) = 17.37
The calculation of the fixed and variable repayments (for the fixed period) confirms the method for the initial values being used by the online calculators.
The next step uses a recurrence formula to calculate the balance at the end of the fixed period. Based on the following expression for the month-to-month loan remaining m, a recurrence formula has been calculated.
m[nf + 1] = m[nf] pf (1 + rf) - df + m[nf] (1 - pf) (1 + rv) - dv
where m[0] = s
With the number of fixed periods nf = 12 the recurrence formula below gives the total loan remaining at the end of month 12:
m[nf] = m[12] =
(df + dv - (1 + pf (rf - rv) + rv)^nf (df + dv - (pf rf + rv - pf rv) s))/
(pf (rf - rv) + rv) = 505.459
Next, the standard loan formula is used to calculate the repayment d for the variable-only portion of the loan.
nv = n - nf = 12
d = (m[nf] rv (1 + rv)^nv)/((1 + rv)^nv - 1) = 43.0397
Calculating the interest
total interest = (df + dv) nf + d nv - s = 28.0516
Running a check with different figures
Source: ING Home Loans Calculator
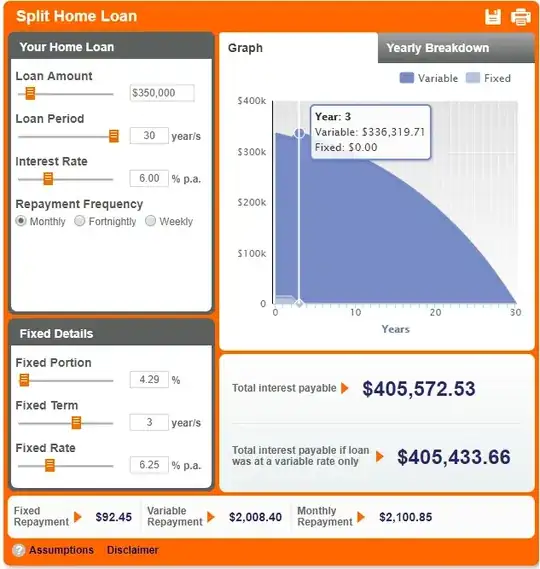
Note: further to the OP's question in comments the version below includes alternative calculations for the case where the variable rate of interest is zero.
s = 350000
rf = 0.0625/12
pf = 4.29/100
sf = s*pf
n = 30*12
df = (rf (1 + rf)^n sf)/((1 + rf)^n - 1) = 92.4499
rv = 0.06/12
sv = s (1 - pf)
dv = If[rv == 0,
sv/n,
(rv (1 + rv)^n sv)/((1 + rv)^n - 1)] = 2008.4
df + dv = 2100.85
nf = 3*12 = 36
m = If[rv == 0,
(df + dv - (1 + pf rf)^nf (df + dv - pf rf s))/(pf rf),
(df + dv - (1 + pf (rf - rv) + rv)^nf (df + dv - (pf rf + rv - pf rv) s))/
(pf (rf - rv) + rv)] = 336319.61
nv = n - nf = 324
d = If[rv == 0,
m/nv,
(m rv (1 + rv)^nv)/((1 + rv)^nv - 1)] = 2098.59
totalinterest = (df + dv) nf + d nv - s = 405572.34
Checks out within acceptable calculation precision variation.
