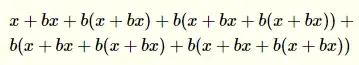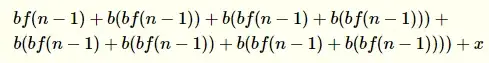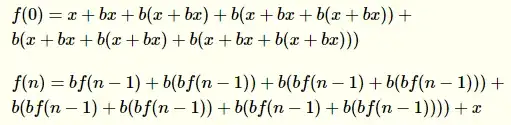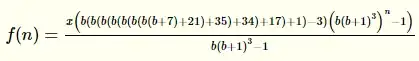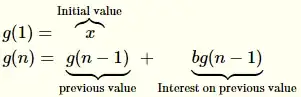2

I have searched and not seen (or maybe just didn't recognize it as applying to) a future value formula for the following: Deposit a fixed amount ($100 or whatever) each month into an account/investment. Compound interest is applied weekly (or it could be daily, bi weekly, but less than monthly). Annual interest rate (would be divided by the number of compounding periods per year, I assume). No initial investment (so account/investment would start with $0). Deposit would be at the end of each month.

I've seen a formula (in various places) that is close (or possibly THE formula for this) but can't seem to get it to work with the deposits being monthly and the compounding periods being less than monthly.

If there is a formula somewhere, or if this question has already been answered, could someone please point me to it? I apologize ahead of time if this is the case.

Long John Dough
  • 23
  • 3

2 Answers2

2

There is no formula that can be applied to most variations of the problem you pose. The reason is that there is no simple, fixed relationship between the two time periods involved: the time interval for successive payments, and the time period for successive interest compounding.

Suppose you have daily compounding and you want to make weekly payments (A case that can be handled). Say the quoted rate is 4.2% per year, compounded daily

Then the rate per day is 4.2/365, or 0.0115068 %

So, in one week, a debt would grow through seven compoundings. A debt of $1 would grow to 1 * (1+.000225068)^7, or 1.000805754

So, the equivalent interest rate for weekly compounding is 0.0805754%

Now you have weekly compounding, and weekly payments, so the standard annuity formulas apply.

The problem lies in that number "7", the number of days in a week. But if you were trying to handle daily / monthly, or weekly / quarterly, what value would you use?

In such cases, the most practical method is to convert any compounding rate to a daily compounding rate, and use a spreadsheet to handle the irregularly spaced payments.

DJohnM
  • 4,294
  • 2
  • 15
  • 19
  • I had a strong suspicion that there might not be a formula (hence the fact none I found on the internet seemed to fit the bill) as I was having trouble trying to see if the two different time periods could be made to work together, and failing. Thanks for pointing that out! I'll certainly try out converting to a daily rate. That does appear to be the only way that makes sense. – Long John Dough Aug 09 '16 at 16:28
-3

Perhaps there is no single formula that accounts for all the time intervals, but there is a method to get formulas for each compound interest period. You deposit money monthly but there is interest applied weekly. Let's assume the month has 4 weeks.

So you added x in the end of the first month, when the new month starts, you have x money in your account. After one week, you have x + bx money. After the second week, you have x + b(x + bx) and so on. Always taking the previous ammount of money and multiplying it by the interest (b) you have. This gives you for the end of the second month:

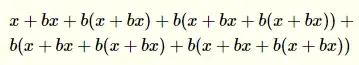
enter image description here

This looks complicated, but it's easy for computers. Call it f(0), that is: It is a function that gives you the ammount of money you would obtain by the end of the second month. Do you see that the future money inputs are given with relation to the previous ones? Then we can do the following, for n>1 (notice the x is the end of the formula, it's the deposit of money in the end of the month, I'm assuming it'll pass through the compound interest only in the first week of the next month):

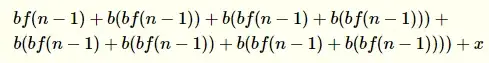
enter image description here

And then write:

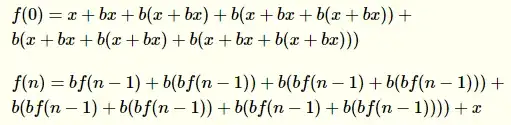
enter image description here

There is something in mathematics called recurrence relation in which we can use these two formulas to produce a simplified one for arbitrary b and n. Doing it by hand would be a bit complicated, but fortunately CASes are able to do it easily. I used Wolfram Mathematica commands:

FullSimplify[
 RSolve[{f[0] == 
    x + b x + b (x + b x ) + b (x + b x + b (x + b x )) + 
     b (x + b x + b (x + b x ) + b (x + b x + b (x + b x ))),
   f[n] == b f[n - 1] + b (b f[n - 1]) + 
     b ( b f[n - 1] + b (b f[n - 1])) + 
     b (b f[n - 1] + b (b f[n - 1]) + 
        b ( b f[n - 1] + b (b f[n - 1]))) + x}, f[n], n]
 ]

And it gave me the following formula:

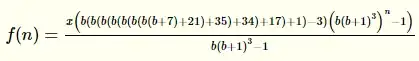
enter image description here

All the work you actually have to do is to figure out what will be f(0) and then write the f(n) for n>0 in terms of f(n-1). Notice that I used the command FullSimplify in my code, Mathematica comes with algorithms for simplyfing formulas so if it didn't find something simpler, you probably won't find it by yourself! If the code looks ugly, it's because of Mathematica clipboard formatting, in the software, it looks like this:

enter image description here

Notice that I wrote the entire formula for f(0), but as it's also a recurrence relation, it can be written as:

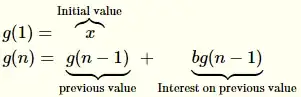
enter image description here

That is: f(0)=g(4). This should give you much simpler formulas to apply in this method.

Community
  • 1
Red Banana
  • 95
  • 4
  • 2
    Alas, this is not quite correct because a month is not the same as four weeks, as DJohnM points out (except for February in non-leap years). According to your formula, weekly interest would be paid only 48 times in a year. – Dilip Sarwate Aug 01 '16 at 12:16
  • @DilipSarwate Exercise: Figure out why what you said is a completely wrong. (Hint: In mathematics, it's customary to use the symbol ∀ which means "for all". With this, we can say that...) – Red Banana Aug 01 '16 at 14:54
  • @Voyska: You said right at the beginning of your answer that you assume the month has four weeks. – BrenBarn Aug 01 '16 at 17:41
  • 1
    What nonsense! -1 for writing it instead of fixing your answer – Dilip Sarwate Aug 01 '16 at 17:45
  • @BrenBarn I could assume that the month had n weeks. So instead of writing using g(4), I'd use g(n). – Red Banana Aug 01 '16 at 17:55
  • That's the part @DilipSarwate didn't understand, which is a shame: The guy was a professor of electrical and computing engineering - The idea that that example could be adapted to any situation with a little adaptation should be natural to him (I've even tried to give him a hint, but he got emotional and instead of trying to understand, he downvoted me). He even has some quite interesting questions in mathematics.se. How he was unable to figure it our is completely unclear to me. – Red Banana Aug 01 '16 at 18:01
  • The point is: The nature of compound interest is mainly made with recurrence relations. What I gave was a simple example of how one could think about such things. Too bad that when I write an example with 4 as an example, you guys are able to understand only that it deals with the 4 case instead of abstracting it and understanding that it would work for any n. – Red Banana Aug 01 '16 at 18:05
  • @Voyska: But a month does not have n weeks. What do you do if the ratio of months to weeks is not an integer (as indeed it is not)? – BrenBarn Aug 01 '16 at 19:41
  • @BrenBarn 1: I didn't said the relation is an integer. 2: You put some money on one month. Now it will yield interest in the end of the first week (as an example). How many ends of week does a month have? Is it an integer? Is it a irrational number? Is it a complex number? Any end of week that ends up in the next month is an end of week in the next month, so the number is an integer. In my whole example, the ratio of weeks to months is irrelevant. (I'm unable to think how you thought that the ratio would be relevant). – Red Banana Aug 01 '16 at 20:10
  • 1
    @Voyska Now that your Trump imitation is over and done with, consider the case when monthly deposits are made on the first of the month, and the weekly interest is credited on Mondays and is for the balance in the account from the previous Monday till the end of day before (Sunday). Specifically, suppose that the first deposit was made on Monday August 1, 2016, and no interest was credited that day because the previous week's balance was 0. So, interest will be paid on 8/8, 8/15, 8/22, and 8/29 exactly as you have described. But, what happens the following week? (continued...) – Dilip Sarwate Aug 03 '16 at 21:39
  • 1
    (continuation...) On Thursday September 1, the second deposit occurs, and increases the amount on deposit in the middle of the week. So, is the interest paid on Monday September 5 the interest on the beginning balance as of 8/29 (as per your formulas) or the ending balance as of 9/4 (which would be very generous) or the average balance from 8/29 to 9/4 (which most people would expect)? So, after you fix your formulas to account for this, remember that the monthly deposit will occur on Saturday 10/1 and the next interest crediting will be on Monday 10/3 (continued...) – Dilip Sarwate Aug 03 '16 at 21:50
  • 1
    (more continuation...) so your newly developed changed formula will need modification one more time and so it will go on. If the whole process began on a different date, you would need to re-rewrite all your formulas all over again. Read the first two sentences of DJohnM's and them to heart. I will take the liberty of suggesting to you that you should give serious thought to deleting all the snarky comments that you have directed towards me and BrenBarn, or even better, delete your entire Answer because it is not fixable. But if you want to write yet another Trumpian response... – Dilip Sarwate Aug 03 '16 at 22:00
  • @DilipSarwate Yes, what you wrote is obvious. What you didn't take into account is that he could easily adapt it to obtain an approximation (I even show it how it could be done). I suggest you to read the following by heart: The point is: The nature of compound interest is mainly made with recurrence relations. What I gave was a simple example of how one could think about such things. - But I am happy that you decided to at least put some effort and find a more decent problem than telling me that "some months do not have 4 weeks"! – Red Banana Aug 04 '16 at 05:10
  • @DilipSarwate Also, what you understand as formula is quite problematic. I gave more than one formula. The programming code is also a formula. With a simple modification, you could adapt it to all the situations you mentioned. In the end, there is a unique formula (the programming code which generate all sorts of formulas and that you are unable to see as a formula). I guess you guys are still struggling to understand that I gave an example and that adapting the code could actually yield a master formula which yields all the desired formulas. – Red Banana Aug 04 '16 at 05:17
  • @DilipSarwate You should really meditate on what is the meaning of formula. What you point as a formula is not actually the main formula I gave... If it helps, here's a starter. – Red Banana Aug 04 '16 at 05:19
  • @DilipSarwate And please, you do not need to tell me more obvious things (it's becoming annoying already...). I knew everything you said when I was typing my answer. I won't erase my answer nor my comments (that's how I differ from Trump perhaps?). If needed, ask your friends to join SE and downvote my answers? I promise I'll be scared under my bed. If any other point is made by you, I promise you can address it by just thinking. It's a wonderful trick with lots of applications! You should try it yourself! – Red Banana Aug 04 '16 at 06:04
  • More snark, and just like Trump, doubling down on something that is incorrect and refusing to withdraw or fix your answer. – Dilip Sarwate Aug 04 '16 at 13:08
  • @Voyska - Thanks for your time. I will have spend a bit of time with this myself, to really get my head around it. I'd never even heard of computer algebra systems before. Pretty cool. – Long John Dough Aug 09 '16 at 16:45
  • @LongJohnDough You're welcome! Using the answer I provided, you can easily obtain an approximation to what you're looking for. But for an exact measure, things will get a little more complicated as pointed by others. – Red Banana Aug 09 '16 at 18:06