Building on my previous answer here
r is the monthly or quarterly interest rate
y is the number of years
m is the number of months or quarters per year
p is the initial regular deposit
x is the annual deposit percentage increase
c is the initial capital
fv = (p (1 + r) (-1 + (1 + r)^m) ((1 + r)^(m y) - (1 + x)^y))/
(r (-1 + (1 + r)^m - x)) + c (1 + r)^(m y)
For 5% compounded annually the monthly rate r = (1 + 0.05)^(1/12) - 1
For 5% compounded monthly the monthly rate r = 0.05/12
See nominal rate calculation for clarification.
With the following values (compounded monthly rate)
r = 0.05/12
m = 12
p = 1000
x = 0.03
c = 2000
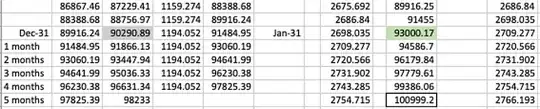
fv = 100000
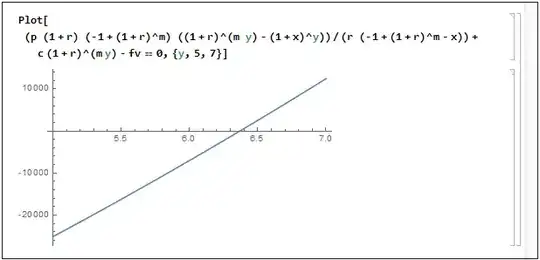
Solving for y : y = 6.36822
The target is reached in 6 years and 5 months.
Also showing the solution plotted.
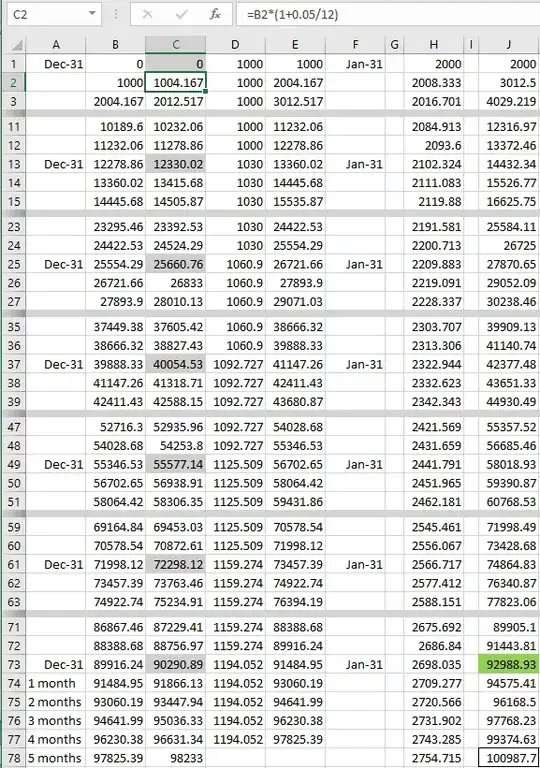
Checking result for y = 6 using formula and Excel.
fv = (p (1 + r) (-1 + (1 + r)^m) ((1 + r)^(m y) - (1 + x)^y))/
(r (-1 + (1 + r)^m - x)) + c (1 + r)^(m y) = 92988.93
The compounded capital is listed separately in column H, i.e. c (1 + r)^(m y)
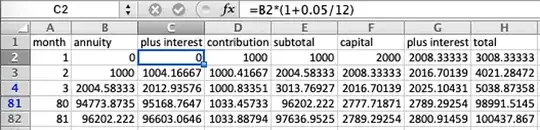
Note, probably due to the annual jumps in the monthly contribution only round year inputs exactly match the Excel figures, i.e for y = 6 + 5/12
fv = (p (1 + r) (-1 + (1 + r)^m) ((1 + r)^(m y) - (1 + x)^y))/
(r (-1 + (1 + r)^m - x)) + c (1 + r)^(m y) = 100936.25
Also the first month's interest on the capital was missed. Excel cell J1 above should be 2008.333 and the formula should end ... + c (1 + r)^(m y + 1). The capital interest is correct in the version below.
Additional question
Switching to monthly contribution increase of 0.5 %
fv = (p ((1 + r)^n - (1 + x)^n))/(r - x) + c (1 + r)^n
where x is the monthly contribution percentage increase and n is the number of months.
The formula again cannot be expressed for n.
I will see about following up with Newton's method for solving this fast, computationally (without a 3rd party solver).

Newton-Raphson solution for n
We need to find a root for this formula with one unknown, n
(p ((1 + r)^n - (1 + x)^n))/(r - x) + c (1 + r)^n - fv = 0
Using the algorithm here: https://en.wikipedia.org/wiki/Newton%27s_method#Code
This method requires the derivative of the formula. (The formula and its derivative will work for all the numerical variations of the calculation. Note Log is to base e.)

Quite what n = 80.6977 means in this context is questionable. For sure you can know that the penultimate payment is the 80th.
r = 0.05/12; p = 1000; x = 0.005/12; c = 2000; n = 80;
fv = (p ((1 + r)^n - (1 + x)^n))/(r - x) + c (1 + r)^n = 98991.5145
By the end of month 80 fv = 98991.5145 (1 + r) = 99403.9792
and then the last contribution comes in and takes the balance over the target 100000. So what happens at n = 80.6977 is a bit theoretical.
You could more easily find the penultimate month with a simple loop.
r = 0.05/12; p = 1000; x = 0.005/12; c = 2000; fv = 100000; n = 0;
While[c < fv,
u = {n++, c};
c *= (1 + r);
c += p;
p *= (1 + x)]
{u, {n, c}}
{{80, 98991.5145}, {81, 100438.867}}
Addendum
Adding a Newton-Raphson solution for the (corrected) annually increasing payment annuity.

The solution tells you the goal is reached in year 6. So adding a loop to find the penultimate and final month.
y = 6
fv = (p (1 + r) (-1 + (1 + r)^m) ((1 + r)^(m y) - (1 + x)^y))/
(r (-1 + (1 + r)^m - x)) + c (1 + r)^(m y + 1) = 93000.17
n = 0;
While[fv < 100000,
u = {n++, fv};
fv = (fv + p (1 + x)^y) (1 + r)]
{u, {n, fv}}
{{4, 99386.06}, {5, 100999.2}}
In this case the goal is reached before the monthly payment is made. The case where the goal is reached or exceeded after the payment would also have to be handled.