As a follow-up to this question, what is the minimum size of a nest egg to support 30 years of $5,583.33 monthly distributions? I want the $5,583.33 to increase with inflation each month.
The present value of the first payment should be $5,583.33.
First withdrawal will be in 20 years: $5,583.33*(1 + 0.0033)^240 = $12,310.86
Here is what I've pieced together from this question:
Total withdrawals: n = (30 years)(12 months) = 360 payments
Inflation per period: i = 4.0% per year / 12 = 0.3333% per period)
Return per period: m = 8.0% per year / 12 = 0.6666% per period)
Periods until 1st payment: o = (20 years)(12 months) = 240 periods
First payment amount: w = $67,000 / 12 = $5,583.33 (today's dollars)
p = ([(1 + i)^o]*[(1 + m)^-n]*((1 + i)^n - (1 + m)^n)*w)/(i - m)
p = ([(1 + 0.0033)^240]*[(1 + 0.00667)^-360]*((1 + 0.0033)^360 - (1 + 0.00667)^360)*5583.33)/(0.00333 - 0.00667)
p = $2,594,790.06
where
n is the number of payments to be received
o is the number of the period at the end of which the first payment is received
w is the payment amount
m is the pension fund's periodic rate of return
i is the periodic inflation rate
Is this the right equation? From what I could find on Google, this calculation is called the present value of a growing or graduated annuity. Is this correct?
Is it correct to say that $2.5 million is the nest egg balance 20 years from now on the day the first withdrawal is made? And that $2.5 million is not in today's dollars but in equivalent dollars 20 years from now?

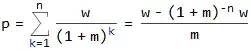
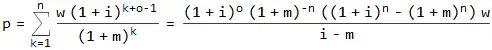
oset to 240 you are applying 240 months of inflation to the first payment, so it will not be $5,583.33 but5583.33*(1 + 0.0033)^240 = 12310.86. The present value of the first payment is $5,583.33 but the actual first payment will be $12,310.86. Likewise, the actual value of the pot at the end of the saving period will be $2.5 million but its present value is $1.2 million. I.e. $1.2 will buy the same quantity of goods now as $2.5 will buy in twenty years' time. – Chris Degnen Oct 26 '18 at 11:3860k*1.02^20 = 89k/year. – Chris Degnen Oct 26 '18 at 12:3589k/0.04 = 2,225,000is not far off the $2,307,538 calculated here, which has the fund rate of return at 3% and increases pension payouts in line with inflation. – Chris Degnen Oct 26 '18 at 13:18