How to picture $\mathbb{C}_p$?

Question

I hope this is appropriate for mathoverflow. Understanding $\mathbb{C}_p$ has always been something of a stumbling block for me. A standard thing to do in number theory is to take the completion $\mathbb{Q}_p$ of the rationals with respect to a $p$-adic absolute value. The resulting field is then complete, but has no good reason to be algebraically closed. You can take its algebraic closure, but that is not complete, so then you take the completion of that, and get a field which is both complete, and algebraically closed, denoted by $\mathbb{C}_p$.

I understand that it is a reasonable desire to have a field extension of $\mathbb{Q}_p$ that is both complete and algebraically closed; my trouble, however, is getting some sort of grasp on how to picture this object, and to develop any intuition about how it is used. Here are my questions; I'd imagine the answers are related:

1. Am I even supposed to be able to picture it?
2. Is there some way I ought to think of a typical element?
3. Is it worth it, in terms of these goals, to look at the proofs of the assertions in my first paragraph?
4. How is $\mathbb{C}_p$ typically used? (this question may be too vague, feel free to ignore it!)

Please feel free to answer any or all of these questions.

Answer 1

I'll suggest a way to get a hold on $\mathbb{C}_p$ in a "pictorial" way. It is supposed to be similar to viewing $\mathbb{C}$ as a plane acting on itself via rotations, scalings, and translations.

There's a usual picture of $\mathbb{Z}_p$, which looks like the thing below for $p=3$ (taken from the website of Heiko Knospe):

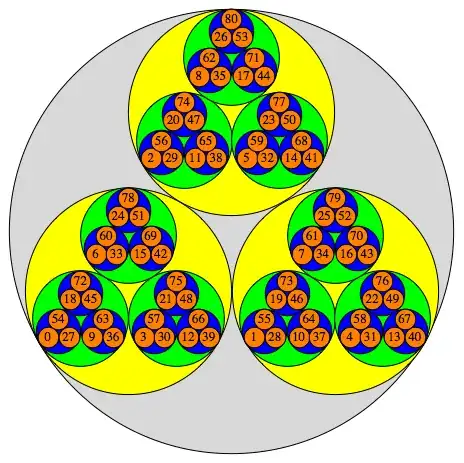
Here the outermost circle is all of $\mathbb{Z}_3$; the three large colored circles are the residue classes mod $3$, the smaller circles are the residue classes mod $9$, and so on. If you want to think about $\mathbb{Q}_p$, imagine this picture continued infinitely "upward," (e.g. this circle is accompanied by two others, inside some larger circle, accompanied by two others, etc.).

Now the operations of multiplication and addition do something very geometric. Namely, addition cyclically permutes the residue classes (of each size!) by some amount, depending on the coefficient of $p^n$ in the $p$-adic expansion of whatever $p$-adic integer you have in mind. Multiplication by a unit switches the residue classes around as you'd expect, and multiplication by a multiple of $p^n$ shrinks the whole circle down and sends it to some (possibly rotated) copy of itself inside the small circle corresponding to the ideal $(p^n)$.

Now zero has the $p$-adic expansion $0+0\cdot p+0\cdot p^2+\cdots$ and so it is the unique element in the intersection of the circles corresponding to the residue class $0$ mod $p^n$ for every $n$. So we have a way to think of zeroes of polynomials over $\mathbb{Q}_p$---namely, a Galois extension of $\mathbb{Q}_p$ is some high dimensional vector space $\mathbb{Q}_p^N$ (which you probably have a picture of from linear algebra) acted on by $\mathbb{Q}_p$, in a way that twists each factor of $\mathbb{Q}_p^N$ and permutes the factors of the direct sum, according to the Galois action. That the extension is algebraic means that there's some way to twist it about (using the previously described actions) to put any element at the $0$ point.

Totally ramified extensions add intermediate levels of circles between those that already exist, whereas unramified extensions add new circles. I think this point of view is a particularly appealing visualization.

Now, the algebraic closure of $\mathbb{Q}_p$ is some maximal element of the poset of these algebraic extensions---which is hard to visualize as it is not really "unique," but for the sake of a picture one might think of choosing embeddings $K\to K'$ for each $K'/K$, and then taking the union. Finally, think of the completion in the usual way, e.g. by formally adding limits of Cauchy sequences.

Trying to draw pictures of some finite algebraic extensions of $\mathbb{Q}_p$ might help, and figuring out what the actions by addition and multiplication are is a fun exercise. I hope this "word picture" is as useful for you as it is for me.

---

ADDED: Though this answer is becoming rather long, I wanted to add another picture to expand on the points I made about unramified and totally ramified extensions above.

Here is a picture of $\mathbb{Z}_3$, which I made with the free software Blender; imagine it continuing indefinitely upward:

A top view of this object should be the previous picture; the actual elements of $\mathbb{Z}_3$ should be viewed as sitting "infinitely high up" on the branches of this tree. As you can see, this object splits into levels, indexed by $\mathbb{N}$, and on the $n$-th level there are $p^n$ "platforms" corresponding to the residues mod $p^n$. For $\mathbb{Q}_p$, the levels should be indexed by $\mathbb{Z}$.

Now what happens when one looks at an unramfied extension of degree $k$? The levels, which correspond to powers of the maximal ideal, should not change, so the levels are still indexed by $\mathbb{Z}$; but the amount of branching on each "platform" is now indexed by $\mathcal{O}_K/m=\mathbb{F}_{p^k}$. So instead of having $p$ branches coming out of each level, one has $p^k$.

On the other hand, what if we have a totally ramified extension of degree $k$? Now $\mathcal{O}_k/m=\mathbb{F}_p$, so there are still $p$ branches on each level. But because the uniformizer now has valuation $1/k$, we can view the levels as being indexed by $\mathbb{Z}[1/k]$ (if you like, the height of each platform is now $1/k$ rather than $1$).

So what is the upshot for $\mathbb{C}_p$? We can view it as a similar diagram, except the levels are indexed by $\mathbb{Q}$, and the branches coming off of an individual platform correspond to elements of $\overline{\mathbb{F}_p}$.

One nice thing about this picture is that one can actually build spaces like the one I've included in the picture---replacing the tubes in my picture with line segments---such that the elements of $\mathbb{Q}_p$ or some extension thereof are a subset of the space (living "infinitely far" from the part I've drawn), with the subspace topology being the usual topology on the local field. Furthermore, the construction is functorial, in that an embedding $K\hookrightarrow K'$ induces a continuous map of spaces. The distance between two points in the local field is then given by their "highest common ancestor" in this garden of forking paths.

(This picture is essentially a description the Berkovich spaces mentioned by Joe Silverman, though I am essentially a novice in that regard, so it's quite possible I've made some mistake; you should take this as a description of my intuition, not Berkovich's definition.)

Answer 2

Among the reasons that $\mathbf{C}_p$ is hard to "visualize" are the it is totally disconnected (as is $\mathbf{Q}_p$) and it is not locally compact. The lack of local compactness means, for example, that you can't put a nice measure on $\mathbf{C}_p$. Many people these days instead work on the Berkovich affine line $\mathbf{A}_p^{Berk}$ or the associated Berkovich projective line $\mathbf{P}_p^{Berk}$. The Berkovich line is a topological space that

1. contains a copy of $\mathbf{C}_p$ as a topological space
2. is (simply) connected;
3. is locally compact.

So people do measure theory, and even harmonic analysis, on Berkovich spaces. You can find a brief introduction, with some pictures, in my book The Arithmetic of Dynamical Systems, Springer, Section 5.10. For a more complete introduction, there's a great new book by Baker and Rumely, Potential Theory and Dynamics on the Berkovich Projective Line, American Mathematical Society, 2010.

Final comment: The fact that $\mathbf{C}_p$ is not spherically complete, which was mentioned by Pete L. Clark, plays a role in Berkovich space. More precisely, it leads to some extra points that are needed to make Berkovich space complete.

Answer 3

1. You do whatever works for you. Some people think more algebraically, others more geometrically. I certainly don't know what "to picture" means in this context, but then, I am a more algebraic person, so maybe others will be able to say more. Can you picture $\mathbb{Q}^{ab}$, say? I can't.

2. A typical element is, by definition, represented by a Cauchy sequence of elements of $\overline{\mathbb{Q}}_p$. Each of the elements in the Cauchy sequence lives in a finite extension of $\mathbb{Q}_p$, so you can view it in the usual way, as a power series in a uniformiser of that finite extension with coefficients in a finite field. But the field $\overline{\mathbb{Q}}_p$ itself is not discretely valued, so you cannot pick a common uniformiser for all the numbers in your Cauchy sequence.

3. Yes! In my opinion, that's the only way to get a feel for all the fields involved.

4. That one really is too broad. As you may guess, these fields always come in when you need something $p$-adic that is complete and algebraically closed at the same time. Sometimes, you only need something that is complete and has an algebraically closed residue field. Then, people work with the completion of $\mathbb{Q}_p^{nr}$. For example, these fields are used all the time in $p$-adic Hodge theory (you will find many introductions if you google) and, consequently, in the theory of Galois representations. To expand on that would require a whole essay, which I'm afraid I am not qualified to write.

Answer 4

Since there are already several very good answers, I just discuss question 4 (how is ${\mathbb C}_p$ typically used?) with one example of use which made a great impression on me when I learnt it, and made me think that ${\mathbb C}_p$ was something deep and serious, and not only a very amusing curiosity. This example is a theorem of Tate and Sen, which states that if $V$ is a finite-dimensional over $\mathbb{ Q_p}$ vector space with a continuous linear action of $G=$Gal$(\overline{\mathbb Q_p}/{\mathbb Q_p})$ (that is, $V$ is a $p$-adic representation of $G$), then the following are equivalent:

(1) $\dim_{\mathbb Q_p} (V \otimes {\mathbb C_p})^{G} = \dim_{\mathbb Q_p} V.$ (Here, G acts on $\mathbb{C_p}$ by extending by continuity its action on $\overline{\mathbb Q_p}$ and it acts on $V \otimes {\mathbb C_p}$ by acting on both factors.)

(2) The inertia subgroup of $G$ acts on $V$ through a finite quotient (in more knowledeable words, $V$ is potentially unramified).

To appreciate this theorem, it may be useful to solve for oneself the following elementary exercise: if in (1), ${\mathbb C}_p$ is replaced by $\overline {\mathbb Q_p}$, then (2) should be replaced by "$G$ acts on $V$ through a finite quotient". Somehow, replacing $\overline {\mathbb Q_p}$ by its completion allows (1) to see inside the group $G$ and detect the behaviour of the inertia subgroup in it.

I believe that someone who understands the proof of this theorem has necessarily a good understanding of $\mathbb{C}_p$, and this will be my answer to question 3 as well: knowing the proof of the basic assertions on $\mathbb{C}_p$ given in the questions is a first step into a good understanding of that field and its elements, but won't take you very far. Learning the proof of the above theorem will let you get a much deeper look inside $\mathbb{C}_p$ -- and in addition you will learn a nice result, which is a first step in the fundamental $p$-adic Hodge Theory.

Answer 5

1. No, not necessarily. It is hard to get a faithful geometric picture of a non-Archimedean space. It may be helpful to have schematic approximate pictures in mind like in Daniel Litt's answer, but it is just as important to recognize the limitations of these pictures. Speaking only for myself, contemplating the picture in Daniel's answer did not help me understand $p$-adic numbers: I was exposed to the picture offhandedly in a course I took as a college freshman, but it didn't make much sense to me until I studied the algebraic and metric properties of non-Archimedean fields more carefully (at a later time). Pictures here are a form of intuition. Having intuition is always helpful and at times indispensable, but importing others' intuition often does not work: you need to develop your own.

2. I would say no to this as well. Of course you should understand what $\mathbb{C}_p$ means and how it is constructed, but in general thinking of algebraic structures element by element is not so useful. By this I mean that rather than thinking of an element of $\mathbb{C}_p$ as a certain Cauchy sequence of elements in algebraic extensions of $\mathbb{Q}_p$ of varying degree, it is just as useful, and logically simpler, just to think of $\mathbb{C}_p$ as a complete, normed field containing a dense copy of the algebraic closure of $\mathbb{Q}_p$ with the (unique) extension of the $p$-adic metric.

3. Oh, yes. You should definitely understand why the completion of the algebraic closure of the $p$-adic completion of $\mathbb{Q}$ is algebraically closed! Of course, it's best if you can embed this fact into a general understanding of non-Archimedean fields rather than learning and memorizing an argument which shows exactly this. For instance, in these notes I deduce (Corollary 22) the fact that the completion of a separably closed normed field is separably closed from Krasner's Lemma, which to me personally has become one of the most useful and meaningful parts of the entire theory. Later on I show that a complete, separably closed field is necessarily algebraically closed (Proposition 27). These are the right explanations for me, and I think they are good ones, but I'm not saying they need to be the right explanations for you. Maybe something else speaks to you more than Krasner's Lemma.

4. Why are you lamenting your lack of understanding of $\mathbb{C}_p$ if you don't know how it is used? (This is not meant to be rhetorical or combative: it's a sincere question.) There are a lot of different answers in different areas of mathematics. Moreover, for many people (and even some number theorists), the honest answer is that it is not used for anything in particular. For instance, above I referred to some of my notes for a course I taught last spring on local fields and adeles. From the perspective of those notes, the Henselian field $\overline{\mathbb{Q}_p}$ is just as good and perhaps more natural. On the other hand, for some people going to $\mathbb{C}_p$ is not far enough: it is not spherically complete, meaning that the key property of a locally compact field like $\mathbb{C}$ or $\mathbb{Q}_p$ that a nested sequence of closed balls necessarily has nonempty intersection does not hold in general. If you want to do serious $p$-adic functional analysis -- e.g. if you want things like the Hahn-Banach Theorem to hold -- then you want to work in $\Omega_p$, the spherical completion of $\mathbb{C}_p$. But my guess is that the average working number theorist doesn't even know what $\Omega_p$ is, so it depends a lot on what you want to do.

(Edit: the link to the notes is broken, but see here instead. Krasner's Lemma appears on page 78 of the pdf.)

Answer 6

One point that I don't think anyone has mentioned yet is that $\mathbb{C}_p$ is isomorphic (as an untopologised field) to $\mathbb{C}$. More generally, any two uncountable algebraically closed fields of the same characteristic and cardinality are isomorphic, if I remember correctly. Of course the proof is horrendously non-constructive, but the very definition of $\mathbb{C}_p$ is already horrendously non-constructive. So instead of worrying about what $\mathbb{C}_p$ is, you can instead worry about why $\mathbb{C}$ admits a $p$-adic metric with respect to which it is complete. I don't have anything to offer about that.

[Corrected as per Johannes Hahn's comment]

Answer 7

You may, or may not, be able to derive some inspiration from "Artist's conception of the 3-adic unit disc" by A. T. Fomenko, included as frontispiece in Neal Koblitz' book, $p$-adic Numbers, $p$-adic Analysis, and Zeta-Functions.