Let $P\subset\Bbb R^d$ be a convex polytope (a convex hull of finitely many points). Lets call it flexible, if it can be continuously deformed while
- keeping its combinatorial type, and
- keeping its edge-lengths.
I know that the $d$-cube is flexible in this sense. More generally, most (all?) zonotopes are flexible (see the comments). Also all polygons are flexible. But are there any others?
$\quad\quad$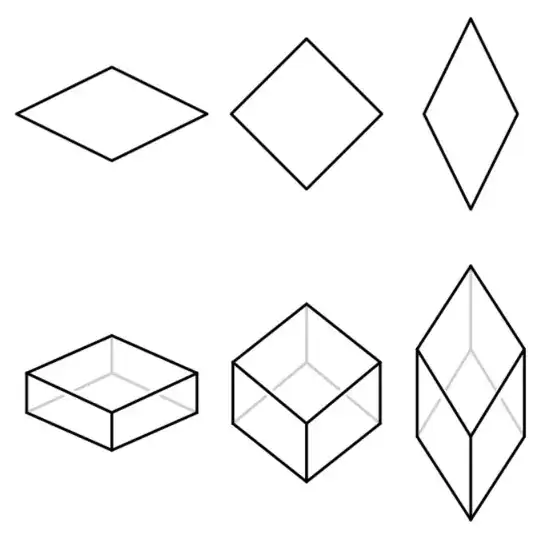
I also know that there are polytopes having several realizations with matching edge-lengths (e.g. see the image here), but these realizations cannot be continuously deformed into each other while preserving all edge-lengths.