2

Given $u\in\mathbb{C}$ and $v\in\mathbb{C}$ let's consider the following progression: $$z_n=u+nv\;\;\;\;\;\;\;\;\;n\ge 0$$

Is it possible to find progressions $z_n$ generating gaussian primes for an arbitrary long sequence of consecutive values of n?

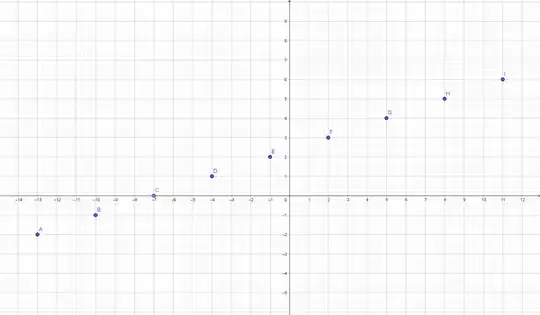
For example, $z_n=-13-2i+n(3+i)$ generates gaussian primes for all values $0\le n\le 8$ (examine the norm $|z_n|^2=10n^2-82n+173$):

enter image description here

If not, it is known the progression of maximum lenght?

Many thanks.

Augusto Santi
  • 1,000
  • @StanleyYaoXiao Your claim about Gaussian primes is false (3 is a Gaussian prime, but its norm is 9). – David Loeffler Aug 20 '20 at 19:48
  • @DavidLoeffler I was working under the supposition that only primes that split in $\mathbb{Z}[i]$ count as "Gaussian primes", which I believe is intended by the question (typically the expression $u + nv$ given in the question will never equal a rational integer). I can edit the comment to clarify this – Stanley Yao Xiao Aug 20 '20 at 19:50
  • Since a Gaussian integer $x = a + ib$ with $ab \ne 0$ is prime if and only if its norm is a rational prime, your question is equivalent to asking for fixed Gaussian integers $u,v$ whether exist infinitely many rational integers $n$ such that the expression $|u|^2 + 2n\Re(u\overline{v}) + n^2 |v|^2$, which is a quadratic polynomial in $n$ with rational integer coefficients, is prime infinitely often. There is no irreducible quadratic polynomial for which we know the answer. – Stanley Yao Xiao Aug 20 '20 at 19:51
  • Your assertion is still false -- what about 3i? Moreover, where in the question is it specified that $u, v$ can't be rational integers? – David Loeffler Aug 20 '20 at 19:53
  • @DavidLoeffler it doesn't, but inferring from the example given and the assumption that the OP understands how to count arithmetic progressions in the rational primes (which is what one gets if $u,v$ are co-prime rational integers and $n$ a rational integer parameter), I believe it is reasonable to assume that $u,v$ are not rational integers nor of the form $\pm ix$ for rational integral $x$. – Stanley Yao Xiao Aug 20 '20 at 19:57
  • That wasn't the question that was asked. Moreover, you seem to be confusing "there is an arithmetic progression containing infinitely many primes" with "there are arbitrarily long (finite) arithmetic progressions consisting only of primes" – David Loeffler Aug 20 '20 at 20:03

2 Answers2

6

The Green--Tao theorem also shows that there are arbitrarily long arithmetic progressions among the (rational) primes that are congruent to 3 modulo 4. See for instance this MO question Is the Green-Tao theorem true for primes within a given arithmetic progression?.

Since any rational prime that is 3 mod 4 is a Gaussian prime, this shows that the Gaussian primes contain arbitrarily long arithmetic progressions.

(This is perhaps a slightly unsatisfactory class of examples. I don't know if there are arbitrarily long arithmetic progressions of primes in $\mathbf{Z}[i]$ which aren't in $\mathbf{Z}$ or $i \mathbf{Z}$.)

David Loeffler
  • 36,132
  • 2
    A theorem of Tao https://arxiv.org/abs/math/0501314

    says: given any finite sets of points $v_i \in \mathbb{Z}[i]$ there are infinitely many $a \in \mathbb{Z}[i], r \in \mathbb{Z}\setminus {0}$ such that all $a+rv_i$ are Gaussian primes. Choosing a shape of two parallel lines, say $v_{1,j}=j, v_{2,j}=i+j, j\in {1, \ldots , k}$, shows that there are also long progressions of Gaussian primes not all on the real line, which answers the question left open by David. One could also take lines, say, with 45 degrees angle.

     – Christian Elsholtz Aug 21 '20 at 07:28
  • 2
    You should post that as an answer, it's great – David Loeffler Aug 22 '20 at 08:40
2

A theorem of Tao arxiv.org/abs/math/0501314 says: given any finite sets of points $v_i \in \mathbb{Z}[i]$ there are infinitely many $a\in \mathbb{Z}[i],r\in \mathbb{Z}\setminus \{0\}$ such that all $a+rv_i$ are Gaussian primes. Choosing a shape of two parallel lines, say $v_{1,j}=j,v_{2,j}=i+j,j\in \{1, \ldots,k\}$, shows that there are also long progressions of Gaussian primes not all on the real line, (which also answers the question left open by David). One could also take lines, say, with 45 degrees angle.

Christian Elsholtz
  • 2,725