Why do bees create hexagonal cells ? (Mathematical reasons)

Question

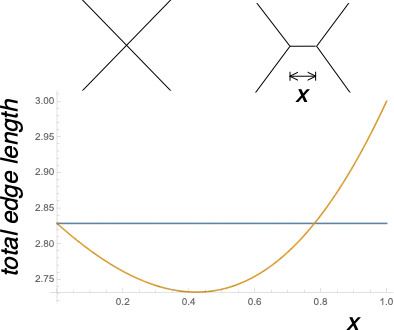
Question 0 Are there any mathematical phenomena which are related to the form of honeycomb cells?

Question 1 Maybe hexagonal lattices satisfy certain optimality condition(s) which are related to it?

The reason to ask - some considerations with the famous "K-means" clustering algorithm on the plane. It also tends to produce something similar to hexagons, moreover, maybe, ruling out technicalities, hexagonal lattice is optimal for K-means functional, that is MO362135 question.

Question 2 Can it also be related to bee's construction?

---

Googling gives lots of sources on the question. But many of them are focused on non-mathematical sides of the question - how are bees being able to produce such quite precise forms of hexagons? Why is it useful for them? Etc.

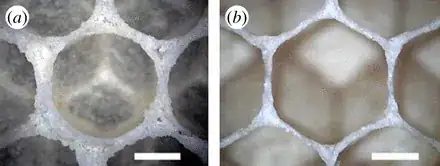
Let me quote the relatively recent paper from Nature 2016, "The hexagonal shape of the honeycomb cells depends on the construction behavior of bees", Francesco Nazzi:

Abstract. The hexagonal shape of the honey bee cells has attracted the attention of humans for centuries. It is now accepted that bees build cylindrical cells that later transform into hexagonal prisms through a process that it is still debated. The early explanations involving the geometers’ skills of bees have been abandoned in favor of new hypotheses involving the action of physical forces, but recent data suggest that mechanical shaping by bees plays a role. However, the observed geometry can arise only if isodiametric cells are previously arranged in a way that each one is surrounded by six other similar cells; here I suggest that this is a consequence of the building program adopted by bees and propose a possible behavioral rule ultimately accounting for the hexagonal shape of bee cells.

Answer 1

There are two principles at play here: a mathematical principle that favors hexagonal networks, and a physical principle that favors a network with straight walls.

The mathematical principle that prefers hexagonal planar networks is Euler's theorem applied to the two-torus $\mathbb{T}^2$ (to avoid boundary effects), $$V-E+F=0,$$ with $V$ the number of vertices, $E$ the number of edges, and $F$ the number of cells. Because every vertex is incident with three edges$^\ast$ and every edge is incident with two vertices, we have $2E = 3V$, hence $E/F=3$. Since every edge is adjacent to two cells, the average number of sides per cell is 6 --- hence a uniform network must be hexagonal.

_{$^\ast$ A vertex with a higher coordination number than 3 is mechanically unstable, it will split as indicated in this diagram to lower the surface energy.}

_{blue: total edge length for the left diagram (diagonals of a unit square), gold: total edge length for the right diagram, as a function of the length $x$ of the splitting.}

Euler's theorem still allows for curved rather than straight walls of the cells. The physical principle that prefers straight walls is the minimization of surface area.

_{source: Honeybee combs: how the circular cells transform into rounded hexagons}

An experiment that appears to be directly relevant for honeybee combs is the transformation of a closed-packed bundle of circular plastic straws into a hexagonal pattern on heating by conduction until the melting point of the plastic. Likewise, the honeybee combs start out as such a closed-packed bundle of circular cells (panel a). The wax walls of the cells are heated to the melting point by the bees and then become straight to reduce the surface energy (panel b).

Answer 2

There is this theorem of Thomas Hales from 1999, which proves the Honeycomb Conjecture:

Theorem. Let $\Gamma$ be a locally finite graph in $\mathbb{R}^2$, consisting of smooth curves, and such that $\mathbb{R}^2\setminus \Gamma$ has infinitely many bounded connected components, all of unit area. Let $C$ be the union of these bounded components. Then $$ \limsup_{r \to \infty} \frac{ \mathrm{perim}\, (C \cap B(0, r))}{\mathrm{area}\, (C \cap B(0, r))} \geq \sqrt[4]{12} $$ Equality is attained for the regular hexagonal tiling.

So basically it is optimal way to partition the plane into cells of equal area using least amount of perimeter. This doesn't account for the fact that honeycomb lattice is 3d and not exactly cylindrical with hexagonal cross section.

The paper introduction has a bit of discussion https://arxiv.org/abs/math/9906042

Answer 3

Isn't it just the 2d sphere packing? If one assumes that the larvae needs a disc of fixed radius to grow up to an adult form and that the bees want to have as many cells as possible then the hexagonal lattice is the optimal one.

Answer 4

Here is a classic article by L. Fejes Toth on this subject.

https://projecteuclid.org/euclid.bams/1183526078

Answer 5

Here is a paragraph of THE LIFE OF THE BEE (1901) By Maurice Maeterlinck:

"There are only," says Dr. Reid, "three possible figures of the cells which can make them all equal and similar, without any useless interstices. These are the equilateral triangle, the square, and the regular hexagon. Mathematicians know that there is not a fourth way possible in which a plane shall be cut into little spaces that shall be equal, similar, and regular, without useless spaces. Of the three figures, the hexagon is the most proper for convenience and strength. Bees, as if they knew this, make their cells regular hexagons.

"Again, it has been demonstrated that, by making the bottoms of the cells to consist of three planes meeting in a point, there is a saving of material and labour in no way inconsiderable. The bees, as if acquainted with these principles of solid geometry, follow them most accurately. It is a curious mathematical problem at what precise angle the three planes which compose the bottom of a cell ought to meet, in order to make the greatest possible saving, or the least expense of material and labour.* This is one of the problems which belong to the higher parts of mathematics. It has accordingly been resolved by some mathematicians, particularly by the ingenious Maclaurin, by a fluctionary calculation which is to be found in the Transactions of the Royal Society of London. He has determined precisely the angle required, and he found, by the most exact mensuration the subject would admit, that it is the very angle in which the three planes at the bottom of the cell of a honey comb do actually meet."

Terry Tao and Allen Knutson have some papers about application of Honeycomb in math:

Knutson, Allen; Tao, Terence, The honeycomb model of $\text{GL}_n(\mathbb C)$ tensor products. I: Proof of the saturation conjecture, J. Am. Math. Soc. 12, No. 4, 1055-1090 (1999). ZBL0944.05097.

Knutson, Allen; Tao, Terence, Honeycombs and sums of Hermitian matrices., Notices Am. Math. Soc. 48, No. 2, 175-186 (2001). ZBL1047.15006.