I'm not sure I understood the question and answer given by the asker, but I gather that they are interested in decidability questions about some substitutive subshifts.
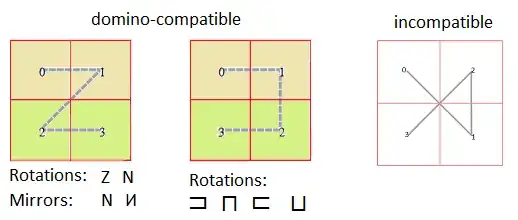
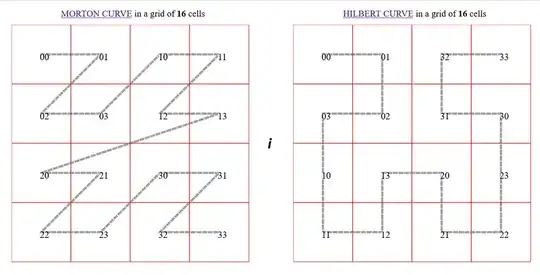
As far as I can tell, the questions about which dominoes occur more often are in general solved by basic linear algebra; when you have a substitution giving the tiling you just compute some eigenvectors for its abelianization, not really on-topic for this site. In the case of the two example substitutions the solutions are already given by the asker; I don't know what "empirical induction" is, but the facts that horizontal and vertical dominoes appear with the same frequency in Hilbert, and all are horizontal in the other one, can be proved by induction. That said, let me concentrate on aperiodicity, which is more interesting.
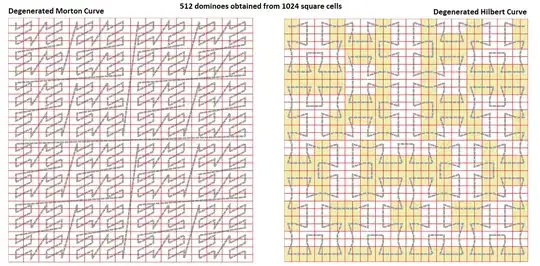
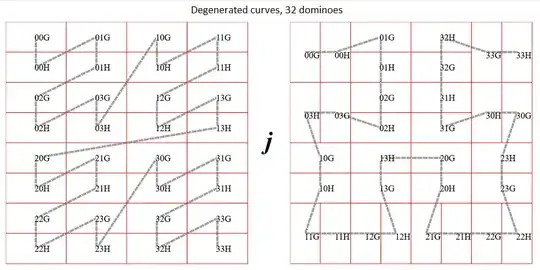
I'll give some basic info about that: for any substitutive curve, the aperiodicity question about its dominofied version is decidable (if the class being implied is anything like I think). I didn't actually get what the degenerated stuff was about, but seems to be about some projections or factor images as well, so should be covered by the general theory. I also give a more classical style symbolic dynamics proof that the dominofication of the Hilbert curve is a minimal aperiodic subshift.
Aperiodicity is decidable: an automata theory proof
First, some definitions. Let $m, n \in \mathbb{N}$, $A$ a finite alphabet and $\tau : A \to A^{m \times n}$ a function. We interpret $\tau$ as replacing $a \in A$ by an $m \times n$ matrix, and we call such $\tau$ a ($m$-by-$n$)-substitution. We can apply $\tau$ to $P \in A^{k \times \ell}$ to obtain $\tau(P) \in A^{km \times \ell n}$, in the obvious way by replacing the individual elements of $A$ with $m \times n$ matrices.
If $\tau$ is a substitution, we say a (one-sided) infinite configuration $x \in A^{\mathbb{N}^2}$ is a $\tau$-periodic point if $\tau^k(x) = x$ for some $k > 0$, where we apply a substitution to an infinite configuration $x$ in an obvious way (the origin stays put, everything else blows up in the positive direction). We can find natural $\tau$-periodic points as follows: Start with a symbol $a \in A$, and keep applying $\tau$. The symbol $\tau^n(a)|_{(0,0)}$ evolves eventually periodically, say with some eventual period $p$. Then $\tau^{p\ell}(a)$ actually tends to a limit in an obvious sense (cellwise), and this limit is $\tau$-periodic as an infinite configuration (with period $p$).
Say $x \in A^{\mathbb{N}^2}$ is $n$-automatic if for all $a \in A$, the set $\{v \in \mathbb{N}^2 \;|\; x_v = a\}$ is $n$-automatic. A set of pairs of numbers $N \subset \mathbb{N}^2$ is $n$-automatic if the language $L_n$, of words $w \in (\{0,1,...,n-1\}^2)^*$ which evaluate to a pair of numbers in $N$ when you separately read off the $n$-ary numbers on the two tracks, is a regular language. Regular languages are very robust so I won't give the precise formulas, you can't really guess them wrong. We similarly define $n$-automatic configurations in $A^{\mathbb{N}^d}$ and subsets of $\mathbb{N}^d$.
The following is relatively easy to show, you can find it (or at least its one-dimensional version) in many references and books that discuss automata and substitutions.
Theorem. Let $\tau : A \to A^{n \times n}$ be a substitution and let $x$ be any $\tau$-periodic point. Then $x$ is $n$-automatic.
The proof is not very hard, the idea is the automaton just keeps track of the current symbol and when it reads a digit, that tells it where it moves in the substitutive image (and it looks up $\tau$ to see which symbol is there).
The following is obvious by basic closure properties of regular languages.
Lemma. Let $x \in A^{\mathbb{N}^2}$ be $n$-automatic, and $\pi : A \to B$ a function. Then $\pi(x) \in B^{\mathbb{N}^2}$, defined by $\pi(x)_v = \pi(x_v)$, is also $n$-automatic.
The following is classical, perhaps first invented by Büchi. There is an implementation called Walnut where you can directly input such statements. I get the impression the asker is into computers, so I'll leave it as an exercise to try this out (sometimes Walnut cracks very difficult problems, sometimes it gets stuck on very trivial things, it's all about whether the intermediate DFAs happen to have huge numbers of states, which is hard to predict). The decidability proof is not so hard, the idea is to do quantifier elimination by using the subset construction.
Theorem. Let $x \in A^{\mathbb{N}^2}$ be $n$-automatic, and let $\phi$ be any first-order formula (with constants and free variables) where quantifiers range over vectors in $\mathbb{N}^2$, and you have function sumbols for vector addition, and have a unary predicate for "$x_v = a$" for each $a \in A$, with the obvious interpretations. Then the set of solutions to $\phi$ (possible values for the free variables) are an $n$-automatic subset of $\mathbb{N}^d$, which can be computed effectively; if there are no free variables, whether $\phi$ is a true statement is decidable.
Now, the question of aperiodicity amounts to programming in first-order logic. We say $x \in A^{\mathbb{N}^2}$ is aperiodic if its stabilizer $\{v \in \mathbb{N}^2 \;|\; v+x = x\}$ is trivial, where $v+x$ denotes translation $(v+x)_u = x_{v+u}$. This is not to be confused with $\tau$-periodicity.
Lemma. A configuration $x \in A^{\mathbb{N}^2}$ is aperiodic if and only if it satisfies the following first-order statement (of the type in the previous theorem):
$$ \forall v \neq 0: \exists u: x_{u+v} \neq x_u. $$
Hopefully no need for a proof, since basically I just wrote the definition. This lemma and formula are about periodicity of a full $\tau$-periodic quarterplane, but you can modify the formula to talk about arbitrarily large periodic areas, or periodicity up to skipping some initial rows and columns, or many other things, it's just first-order formula programming. Now, I believe the following theorem solves a relatively general version of your question:
Theorem. For any substitution $\tau : A \to A^{n \times n}$, any $\tau$-periodic $x \in A^{\mathbb{N}^2}$, and any map $\pi : A \to B$, it is decidable whether the configuration $\pi(x)$ is aperiodic.
Proof: We have that $x$ is $n$-automatic, thus $\pi(x)$ is $n$-automatic, and it is decidable whether the formula of the previous lemma is true, thus it is decidable whether $\pi(x)$ is aperiodic. Square.
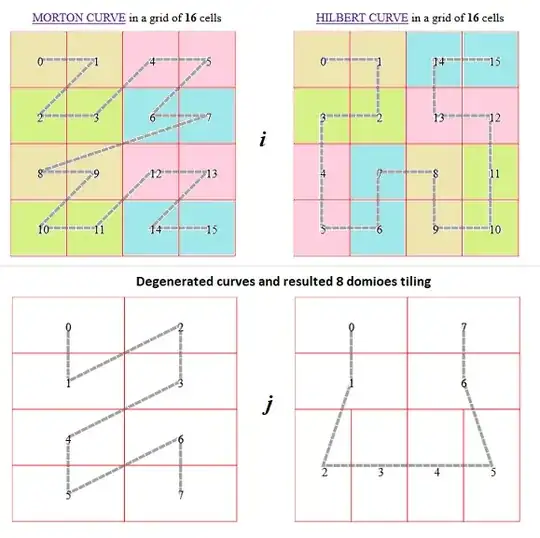
Now, we can solve your Hilbert curve question as follows:
Take as alphabet the symbols for the cardinal directions $\{ N, E, W, S \}$, which represent the different directions where a basic "$U$-shape/$U$-curve" of the Hilbert curve (by which I mean one of the length-$4$ segments from which the curve consists) may open. Take the Cartesian product with $\{-1, 0, 1\}$ as there are three different ways the curve may continue from the first and last point of the curve (either it continues straight or turns, and it never goes straight from both ends). You can then work out a substitution on $12$ symbols, which carries all the relevant information. (It's a reasonable coding, since it's easy to see that you can tell from a dominofied configuration which are the $2$-by-$2$ blocks coming from a basic $U$-shape.) The map $\pi$ takes $\{N, E\}$-type symbols to $V$ and $\{W, E\}$-type symbols to $H$ (ignoring the $\{0, 1, 2\}$ component).
For example, if $-1$ means "turn on the left", $1$ means "turn on the right" and $0$ means "turn on both ends", then
$$ \tau(N, 0) = \begin{pmatrix} (W, -1) & (E, 1) \\ (N, 1) & (N, -1) \end{pmatrix}. $$
This is the example you give, but I carry the additional information of how the curve would continue, and I do not yet do the final substitutions where you actually write the basic $U$-curves, and where you then substitute them for a pair of dominoes.
So there's an algorithm that solves whether the Hilbert curve domino thingie is aperiodic. I did not run it, and do not claim it's very efficient. Instead...
Aperiodicity of the Hilbert curve: a symbolic dynamics proof
I'll give a manual proof (I did check the combinatorics in Python, but it's my native language so that's much less work than Walnut, and I think it shouldn't be hard to work out on pencil-and-paper).
Now, let me describe another way, which is what people usually do in practice (because it's more fun to do this way when working manually), and then I can give a quick manual proof that the Hilbert curve gives you an aperiodic domino tiling. We are going to replace computation with more conceptual ideas, so we need more definitions.
A subshift is a subset $X \subset A^{\mathbb{Z}^2}$ which is topologically closed in the profinite (Cantor) topology, and is shift-invariant meaning $\forall x \in X: \forall v \in \mathbb{Z}^2: v+x \in X$. (I move to $\mathbb{Z}^2$-configurations form $\mathbb{N}^2$-configurations for convenience, but actually after the topologization everything will turn into questions about finite objects, so this will not matter much.)
If $x \in A^{\mathbb{Z}^2}$ and $P \in A^{k \times \ell}$, write $P \sqsubset x$ for $P$ appearing somewhere in $x$, i.e. $\exists v \in \mathbb{Z^2}: (v+x)|_{k \times \ell} = P$, where $v+x$ denotes translation $(v+x)_u = x_{v+u}$. Similarly we write $P \sqsubset Q$ for $P$ appearing somewhere in $Q$ when $P \in A^{m \times n}$ and $Q \in A^{k \times \ell}$, with the obvious meaning. The subshift generated by $\tau$ from $a \in A$ is the set of all $x \in A^{\mathbb{Z}^2}$ such that for any $k, \ell$ and any such that $P \sqsubset x$, there exists $n$ such that $P \sqsubset \tau^n(a)$.
We also reformulate $\tau$-periodicity for $\mathbb{Z}^2$-configurations. We say $x \in A^{\mathbb{Z}^2}$ is a good $\tau$-periodic point if there exists $R \in A^{2 \times 2}$ such that $R$ appears in $\tau^n(a)$ for some $a \in A$, $n \in \mathbb{N}$, and $x$ is the limit of $R$ obtained by taking the limits $\tau^p(b)$ of the four symbols in $R$ separately, for some $p \in \mathbb{N}$, i.e. each of them separately expands into its own direction. Such $\tau$-periodic configurations again exist by the pigeonhole principle since the set of $2$-by-$2$ patterns is finite.
If $\tau$ is a substitution, write $M_\tau$ for the $|A|$-by-$|A|$ matrix where $(M_\tau)_{a,b} = |\{k \;|\; \tau(a)_k = b\}|$, i.e. rows tell you how many of each symbol appears in each $\tau$-image. We say a matrix $M$ is primitive if there exists $n$ such that $M^n$ has only positive entries. We have that $M_\tau$ is primitive if and only if $b \sqsubset \tau^n(a)$ for any choice $a, b \in A$, and we then also say $\tau$ is primitive.
The following lemma can be found in any reference that discusses substitutions (at least its one-dimensional version, but it's exactly the same in two dimensions since our substitution is rectangle-shaped).
Let $\tau$ be a substitution such that $M_\tau$ is primitive. Then the subshift $X$ generated from $a$ does not depend on the choice of $a$, and the orbit-closure of every good $\tau$-periodic point is $X$. The subshift $X$ is minimal, i.e. the orbit-closure of every point in $X$ is $X$.
By this lemma, and the easily proved fact that the Hilbert curve substitution is primitive, we don't really have to worry about whether things are one-sided or two-sided: minimality means that either every configuration $x \in X$ satisfies $v+x = x$ for some $v \in \mathbb{Z}^2 \setminus \{(0,0)\}$ independent of $x$, or for all $v \in \mathbb{Z}^2 \setminus \{(0,0)\}$ there exists $m$ such that the $v$-periodic is locally broken in all patterns of size $m$-by-$m$ that appear when you iterate this substitution.
A morphism from subshift $X$ to subshift $Y$ is a continuous function $\pi : X \to Y$ which commutes with the shift maps, i.e. $\pi(v+x) = v + \pi(x)$ for all $x \in X$, $v \in \mathbb{Z}^2$. It is easy to see that being aperiodic is preserved under a morphism.
Now, we proceed as follows: Let $X$ be the subshift generated by the Hilbert curve substitution $\tau$.
- Define the map $\pi : \{N,E,W,S\} \times \{-1,0,1\} \to \{N,E,W,S\}$, which drops the information about how the curve continues, let the image be $Y$, so we have a morphism $\pi : X \to Y$.
- Show that $Y$ is aperiodic.
- Show that the map $\pi' : \{N,E,W,S\} \to \{H,V\}$, which extracts the dominoes, is an isomorphism onto its image, denote it as $\pi' : Y \to Z$.
- Now, $Z$ has to also be aperiodic, because the inverse $(\pi')^{-1} : Z \to Y$ would preserve any period.
We first show that $Y$ is aperiodic. To see this, we observe that actually we could have in the first place defined the Hilbert curve substitution $\tau$ without using the curve information (I just included it to keep it as close to the original description as possible; I didn't check whether $\pi$ is an isomorphism): $Y$ is the subshift given by the substitution $\tau'$ obtained from $\tau$ that ignores the curve information completely (again $\tau'$ is primitive so $Y$ is minimal).
I proved the aperiodicity as follows: the pattern
$\begin{pmatrix} N & W & E & N \\ S & W & E & S \end{pmatrix}$
can only appear in only even positions of substituted images of patterns (both coordinates even), as you can see by analyzing $(\tau')^n(R)$ for small $n$ and $2$-by-$2$ patterns $R$ ($n = 3$ is enough). Since $\tau'$ is injective, you can "use a local rule to detect whether a given $2$-by-$2$ block you see is actually a substituted image of a symbol, or whether it appears between two such images, in a unique way" (one says the subshift recognizable in the sense of Mossé).
Let me not define that because I don't know a particularly neat way to do that, but you can find this in any reference that discusses recognizability and substitutions. Instead, let me intuitively explain what we do with this local rule: once you can figure out which $2$-by-$2$ blocks come from symbols, in fact by the substitutive nature of the subshift the preimages of these blocks form a configuration of the same subshift $Y$. So you can iterate the local rule, and what you get once you forget all but the "phases" is a continuous shift-invariant map $\phi : Y \to I^2$, where $I$ the $2$-adic integers, and where $\mathbb{Z}^2$ acts on $I^2 = I \times I$ by translation ($\mathbb{Z} \leq I$ is a dense subgroup; the dynamical system $I$ is usually called the $2$-adic odometer). Since $I^2$ is a torsion-free group, $I^2$ under the translation action of $\mathbb{Z}^2$ has only aperiodic points, and thus so must $Y$ (morphisms between general dynamical systems also preserve periods).
Finally, we need to show that map $\pi' : Y \to Z$, is an isomorphism. For this, we argue similarly as above: A short case analysis shows that the pattern
$$ \pi'(\tau'(\begin{pmatrix} W & E \\ N & N \end{pmatrix})) = \begin{pmatrix} V & H & H & V \\ V & H & H & V \\ H & H & H & H \\ V & V & V & V \end{pmatrix} $$
only appears in even positions (both coordinates even), among the patterns $\pi'(\tau'^n(a)$ for any $n$ and $a \in A$. This again gives us a unique $2$-by-$2$ phase. We observe that $\pi'$ is injective on the $\tau'(A)$ so we can deduce the preimage configuration completely, proving $\pi' : Y \to Z$ is actually an isomorphism.
So as discussed earlier, the subshift $Z$ which is the dominofication of the Hilbert curve subshift, must be aperiodic (i.e. every configuration is aperiodic in it). It is also minimal as it is a morphic image of $Y$.