Either intentionally or unintentionally. Include location and sculptor, if known.
-
9Coincidentally or not, an article on mathematical sculpture just came out in the AMS Notices: http://www.ams.org/notices/201007/rtx100700840p.pdf – Charles Staats Jul 19 '10 at 13:24
-
8There is absolutely no reason to close this beautiful (literally) question. – Gil Kalai Nov 14 '13 at 21:13
43 Answers
The Mathematical Research Institute in Oberwolfach have a sculpture on their grounds depicting Boy's surface:

(source: mfo.de)

- 2,743
- 2,517
-
It was a gift of the Mercedes-Benz... but is there an artist who made it? – Pietro Majer Jul 19 '10 at 13:47
-
I don't read German, perhaps in the linked article here http://www.mfo.de/general/boy/ there's an answer? – Willie Wong Jul 19 '10 at 13:50
-
The article seems to say that it was produced by a computer-aided-manufacturing system at Mercedes-Benz, rather than an artist. – Jul 20 '10 at 10:01
-
6so, remarkably, the most appeciated sculpture here was made by a computer? – Pietro Majer Jul 20 '10 at 16:34
-
39Well, many sculptures, even when "made by an artist" were in fact made after the artist programmed it into a computer, which then did the work. We don't say that other works were "made by a chisel" or "made by a paintbrush" do we? – Gerald Edgar Mar 13 '11 at 13:21
Helaman Ferguson. My department has one of these in the main office:

(source: helasculpt.com)
Keizo Ushio. He made this during the 2006 ICM in Madrid: 
(source: memenet.or.jp)
- 2,743
- 5,776
-
1
-
There is also a paper, Friedman and Sequin, Keizo Ushio’s Sculptures, Split Tori and Möbius Bands, available at http://www.maths.ed.ac.uk/~aar/papers/keizo.pdf – Gerry Myerson Nov 10 '13 at 23:09
-
Being able to watch, while entering the conference centre, Keizo Ushio either sculpting with his power tools or standing thinking was one of the highlights of the 2006 ICM. – IJL Sep 22 '22 at 18:51
The centrepiece of McAllister building, which houses the math department at Penn State, is the Octacube, designed by Adrian Ocneanu.

There's a bit of a description of the mathematics behind the Octacube on the Penn State website, but unfortunately, that's the most material that I can find online. There are all kinds of animations set up to display on a computer terminal in McAllister building, but they don't seem to be available online anymore.
Very briefly, the mathematics of the sculpture is as follows: consider the four-dimensional regular convex polytope whose vertex set is the union of the vertex sets for the four-dimensional cube {(±1,±1,±1,±1)} and the four-dimensional octahedron {(±2,0,0,0), (0,±2,0,0), (0,0,±2,0), (0,0,0,±2)}. Consider the 1-skeleton of this polytope (vertices and edges), and project radially to S3 ⊂ ℝ4. Project the resulting "inflated polytope" stereographically to ℝ3, and "fatten" the edges so that a cross-section of an edge is no longer just a point, but a Y-shape (see the corners of the sculpture). What you get is the sculpture shown.
- 8,782
-
-
Oops... I absolutely do. Fixed it in the post... thanks for the correction. – Vaughn Climenhaga Jul 19 '10 at 19:23
MoMath, in partnership with Make, has a regular feature on DIY math sculptures. I personally like the space filling curve made of steel pipe ells by Chaim Goodman-Strauss and Eugene Sargent.

- 5,926
A model of the Riemann zeta function suggesting the zeroes and pole. One of several models at the University of Regensburg Math Dept.
3-D Permutahedron Sundial by Stefano Buonsignori (16th century) in the Medici collection presented by Museo Galileo. The 3-D permutahedron:
(The combinatorics underlying the geometry of the permutahedra are related to multiplicative inversion and, consequently, to Koszul duality and the formalism of Appell sequences and associated matrices, so I find this particular jewel at the juncture of art, engineering, geometry, combinatorics, and analysis particularly exciting. If only he had done one for the associahedron!)
Calabi-Yau space: the shape of the inner space of the universe. In Yau's hometown in south China.
See 3-D animation in "Where math meets physics" by Brockmeier, also intro in "Hidden dimensions" by Freiberger and the survey "The Calabi-Yau Landscape:from Geometry, to Physics, to Machine-Learning" by Yang-Hui He.
Eversion of a sphere: Models in resin made by Stewart Dickson of clay models made by Bernard Morin (a blind topologist!) of different stages of the eversion of a sphere. The resin models were presented at the Maubeuge symposium "Arts et Mathématiques." (Photo by John Sullivan.)
Excerpt (p. 146) from "Poincare's Prize" by G Szipiro:
(Smale) proved a theorem that showed it is possible to evert the sphere. But the procedure implicit in his theorem was so complicated that nobody could visualize it. Smale, and others who tried, wanted to see with their own eyes how the sphere would evert. For once, the ability to visualize may actually have been a handicap. It was left to the blind mathematician Bernard Morin to devise a procedure to turn a sphere inside out that could actually be implemented (if the membrane is able to pass through itself, that is.)
A sculpture by Gideon Weisz of an approximation of Alexander's horned sphere to five levels.
(Photo from “The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes” by David Darling.)
'Tripartite unit' [Unidade Tripartida], Max Bill
This sculpture is topologically equivalent to the connected sum of three projective planes with a point removed, corresponding to the only boundary component of the represented surface.
Isometric transformation between a catenoid and helicoid
Presented at the 2019 Mathematical Art Exhibition held at the AMS Joint Mathematical Meetings in Baltimore, MD. (30 x 25 x 25 cm, paper, mdf, steel, magnet, 2018.)
To the left is a paper-crafted catenoid, and to the right, a helicoid. These surfaces can be transformed isometrically into each other, i.e., without any strain, because the first fundamental form of the surfaces are identical.
I made this model by weaving together paper strips whose shapes were obtained by minimizing the strain energy defined on a Riemannian manifold. The optimization problem was solved numerically using NURBS-based isogeometric analysis.
- Yuto Horikawa
Dandelin spheres (description)
Clebsch diagonal surface (description)
The two models above are part of the M. Schelling Collection of the Geometric Models Collection at V. N. Karazin Karkiv National Univ. (See historical notes for the collection and in comments below.)
Fermi surface of copper with permutohedral Brillouin zone
As Kaganov and Lifshitz put it, the Fermi surface is‘the stage on which the ‘drama of the life of the electron’ is played out. -- Dugdale from Life on the edge: a beginner’s guide to the Fermi surface
See also "The Magic Wand Theorem of A. Eskin and M. Mirzakhani" by Zorich
Gates to the Center for Mathematical Studies at Cambridge
From "What is ... a Skein Module" by Lickorish:
Mathematical Gates. The main entrance to the Centre for Mathematical Sciences in Cambridge is sealed by iron gates. Medallions in these gates show the only two knots with at most eleven crossings, other than the unknot, that have trivial Alexander polynomial. One gate shows the knot studied by S. Kinoshita and H. Terasaka, whilst the other gate shows the knot discovered by J. H. Conway in his classification of eleven-crossing knots. Related as they are by one of Conway’s mutations they cannot be distinguished by any invariant based on skein theory. The medallions were created by John Robinson and donated by Damon de Laszlo and Robert Hefner III.
Dodecahedron at Burning Man
From Satayan L. Devadoss:
UNFOLDING HUMANITY: BURNING MAN (2018)
A two-ton metal, wood, and acrylic interactive sculpture, showcasing unsolved problems of mathematics, came to life in the middle of the Nevada desert. Rising 12 feet tall with an 18-foot wingspan, the unfolding dodecahedron was externally skinned with black panels containing 2240 acrylic windows, illuminated by over 16,000 LEDs which were programmed and driven by 20 controllers. The interior, large enough to hold 15 people, was fully lined with a massive mirror over each of the twelve pentagonal faces.
Our motivating question asks, what could it look like for vibrant and unsolved mathematics to be made embodied and physical, to engage the general public? And so, this sculpture deals with two unsolved questions: the unknown possibility of unfolding any convex polyhedra (motivated by 500-year-old works of Albrecht Dürer) and the shape of our universe (from WMAP cosmic microwave background radiation data and the Poincaré dodecahedral space).

3-D Projection of a 4-D Associahedron
A metal skeletal framework created by Eric Jonash and Sam Kapala via truncations of successively higher dimensional cells of the 4-simplex. See See Figs. 3.14 on pg. 76 and 7.28 on pg. 241 of Discrete and Computational Geometry by Devadoss and O'Rourke. "The vertices of this polytope correspond to all ways of triangulating the regular seven-gon, and the edges connect two such triangulations related by a flip."--Devadoss at link above.
A Seifert Surface Bordered by Borromean Rings
This surface has three edges, each a simple closed loop, which are locked together in an ancient form called the Borromean Rings. Named after its use in an Italian coat of arms, these three rings are locked together inextricably although no two of them are linked. Their Seifert surface twists through the loops smoothly and gracefully, ... . -- Bathsheba Sculpture
See also J. van Wijk's Visualization of Seifert Surfaces.
- 9,937
-
For more info on the instrument, see http://hsm.stackexchange.com/questions/5573/inscriptions-on-a-16th-century-3-dimensional-permutahedron-sundial. – Tom Copeland Jan 14 '17 at 00:49
-
-
H. Weyl: Klein put a special enphasis on geometrical and physical intuition, which he managed to develop in the students by letting them construct solid (plaster, or metal) models of curves and surfaces in ordinary 3-space, or letting them draw very broad (1 x 2 meters) paper tables of cubic plane curves with an explicit plotting of their Q-rational points. A concrete witness to this tradition is the exhibition of plaster models of surfaces which are to be found still nowadays in the Halls of the Mathematical Institute in Gottingen. – Tom Copeland Feb 05 '20 at 22:39
-
(cont.) These models were then produced by the publishing company L. Brill in Darmstadt, later by the Schilling publishing company, and sold around the world: I have personally seen many of those in most of the older Deparments I have visited (cf. the 2 Volumes edited by G.Fischer on ”Mathematical Models” ... . // Writes G. Fischer : There were certainly other reasons than economic for the waning interest in models. ... . More and more general and abstract viewpoints came to the forefront of mathematics ... . Finally Nicolas Bourbaki totally banned pictures from his
books. – Tom Copeland Feb 05 '20 at 22:41 -
3Some of those sculptures look remarkably like extremely uncomfortable chairs/benches. – nomen Feb 05 '20 at 23:19
-
2@nomen, lol, maybe that's the underlying, motivating sentiment of the Bourbakists. – Tom Copeland Feb 05 '20 at 23:28
-
1Klein and Fischer quotes above are from "From Abel's heritage: Transcendental objects in algebraic geometry and their algebrization"" by Catanese. – Tom Copeland Feb 05 '20 at 23:40
-
On Alexander's horned sphere, see https://lamington.wordpress.com/2017/04/08/bings-wild-involution/ – Tom Copeland Feb 25 '20 at 23:07
-
On Caliba-Yau space, see "From Strings to Mirrors" a AMS feature column by Ursula Witcher https://www.ams.org/publicoutreach/feature-column/fc-2020-03 – Tom Copeland Mar 02 '20 at 18:55
-
Some sculptures presented at https://www.ams.org/publicoutreach/math-imagery/ICERM-2019 – Tom Copeland Mar 11 '20 at 20:16
-
Ghys in "A Singular Mathematical Promenade" has some photos of models related to Riemann surfaces at the Göttingen Collection of Mathematical Models and Instruments. – Tom Copeland Mar 11 '20 at 20:27
-
Some photios of models at Gottingen: https://www.atlasobscura.com/places/the-gottingen-collection-of-mathematical-models-gottingen-germany – Tom Copeland Mar 11 '20 at 20:34
-
Get your own Calibi-Yau model https://www.shapeways.com/product/PYRPYTHGT/calabi-yau – Tom Copeland Apr 28 '20 at 17:21
-
"Modeling Dynamical Systems for 3D Printing" by Lucas, Sander, and Taalman – Tom Copeland Nov 20 '20 at 17:57
-
More on eversion of a sphere in "Turning a surface inside out" by Phillips and the webpage A History of Shere Eversion (http://torus.math.uiuc.edu/jms/Papers/isama/color/opt2.htm) – Tom Copeland May 06 '21 at 06:15
-
1
-
Great resource on math and art: https://www.bridgesmathart.org/ and http://gallery.bridgesmathart.org/exhibitions – Tom Copeland Oct 15 '21 at 19:02
-
Don't we generally stick to one example per answer on these big-list questions? – Gerry Myerson Sep 23 '22 at 10:52
-
Gerry, is this the regal 'we', the OCD cadre 'we', or for some incomprehensibly strange reason do you somehow believe I belong to some group of yours? If you want to enlist your cohorts for some cause, surely you know meta is the preferred venue. – Tom Copeland Sep 23 '22 at 14:56
-
"We" refers to the users who have spent enough time on MathOverflow to have learned the customs of this website. "We" also know that if you want to ensure that I see a comment intended for me, you have to put @Gerry in it. – Gerry Myerson Sep 26 '22 at 12:57
-
More on Seifert surfaces: Surfaces So Different Even a Fourth Dimension Can’t Make Them the Same by Hartnett (https://www.quantamagazine.org/special-surfaces-remain-distinct-in-four-dimensions-20220616/). – Tom Copeland Oct 11 '22 at 23:24
-
3-D print your own polytopes: https://veraviana.net/history-of-polyhedra/danielebarbaro/ – Tom Copeland Mar 27 '24 at 08:30
Adding to the list two of my favorite mathematical sculptors:
George Hart:
http://www.georgehart.com/sculpture/sculpture.html
Bathsheba:
Finally, there are a lot of nice things at the new Geometry Playground in the Exploratorium, for anyone coming through the SF bay area:
- 7,755
-
Comments about and samples of George Hart's fascinating work can be found here:
http://richbugger.wordpress.com/2009/12/04/brilliant-geometric-sculptures-from-george-hart/
– Joseph Malkevitch Jul 20 '10 at 01:09 -
+1 for George Hart; I had the pleasure of taking a few of his classes at Stony Brook. He's a great teacher, and a great person. Also, mathematical sculptures are his life. – BlueRaja Jul 20 '10 at 06:04
A month ago our team completed, over four days, a very large geometric sculpture out of 20 tons of snow. Eva Hild of Sweden designed it and came over to work with us. The complete story is at
http://stanwagon.com/snow/breck2011/index.html
The videos linked at the top of the page allow you to walk around the work.
Eva Hild, her model, and our completed work. A view at night, showing the effects of the new LED lighting system.
Stan Wagon
- 2,542
- 151
-
Wow! Very impressive. Shame that it will probably be left to melt (although the evolution of that might also be cool). – Todd Trimble Feb 08 '14 at 12:47
at Ohio State ...
The Garden of Constants is a sculptural garden of large numerals that highlight the activities performed in nearby College of Engineering buildings. The installation, by Barbara Grygutis, includes a black walkway featuring 50 individual formulas cast in bronze and embedded in handmade pavers. The Garden of Constants is on the lawn of Dreese Laboratories.
- 40,238
-
-
1Victor, there are other numbers there besides 1 and primes, actually. They're just out of view. – KConrad Jul 20 '10 at 04:50
-
4
-
-
24
-
2I see now that the $8$ can also be read as $\infty$, which would answer the "largest number" question of @DouglasS.Stones :-) – Noam D. Elkies Dec 16 '18 at 15:52
Borromean rings on campus of George Washington University in Washington, DC. 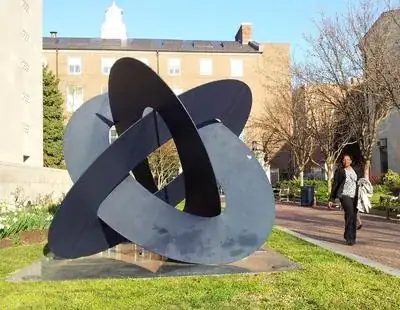 Unfortunately, I didn't make a note of the name of the artist.
Unfortunately, I didn't make a note of the name of the artist.
- 39,024
-
2
-
@KCo, I'll try to find it on my computer. Meanwhile, I found a pictur of it on the web. – Gerry Myerson Dec 16 '18 at 08:33
I suspect that the Octacube is also the only mathematical sculpture (possibly the only mathematical topic?) to appear in the journal Playboy (March 2006).
- 1
- 2
I think tensegrity sculptures are cool. Kenneth Snelson does a lot of these.

(source: well.com)
- 2,743
- 22,599
Cliff Stoll makes Klein bottles and sells them too. He's made the "worlds biggest klein bottle". You can see that here.
- 39,024
- 829
Alessandro Giorgi has made a bunch of statues concerned with the mathematics of juggling, e.g. 1 and 2.
- 19,330
- 27,645
-
It seems a bit misleading to have the balls attached to circles. Real juggling balls follow parabolic trajectories...! – Tobias Fritz Nov 15 '13 at 14:50
A ruled surface seen at the Peggy Guggenheim collection in Venice (I believe it is by Antoine Pevsner):

- 5,064
-
That's really nice. Do you happen to know the medium it's done in? I think my mother (who is a sculptor) would be intrigued. – Todd Trimble Feb 08 '14 at 12:45
-
@ToddTrimble: Hi Todd, it had a "coppery" look, but not sure if it was mixed with anything else. – pinaki Feb 19 '14 at 13:50
Here are some sculptures by Henry Segerman: https://plus.google.com/u/0/photos/102006004474081559466/albums/5946201022131183089
- 239
Among several of his sculptures, personally for me the neatest one -

(it's at the Newton Institute)
- 17,468
The sculptures of Morton C Bradley are not so widely known. He was originally an art conservator in Boston, but he also explored geometric shapes and color to create many sculptures. They are "a reflection of his fascination with the science of color, his admiration for traditional patterns, his exploration of mathematical designs." (Quote from web site below.) He never sold a single piece of work. At his death he donated his entire estate to Indiana University. The IU Art Museum is cataloging his work and arranging exhibits. They've created a web site http://www.iub.edu/~iuam/online_modules/bradley/ that discusses and displays some of his work. In comparison with other work already mentioned here, perhaps the most significant thing is his deep exploration of color in his sculptures.
- 3,226
I am by coincidence in Paris at this moment, attending a meeting (the first) of ESMA, the European Society for Math and Art. George Hart is giving a talk in two hours on his sculpture. The website of ESMA is here: http://mathart.eu/ and the program of the meeting here: http://mathart.eu/en/conf10program.html, and a web tour of the associated exhibition is here: http://mathart.eu/ihp10/index.html There was a talk yesterday about Stan Wagon's snow sculptures by John Sullivan, one of the team.
- 15,150
Stan Wagon (with various collaborators) is known to make snow sculptures that are mathematically pleasant.
- 9,666
- 6
- 54
- 83
I like the 4 dimensional mathematical sculptures by Bathsheba Grossman, such as the 24-cell:
http://www.bathsheba.com/math/24cell/24cell_new_th.jpg
Are the cryptographic sculptures by Jim Sanborn -- Cyrillic Projector, etc. -- close enough to a "mathematical sculpture"?
- 101
The MSRIs eightfold way
- 4,309
-
2
-
-
1Although the picture in the post no longer works, I suppose that some photos can be found elsewhere. – Martin Sleziak Jul 14 '19 at 12:46
Does the National Aquatics Centre in Beijing count? It illustrates the Weaire-Phelan structure, a recent (and the first) counterexample to Kelvin's conjecture.
Here's one of a large number of nice mathematical sculptures at the Science Museum in London.
This sculpture is made of 30 interlocking pieces and requires many hands to assemble or disassemble.
This sprinkler illustrates a theorem that a 3d solid can be constructed to cast any desired set of silhouettes (also illustrated on the cover of Gödel, Escher, Bach).
The last three were found on the three-dimensional geometry page of this wonderful collection.
Finally, a shameless plug of one of my own questions.
- 3,512
The Found Math galleries at the MAA website include many mathematical sculptures.
- 39,024
Check these out...they spring into shape by creating parallel folds on an initial paper shape:
http://erikdemaine.org/curved/
Erik Demaine is a mathematician (computational geometer) at MIT.
- 6,987
- 6
- 68
- 110
-
4One cannot mention Erik Demaine without also noting Robert Lang. http://www.langorigami.com/ – Willie Wong Jul 19 '10 at 13:00
-
Most of the artistic work of the Italian Attilio Pierelli was inspired by mathematics and notably by the idea of representing the fourth dimension. You can see some pictures of his "hyperspaces" at his site: www.pierelli.it/

- 25,490
- 3,347
- 18
- 24
The french sculptor Bernar (sic) Venet: see http://images.math.cnrs.fr/Bernar-Venet-de-l-art-et-des.html
- 37,143
- 3
- 82
- 142
-
-
I liked how the devotee of art was staring at "S Matrix Element, 2001". – Todd Trimble Feb 08 '14 at 12:42
The gömböc—as, for example, in this image—is a homogeneous convex solid with one stable, one unstable, and no neutral point of equilibrium on a horizontal plane. Its existence was conjectured by Vladimir Arnol'd in 1995 proved in 2006 by Gábor Domokos and Péter Várkonyi. Its manufacture requires great precision, and true gömböcs are not hand-made by individual artists.
- 6,001
- 2,427
-
(Just checking: did you intend to write that true gömböcök are not hand-made by artists? It kind-of makes sense, though the opposite statement would also make sense, so this could be an oversight. I shy away from changing this, of course, and will only correct the spelling.) – Peter Heinig Mar 05 '18 at 08:34
-
1@PeterHeinig: (1) In English, it is normal to anglicize the spelling, pronunciation, and grammatical declension of foreign words. My preferred spellings of gomboc and its plural form gombocs were both edited to gömböc; but in your comment the plural is distinguished as gömböcök. (2) The manufacturing tolerance is one part per thousand over a convex shape defined by complicated mathematical formulas. So the gomboc is well suited to computer-guided machining and would be very difficult, if possible at all, for a human sculptor to make. – John Bentin Mar 05 '18 at 10:12
-
Thanks. I am sorry, the missing 's' after the second 'gömböc' was simply my mistake. I'll correct it. The umlaut seems very usual even in the English literature on the subject, though, so I'll keep the umlaut. Thanks for clarifying that gömböcök are usually not manufactured by individuals. – Peter Heinig Mar 05 '18 at 10:39
-
Here's a link https://en.wikipedia.org/wiki/File:G%C3%B6mb%C3%B6c_statue.jpg to a large sculpture in Budapest that you could include in your post and a nice paper "Geometry and self-righting of turtles" by Domokos and Varkonyit (http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.528.7353&rep=rep1&type=pdf) – Tom Copeland Sep 24 '20 at 19:04
There are a few lying around Fine Hall in Princeton. One I think is "Five Disks: One Empty" by Alexander Calder.
There's also Marc Pelletier's "Polydodecahedron" which was gifted to JH Conway. http://www.princetonoccasion.org/quarkpark/pages_statements/Conway.html
There's also this big Obelisk in the common room (or did it get moved recently? I seem to remember its relocation when they redid the flooring). I had forgotten what it is actually called and what mathematics it is supposed to represent. Someone should edit this to add in the details.
- 37,551
"Tucker's group of genus 2" by Duane Martinez and DeWitt Godfrey
http://www.colgate.edu/news/blog/archives/archivedisplay?nwID=5031
http://commons.wikimedia.org/wiki/File:Tucker%27s_Genus_Two_Group.jpg
- 915
-
The Colgate image, and the Wikipedia article and image, have all been deleted. However I kept an image of part of the sculpture (a detail of a photograph, though it looks like a computer-generated image) at http://www.weddslist.com/groups/genus/g2/sculpture.jpg . The physical sculpture is in Slovenia, in this museum: http://www.burger.si/Bistra/BistraENG.html – maproom Nov 11 '13 at 16:53
Miguel Berrocal.
http://www.berrocal.net/index_eng.html
I also remember a beautiful article by Martin Gardner on the mathematical aspects of his sculpture.
- 56,550
- 4
- 116
- 260
George Green's windmill in Nottingham has a sculpture with a mill wheel with Green's Theorem carved into it.
- 9,052
-
Background: "George Green, Mathematician and Physicist 1793-1841" by Cannell and Lord (http://www.jstor.org/stable/3619259), and "From Grindstones to Theorems: The History of Green's Mill" by Ian Douglas (https://www.timetravel-britain.com/articles/museums/greensmill.shtml). – Tom Copeland Nov 09 '20 at 16:25
Credit to the photographer for this shot of Charles O. Perry's 'Solstice' in my downtown Tampa (a '2/3-twist triangular torus Mobius strip' according to him in this article about his work)
- 429
Sugimoto Hiroshi has made some beautiful mathematical surfaces. They are described in his book Conceptual Forms and also in his web site. I have seen some of them "live" in the museum island of Naoshima.
- 32,811
Jane and John Kostick make many mathematically inspired sculptures some of which can be seen here: http://www.jjkostick.com/jjkostick/Welcome.html
For example, Jane made a coffee table whose base is a trefoil knot.
For two more examples of sculptures that Jane built, please see the December 2008 issue of the Girls' Angle Bulletin, which can be downloaded from: http://www.girlsangle.org/page/bulletin.html
- 870
Frank Stella's Alu Truss Star (gallery website) is currently in the sculpture garden of the New Orleans Museum of Art. I believe it's a stellated dodecahedron, about 14 feet tall. I spent a few minutes looking at it from different angles to observe its symmetry when I ran across it in situ.
- 40,238
- 13,858
I think there are some sculptures by Helaman Ferguson on the campuses of Macalester College and the University of St. Thomas, both in St. Paul, Minnesota.
- 11,922
- 11
- 81
- 119
Perhaps these are too small to count as sculptures, but there is quite a respectable collection of models of mathematical objects on display in the Mathematical Institute in Goettingen.
- 4,678
Hyperboloids! Not necessarily a famous sculpture but very nice to look at. I have seen them everywhere from math classrooms to gardens!!
- 173
Kryptos, Jim Sanborn, Langley Virginia USA
https://www.wired.com/2013/07/nsa-cracked-kryptos-before-cia/
- 1
Sculpture by Nina Douglas, at the Simons Center for Geometry & Physics
(There is also a copy at IHES)
- 875





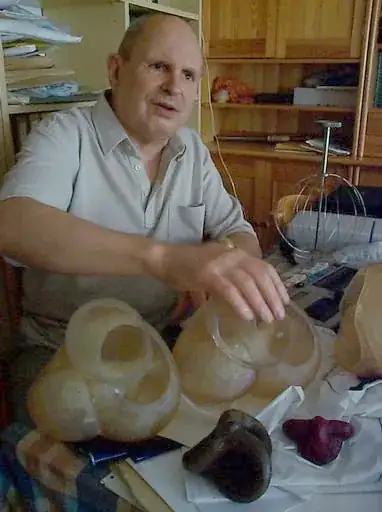

![Max Bill, 'Tripartite unit' [Unidade Tripartida]](../../images/1a8eb616b8fca718d3771869ea97820c.webp)















