10

This is more of a curiosity to me, but I'm sure I don't have the mathematical skills to answer it. That said... I took a look at several other posts with questions that relate to this one, but I haven't seen this specifically addressed...

Given a uniform solid rhombicosidodecahedron, what are the odds of rolling each of the faces: triangle, square and pentagon?

I'm interested in a theoretical answer here, I'm not concerned with reality... like a roller trying to "cheat" the roll for a specific outcome. And I'm obviously not concerned with the die being "fair". So let's assume that the roll is truly random.

TwoScoopsOfHot
  • 103
  • 4
    related: https://mathoverflow.net/questions/46684/fair-but-irregular-polyhedral-dice – Carlo Beenakker Apr 26 '18 at 21:04
  • 2
    This can be calculated by finding the solid angles, e.g. with the tetrahedral formulas at https://en.wikipedia.org/wiki/Solid_angle#Tetrahedron, using the Cartesian coordinates in the article linked in the question. –  Apr 26 '18 at 21:22
  • 3
    I am doubtful that simple geometry will resolve this issue; here is an article from the physics literature that addresses some of the complicating factors. – Carlo Beenakker Apr 26 '18 at 21:57
  • The spherical approximation should do for “a theoretical answer” or for the limit of a die thrown high above an adhesive surface. –  Apr 27 '18 at 14:33
  • Not sure what you mean by "spherical approximation". But I'll take a stab at it.... If I take the orthographic projection and measure the surface area for each face type, the ratios there would give the answer? If so, would that not be the same as the ratio of their areas without the projection? – TwoScoopsOfHot Apr 27 '18 at 14:45
  • 2
    I agree with Carlo Beenakker; it is unclear what is meant by a "theoretical answer." As soon as you talk about "rolling," you must at minimum bring physics into the picture, and then lots of complicated considerations immediately arise. See for example this paper: https://www.researchgate.net/publication/234029725_The_three-dimensional_dynamics_of_the_die_throw – Timothy Chow Apr 27 '18 at 20:15
  • 3
    @MattF. : Your "spherical approximation" sounds like Simpson's model, which, as the paper cited by Carlo Beenakker explains in detail, is a poor fit to experimental data. It might be okay for an "adhesive surface" if by that you mean a surface that brings the die's motion to an abrupt halt the instant it first touches the surface, but this is not what most people think of as "rolling" a die. – Timothy Chow Apr 27 '18 at 23:38
  • "Theoretical answer", I'll try to explain. For example, on a 6-sided die (d6), the theoretical odds for each side are 1 in 6. That can be effected by people weighting the die, or rolling in a certain manner, or even by the die having some edges slightly scuffed, etc. I'm not concerned about any of those factors. So, if I had asked the question about a d6, I would be expcting the answer of 1 in 6 for each side. – TwoScoopsOfHot Apr 28 '18 at 14:42
  • @TimothyChow, it's a poor fit for an oblong solid, but this solid is close to spherical. –  Apr 29 '18 at 17:22
  • See Bill Thurston's musings in the posting to which Carlo linked. E.g., "If the projected image of a die along a certain axis is almost round, then at low energy levels it should roll more easily about those axes than about axes where the projection is bumpy, other things being equal. This suggests larger components of the phase space for these kinds of rolls, when the phase space becomes disconnected." – Joseph O'Rourke Apr 29 '18 at 17:30
  • Note circumradius/inradius = 1.05 for this solid (http://mathworld.wolfram.com/SmallRhombicosidodecahedron.html) vs 2.55 for the die in the linked arxiv article –  Apr 30 '18 at 23:16

1 Answers1

8

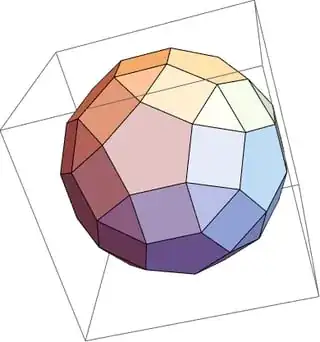
As a first pass, we can approximate the odds of landing on a face by projecting the polyhedron on a sphere, and taking the fraction of the sphere which it covers.

polyhedronprojection

Then the odds of a triangular, square or pentagonal roll overall are $$14.4\%,\ 50.4\%,\ 35.1\%$$ and the odds for an individual triangular, square or pentagonal face are $$0.72\%,\ 1.68\%,\ 2.93\%.$$

This is Simpson's method. It also represents the result of throwing the die high above an adhesive surface, so that the die is well-randomized in the air, and then after touching the surface falls onto the nearest side.

The angles have exact formulas which are easy enough to calculate in Mathematica:

data = PolyhedronData["SmallRhombicosidodecahedron"];
faces = Map[data[[1, 1]][[#]] &, data[[1, 2, 1]]];
angle[a_, b_, c_] := 2 ArcTan[Abs[a.Cross[b, c]]/
     (Norm[a] Norm[b] Norm[c] + a.b Norm[c] + b.c Norm[a] + c.a Norm[b])];
Map[Length[#] angle[# // Mean // Simplify, #[[1]], #[[2]]] &, faces]
     // FullSimplify // Union

This gives the following solid angle measures for each triangular, square or pentagonal face: $$6 \cot^{-1}\left(2 \sqrt{3} u+\sqrt{124 u-61}\right),\\ 8 \cot^{-1}\left(2u+\sqrt{40 u-21}\right),\\ 10 \cot^{-1}\left(2 \sqrt{5u}+3 \sqrt{2u+1}\right)$$ where $u=5+2\sqrt{5}$.