10

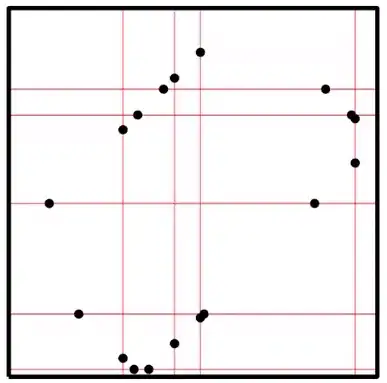
A while ago I saw an image like the one below in a lecture, which was supposed to represent a rail network in a (square) city:

Rail network in a city

The circles represent trains that are moving either North/South or East/West along the vertical and horizontal tracks. The purpose of this picture was to show that, even though the grid is unevenly spaced, it is always possible to schedule the trains so that connections were perfectly timed: that is, any time a train arrives at an intersection, there is another train also arriving at that intersection, in a perpendicular direction.

The math behind this is very simple, so my question is: what is the area of study in which one would encounter an image like this?

Tom Solberg
  • 3,929
  • 1
    It seems very likely that someone fluent in the theory of configuration spaces will be able to formalize this. Please note that I am not saying that the connection of this problem to configuration spaces is clear and canonical, but I think that 'configuration space' is the 'direction in knowledge space' in which you should go, possibly asking someone working in this direction. – Peter Heinig Sep 25 '17 at 11:46
  • For what's it's worth, let me remark that I think I have seen many mathematical pictures and mathematical exhibitions, have never seen this before, and find it a pleasure to see. I think that (copies of) this should be 'inducted' into, simultaneously, the Mathematikum, the MoMath, and the ix-quadrat. Seriously. – Peter Heinig Sep 25 '17 at 15:31
  • On a utopian note, this illustration could also be something of an 'interface' between a traditional 'modern art' museum, and a 'mathematics museum', perhaps both existing in 'cyberspace'. I mean that without the moving points, this could be an 'exhibit' on the 'wall' of the 'modern art museum', and then there could be a 'button' saying 'enter the mathematics museum', upon the pressing of which the points appear and one moves through the 'canvas' into the 'mathematics museum'. And vice versa (perhaps). – Peter Heinig Sep 25 '17 at 15:37
  • 3
    Not an answer, but isn't the creation of such a situation trivial? Place horizontal and vertical lines randomly in $[0, 1] \times [0,1]$ and place "trains" on the lines at positions $(a_i, a_i)$ and set them running with constant speed. – David G. Stork Sep 25 '17 at 16:34
  • @David, yes, absolutely so. The result was a little surprising to me at the time so I hoped this was part of some wider branch of literature. PS love your book – Tom Solberg Sep 25 '17 at 18:00
  • @TomSolberg. Perhaps you've seen my generalization of your problem (https://mathoverflow.net/questions/281987/train-intersection-problem-with-unequal-speeds). And thanks for your kind words... I'm working on the third edition in the CDF interactive format (http://www.wolfram.com/cdf/). It will blow your mind (if I do say so myself). – David G. Stork Sep 25 '17 at 18:12
  • @DavidG.Stork Frankly I don't see your solution. It guarantees that any two trains always pass at their starting position, but how does it guarantee that each of the trains meets another train at the other intersections it passes? Also note that in the picture the NS trains have 5/4 as many rendezvous as the EW trains, so multiple rendezvous are needed. Sorry to be dense. – Brendan McKay Sep 26 '17 at 04:52
  • 2
    @Brendan, his solution is actually exactly what's being shown in my picture. Notice that the cars all hit the diagonal of the square at the same time. – Tom Solberg Sep 26 '17 at 12:34
  • 2
    @BrendanMcKay: Consider: a train at $(x_1, x_1)$ will meet a train at $(x_2,x_2)$ at point $(x_1, x_2)$ after both have traveled the same distance, $d = |x_1 - x_2|$, at the same speed... and hence at the same time. True for all pairs of trains. – David G. Stork Sep 26 '17 at 16:16

1 Answers1

4

Not an answer, but two related, almost inverse topics suggesting in which areas of mathematics they fall:

(1) The Lonely Runners Conjecture. See, e.g., Terry Tao, "Some remarks on the lonely runner conjecture." Perhaps this could be classified as a mixture of number theory and combinatorics.

Lonely
Guillem Perarnau, Oriol Serra, "Correlation Among Runners and Some Results on the Lonely Runner Conjecture." Electr. J. Comb. 2016.

(2) "At Museum of Mathematics, Meet 2 Beavers That’ll Never Meet." This construction uses Truchet Tiling. Perhaps this could be classified as a mixture of topology and combinatorics.

Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933