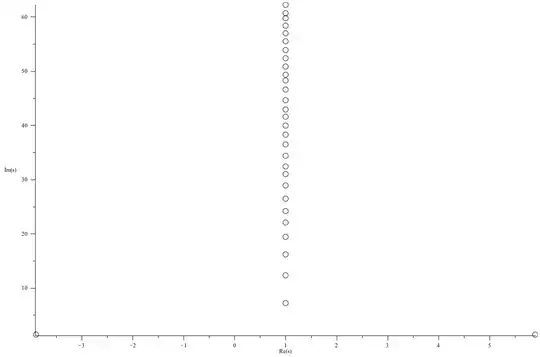
Or stated differently: for $s \in \mathbb{C}$ and with $\chi(s)= \pi^{-s}\,2^{1-s}\,\cos\left(\frac{\pi\,s} {2}\right)\,\Gamma(s)$, do all, except a finite few, of the complex (real ones exist as well) zeros of:
$$\frac{\zeta(s-1)}{\zeta(s)}-\frac{\pm 1-\chi(s)}{\pm 1-\chi(s-1)}$$
reside on the line $\Re(s)=1$ ?
The finite few lying off the line are:
- $\pm = +$ the exceptional set: $(5.894... \pm 1.389...\,i)$ , $(2- 5.894... \pm 1.389...\,i)$
- $\pm = -$ the exceptional set: $(3.006... \pm 2.438...\,i)$ , $(2- 3.006... \pm 2.438...\,i)$
Could a proof for this be within reach or is it just as hard as the RH?
Thanks!
Added a graph of the + version on request.