12

For $k \ge 1$, let $f_d(k)$ be the largest possible number of points $p_i$ in $\mathbb{R}^d$ that determine at most $k$ distinct (Euclidean) distances, $\|p_i-p_j\|$.

Example. For points in the plane $\mathbb{R}^2$, $f_2(1)=3$ via an equilateral triangle, and $f_2(2)=5$ via the regular pentagon.

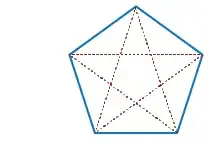
RegPentagon
It is clear that $f_d(k)$ is finite: it is not possible to "pack" an infinite number of points into $\mathbb{R}^d$ while only determining a finite number of point-to-point distances.

Q. What is the growth rate of a reasonable upper bound for $f_d(k)$?

I am particularly interested in $\mathbb{R}^3$. $f_3(1)=4$ via the regular simplex. I am not even certain what is $f_3(2)$. Does anyone know? Certainly $f_3(2) \ge 6$ just by placing one point immediately above the centroid of the pentagon.

But regardless of exact values, I would be interested in an upper bound for $f_3(k)$. As well as pointers to results in the literature. This question has an Erdős-like flavor, and undoubtedly has been considered previously. Thanks!

GH from MO
  • 98,751
Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933
  • 1
    Is this not a very well-known problem?: http://en.wikipedia.org/wiki/Erd%C5%91s_distinct_distances_problem – Sam Hopkins May 24 '15 at 01:41
  • 3
    It is related, but not exactly the same. In Joseph's version, k (number of distinct distances) is fixed and n is wanted, whereas the literature you mention seems to me to have n fixed and estimates k given n and d. However, that entry a good place to start. Also, the book titled something like "Unsolved problems in geometry" might have a discrete portion that gets closer to Joseph's question. Gerhard "Looking From The Other End" Paseman, 2015.05.23 – Gerhard Paseman May 24 '15 at 01:54
  • @SamHopkins: Yes, I think Gerhard's comment clarifies. The Erdős conjecture is that the min # of distances is $g_d(n)=\Theta(2^{n/d})$, which reverses to saying that my $f_d(k)$ grows like $d \log k$. This is already useful (Thanks!) but doesn't help me determine, e.g., $f_3(2)$... – Joseph O'Rourke May 24 '15 at 02:01
  • 1
    Don't know if this helps, but the octahedron is another example showing $f_3(2) \geq 6$. – Will Brian May 24 '15 at 03:23
  • 2
    Also, $f_d(k) < R(d+2,\dots,d+2)$ (where $R$ denotes the Ramsey number and there are $k$ entries). This is because you cannot have $d+2$ points that are all mutually the same distance from each other. Suppose you had $R(d+2,\dots,d+2)$ or more points and only $k$ distances represented. Think of these points as the vertices of a complete graph, and think of the distance between two points as the "color" of their edge. The definition of $R$ tells you that you have $d+2$ points all the same distance apart, a contradiction. Thus, for example, $f_3(2)$ is less than $R(5,5) \leq 49$. – Will Brian May 24 '15 at 03:46
  • 2
    Doesn't the pentagon give you $f_3(2)\ge 7$ if you add a point below also? – Anthony Quas May 24 '15 at 04:51
  • 1
    @Anthony is right. It so happens that the two extra points are distance $s$ from each other and from each of the pentagon points where the pentagon has side $s$. – Aaron Meyerowitz May 24 '15 at 07:22
  • @AaronMeyerowitz: Hmm. For a pentagon inscribed in a unit-radius circle, I find $s \approx 1.176$ while the distance from each added above/below point to a pentagon point is $s' \approx 1.160$. – Joseph O'Rourke May 24 '15 at 13:44
  • If Aaron is right, that would make the face angle of a regular tetrahedron exactly 72 degrees. Which it isn't. – The Masked Avenger May 24 '15 at 15:44
  • @JosephO'Rourke: Have you looked into the many recent techniques and approaches developed to attack the asymptotics of this problem? For instance it is still probably worthwhile to convert this to an incidence question. – Sam Hopkins May 24 '15 at 15:50
  • @SamHopkins: You are right, I need to study the Guth-Katz bound. – Joseph O'Rourke May 24 '15 at 15:53
  • 1
    Of course I was wrong. – Aaron Meyerowitz May 25 '15 at 07:18

2 Answers2

9

Bannai, Bannai and Stanton proved that $f_d(k) \leq {d + k \choose k}$ in 1983. See: http://link.springer.com/article/10.1007%2FBF02579288

I don't think this bound has been improved in general. It is certainly not tight for every value of the parameters.

The first good bound for this function was for $k = 2$, as given by Larman Rogers and Seidel in 1977, "On Two-Distance Sets in Euclidean Space". They proved that $f_d(2) \leq (d+1)(d+4)/2$ using a nice dimension argument. This bound was later improved by Blokhuis in 1981 to $(d+1)(d+2)/2 = {d+2 \choose 2}$, which was later generalised to $f_d(k) = {d+k \choose k}$.

This problem is also discussed in the manuscript "Linear Algebra Methods in Combinatorics" by Babai and Frankl, where you can find some of these proofs.

Anurag
  • 1,157
  • You are welcome. You can also find the proof of Larman, Rogers and Seidel here: http://mathoverflow.net/questions/17006/linear-algebra-proofs-in-combinatorics/206679#206679 – Anurag May 24 '15 at 16:34
2

In Graham's handbook of combinatorics volume one, chapter 17, Extremal problems in combinatorial geometry by Erdos and Purdy, section 5.3.1 has some upper bounds. It cites a paper showing $f_3(2)$ is 6 and it has some upper bounds for $f_d(2)$ and an upper bound for $f_d(k)$.

Kristal Cantwell
  • 6,433