Examples of Mathematical Beauty in School Mathematics

Question

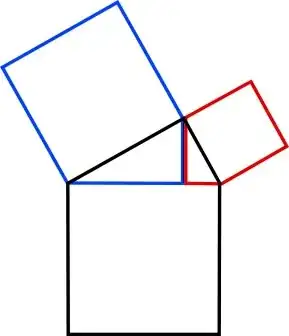
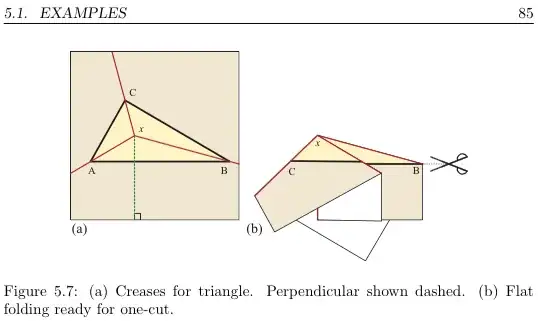
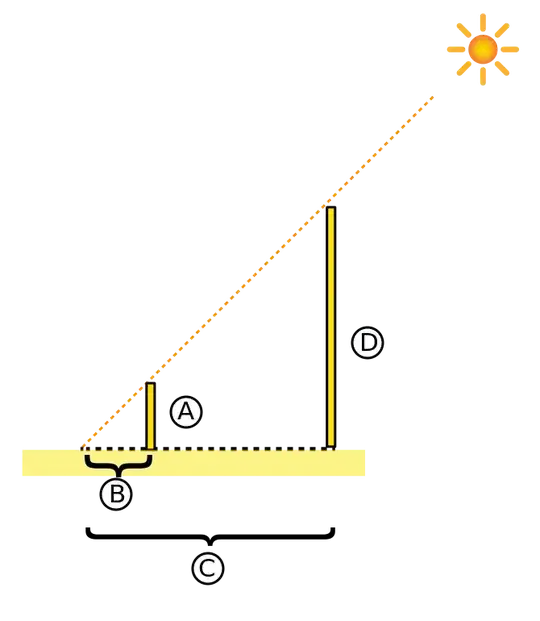
Various branches of mathematics have mathematical beauty. Some of this are visual, such as the mandelbrot set, while others are logically sublime, such as the recursive simplicities of peano arithmetic and surreal numbers. What are some examples of mathematical beauty in school mathematics. I am mostly intrested in any examples for High School, but any other K12 examples would be appreciated as well.

Also, I am not asking for things marginally related to a school subject, but something that either helps a student understand or reinforce an existing understanding of a mathematical concept by making it aesthetically pleasing.

This question is perhaps too broad for specific answers...? You might in the meanwhile peruse the responses to *Wonder as Motivation*, which displays some wonderful examples. — Joseph O'Rourke, Apr 11 '15 at 01:53
@JosephO'Rourke I am fine with answers specific to different subjects. No one answer has to be a catch-all. — Christopher King, Apr 11 '15 at 01:55
Perhaps you should expand on the phrase "school mathematics." — Joseph O'Rourke, Apr 11 '15 at 02:10
I voted to close even post-edit; I think tagging it algebra geometry trigonometry and asking for examples of "mathematical beauty" from anywhere in K12 is still too broad. If anyone (@JosephO'Rourke?) feels like generating an example, though, I think it would be interesting to consider the 1-1 correspondence between lines $y = mx + b$ and an $mb$-plane; so, e.g., each of the former lines corresponds to a unique point in the latter plane. What does an $mb$-line (or other figure) correspond to in $xy$? Similarly, take $y = x^2 + px + q$ and various correspondences with the $pq$-plane... — Benjamin Dickman, Apr 11 '15 at 04:16
I think this question is too difficult to answer because there is no clear definition of "mathematical beauty". Even "aesthetically pleasing" is difficult to find consensus on. — DavidButlerUofA, Apr 11 '15 at 18:17
See http://www.ams.org/notices/201103/rtx110300368p.pdf for some examples — Marius Kempe, Apr 12 '15 at 20:58

score 7 · Answer 1 · edited Apr 13 '17 at 12:19

7

Proofs of the Pythagorean theorem can be beautiful. #9 at cut-the-knot is my favorite (http://www.cut-the-knot.org/pythagoras/). Although this one on math stack exchange has its own beauty (https://math.stackexchange.com/posts/259966/revisions).

A visual proof of pythagoras theorem

edited Apr 13 '17 at 12:19

Community

1

answered Apr 11 '15 at 14:47

Sue VanHattum

20,344
2
42
99

(Thanks for adding the diagram for me.) – Sue VanHattum Apr 11 '15 at 20:24
Its a nice proof. I can actually remember it in its entirety, not just how to do it. – Christopher King Apr 11 '15 at 23:07
I actually blogged about all this, but blogger threw out my diagrams. Some day I'll have time to fix it. http://mathmamawrites.blogspot.com/2012/10/proving-pythagorean-theorem.html#comment-form – Sue VanHattum Apr 12 '15 at 16:48

score 5 · Answer 2 · answered Apr 12 '15 at 01:01

Mathematical beauty is in the eye of the beholder, so I hesitate to respond to this question just before it gets closed. But I'll share one example that I find aesthetically pleasing.

Suppose you desire to cut out a triangle from the middle of a piece of paper, not by punching the scissors through and cutting the perimeter, but rather by folding the paper and then cutting straight through the folded paper.

The natural solution is to mountain-crease (red below) the angle bisectors, and valley-crease (green dashed) a "perpendicular" from the incenter $x$:

^{(Figure from How To Fold It: The Mathematics of Linkages, Origami, and Polyhedra.)}

What I find so pleasing is that when you perform this physically, the angle bisectors meet at a point $x$ (the incenter), and one grasps Proposition 4, Book IV of Euclid viscerally. Naively, it could well be that the bisectors do not meet at a point. But careful creasing shows experimentally that they do.

I have found this tactile demonstration more convincing to (U.S.) 8th-graders than a two-column Euclidean proof.

Good answer, but one of the things I think is sort of sad is that demonstrations with specific triangles using non idealized paper is more convincing than a proof that it works for all triangles. Sigh. — Christopher King, Apr 12 '15 at 01:11
Can this be (injudiciously) extrapolated to find that visual (the example you given, tons of other here: http://math.stackexchange.com/questions/733754/visually-stunning-math-concepts-which-are-easy-to-explain? ) / physical (physics analogue, for example kinematics analogy of calculus) demonstration are lot more interesting than clunky Euclidean proof ? — , May 10 '16 at 16:45

score 3 · Answer 3 · answered Apr 11 '15 at 05:39

One reason motivated me to study math, was my bad math teacher from high school. She showed me too much math, but never showed what I can do with it.

I think you can make something as simple as the Thales theorem a relevant thing for them by showing a real application of it; instead of just focusing on shiny fractals or complex infinitesimal recurrences; that under the wrong circumstances will give the students the same feeling I had at high-school -yes, cool but useless. (my two cents).

high school theory

enter image description here

Real Life Application

Ballistics, positioning and triangulation of objects in a real or simulated setting (yes, video games!). This mixed with some basic physics v = d/t can bring some nice visualizations and predictions of that torpedo will hit the other ship.

enter image description here

score 2 · Answer 4 · answered Apr 20 '15 at 15:20

A fundamental topic in school mathematics is the notation of area. A remarkable result that can be treated at different grade levels is the nifty theorem known as the Bolyai-Gerwien-Wallace Theorem.

http://en.wikipedia.org/wiki/Wallace%E2%80%93Bolyai%E2%80%93Gerwien_theorem

Intuitively, the result says that two plane polygons have the same area if and only if it is possible to cut one of the polygons up into a finite number of polygonal pieces and reassemble these pieces to form the other polygon.

This property is sometimes called equidecomposability. There are still open questions about the minimum number of pieces for getting from one shape of polygon to another shape of polygon.

It is remarkable that the analog of this for 3-space is false. Hilbert's Third Problem asked whether a regular tetrahedron and cube of the same volume were "equidecomposable." Max Dehn showed that the answer was "no."

Examples of Mathematical Beauty in School Mathematics

4 Answers4