What theorems from single-variable calculus break down in the multi-variable context?"

Question

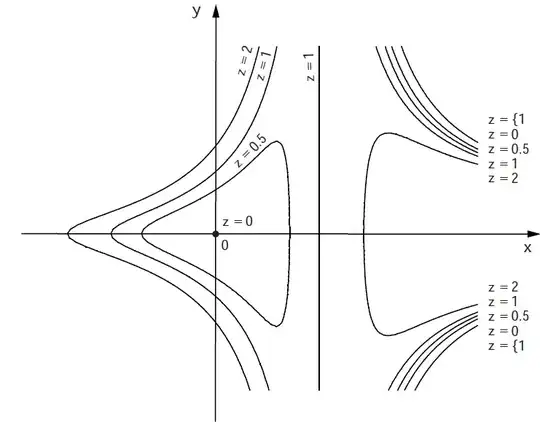
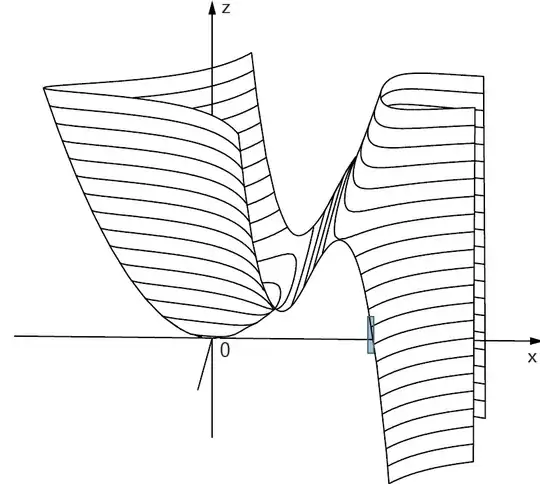
In teaching multi-variable calculus, it's insightful to discuss with students not only how certain concepts from single-variable calculus extend to multiple variables but also where these extensions fail. For example, while in single-variable calculus, a continuously differentiable function defined on an open interval that has a unique critical point, which is a local minimum, also has a global minimum at that point. However, this is not necessarily the case in multi-variable calculus, as there are known counterexamples. here is one for a two-variable function:

$z= f(x, y) = x^2 + (1 − x)^3y^2$ for this function, $(0, 0)$ is the single critical point that is a local minimum but it is not global

I am compiling a list of such instances to enhance my curriculum. Could you share other specific results or theorems that hold in single-variable calculus but do not necessarily apply in the multi-variable setting? Examples where the multi-variable context introduces significant complexity or entirely new phenomena would be particularly valuable.

Answer 1

Path-dependency of limits can lead to very counterintuitive results. For instance, consider the following limit:

\begin{align*}\lim\limits_{(x,y) \to (0,0)} \frac{x^2y}{x^4+y^2}\end{align*}

An intuitive-but-incorrect way to think about this limit is to imagine it only has one variable:

\begin{align*}\lim\limits_{x \to 0} \frac{x^2x}{x^4+x^2} = \lim\limits_{x \to 0} \frac{x}{x^2+1} = \frac{0}{1} = 0\end{align*}

The problem is that in the computation above, we evaluated the limit along the path $y=x,$ but this is just one of many possible paths.

Okay, then why don't we evaluate the limit along all lines through the origin? We can handle that in three cases: the general case $y=mx$ where $m$ is a nonzero constant, and then the cases $y=0$ and $x=0$ separately. The limit comes out to $0$ in all these cases:

\begin{align*}\lim\limits_{x \to 0} \frac{x^2(mx)}{x^4+(mx)^2} = \lim\limits_{x \to 0} \frac{mx}{x^2+m^2} = \frac{0}{m^2} = 0,\end{align*}

\begin{align*}\lim\limits_{x \to 0} \frac{x^2(0)}{x^4+0^2} = 0, \quad \quad \lim\limits_{y \to 0} \frac{(0^2)y}{0^4+y^2} = 0. \end{align*}

However, this is still not correct! Look what happens if you approach along the path $y=x^2.$ We get a different result:

\begin{align*}\lim\limits_{x \to 0} \frac{x^2(x^2)}{x^4+(x^2)^2} = \lim\limits_{x \to 0} \frac{x^4}{x^4+x^4} = \frac{x^2}{2x^4} = \dfrac{1}{2}\end{align*}

It turns out our limit $\lim\limits_{(x,y) \to (0,0)} \frac{x^2y}{x^4+y^2}$ evaluates to $0$ along all linear paths, but not along all paths in general (for instance, it came out to $\frac{1}{2}$ along a quadratic path). So generally speaking, our limit does not exist.

This is super weird and counterintuitive, but it's true, and you can get a better sense of why it happens if you look at the graph of $f(x,y) = \frac{x^2y}{x^4+y^2}{:}$

Answer 2

Critical points of smooth functions in one-dimension tend to be local extrema. This is because $f''(c)=0$ is an unlikely event. When $f'(c)=0$, we expect a local min or max, depending on the sign of the second derivative.

In higher dimensions, the critical points correspond to the simultaneous vanishing of all the first-partial derivatives. The second derivative becomes a matrix of second partial derivatives called the Hessian. For a critical point to be a local maximum or minimum, the eigenvalues of this matrix all have to be the same sign.

Since there are $n$ eigenvalues, and each can be either positive or negative, we have $2^n$ types of critical point behavior. Only 2 of these are a max or a min. So we should expect roughly $\frac{1}{2^{n-1}}$ of all critical points to be local extrema, with the rest saddles. This is imprecise since we have not clarified what "picking a function at random" means, but it is a solid intuition.

Answer 3

Existence of antiderivatives.

Every continuous function $f: \mathbb{R} \to \mathbb{R}$ has an antiderivative.

On the other hand, a continuous vector field $f: \mathbb{R}^d \to \mathbb{R}^d$ for $d \ge 2$ need not be the gradient of a function $u: \mathbb{R}^d \to \mathbb{R}$, in general. If the vector field $f$ is continuously differentiable, then the existence of a differentiable function $u: \mathbb{R}^d \to \mathbb{R}$ that satisfies $\nabla u = f$ is equivalent to the Jacobi matrix of $f$ being symmetric.

Another obstacle to the existence of such a $u$ that occurs in dimension $d \ge 2$ is the existence of holes in the domain of the function: let $\Omega \subseteq \mathbb{R}^d$ be non-empty and open and let $f: \Omega \to \mathbb{R}^d \to \mathbb{R}^d$ be a continuously differentiable vector field whose Jacobi matrix is symmetric. If $\Omega$ is, for instance, simply connected, then $f$ is a gradient, but there are more general domains $\Omega$ where this is not always true.

Answer 4

The inverse function theorem on $\mathbb R$ is global: any differentiable function $f \colon \mathbb{R} \to \mathbb{R}$ satisfying $f'(x) \neq 0$ everywhere has to be one-to-one, and so it has a global inverse $f^{-1} \colon f(\mathbb{R}) \to \mathbb{R}$.

The inverse function theorem on $\mathbb{R}^n$ is only local: if $f \colon \mathbb{R}^n \to \mathbb{R}^n$ is $C^1$-regular and $Df(x)$ is invertible, then $f$ is invertible on some neighorhood of $x$.

One can appreciate the difference by looking at the example of $\exp \colon \mathbb{C} \to \mathbb{C}$, which is clearly not one-to-one (we have $\exp(0) = \exp(2\pi i)$) but its derivative is everywhere invertible.

Answer 5

One elementary property that fails already for functions of one variable with values in $\mathbb{R}^n$ is the chord-tangent property. For example, for the helix $$ h:t\mapsto (\sin t,\cos t, t),\quad t\in[0, 2\pi], $$ we have $h(2\pi)-h(0)=(0,0,2\pi)$, however at no point on $[0,2\pi]$ is $h'$ equal, or even parallel, to $(0,0,2\pi)$. Of course, we mostly care about the chord-tangent property because it gives the bound $|h(b)-h(a)|\leq |b-a|\max_{(a,b)}|h'|$, which still holds in higher dimensions.

Answer 6

What about the generalized Stokes' Theorem ? In some sense this is a story about how Calculus III with it's three dimensional-centric formulae fails to generalize that story for arbitrary vector fields in higher dimensions. Why? Because something beyond vector fields are needed to understand the generalization of the FTC for higher dimensions.

In particular, we must introduce differential forms in $\mathbb{R}^n$. The degrees of freedom in a differential $p$-form in $\mathbb{R}^n$ is $\frac{n!}{p!(n-p)!}$. We need that many scalar functions to define a $p$-form. It just happens that $p=2$ and $p=3$ forms in $\mathbb{R}^3$ are both in one-to-one correspondance with vector fields. No such luck in higher dimensions in general, only the $1$-forms and $(n-1)$-forms are in direct correspondance with vector fields. Otherwise, the other objects described by $p=2,\dots , (n-2)$-forms are new objects which are not just another take on vector fields.

These new objects are fluxes. Yet, these play the role vector fields did in lower dimensions. For example, in electromagnetism in four spatial dimensions you'd find a Faraday tensor formed by more magnetic components than electric components.In short, the FTC does not generalize for vector fields, it generalized for differential forms. It is a happy accident of low dimensions that we didn't need differential forms to understand the FTC. $$ \int_M d\alpha = \int_{\partial M} \alpha $$