Why are there two inverses to exponentiation?

Question

I'm not sure if this is more educational or more "pure math", but:

For multiplication and addition, there is exactly one inverse operation, namely division and subtraction.

For exponentiation, we have both logarithms and roots.

Why is that the case? Maybe one could argue that exponentiation is "even less commutative" than division and there is a difference in solving for x in $x/4=5$ and $4/x=5$, but that doesn't feel quite right to me...

Because addition and multiplication are commutative, while exponentiation is not. You are considering functions of two variables and asking for the inverse in one of those variables. When the function is symmetric in the two variables, the two inverses coincide. — Michael Bächtold, May 23 '23 at 12:27
@MichaelBächtold: I'd upvote that for brevity if you made it an answer. — Daniel R. Collins, May 23 '23 at 14:28
(+1) This might seem better suited for MSE than here, but I think this is a question that a teacher is likely to encounter in a school algebra class (or a college algebra class, or precalculus class), and also a question that some beginning teachers might not be able to adequately (or quickly enough) answer. Of course, the answers given thus far are probably written a bit too advanced for direct student consumption, but not for a teacher who I would expect to be able to translate to the level of the students they are dealing with, an assumption I think is appropriate for this group. — Dave L Renfro, May 23 '23 at 19:08
I don't think roots are an inverse of exponentiation. They are a form of (or extension of) exponentiation. Saying that roots are an inverse of exponentiation is kind of like saying multiplying by 0.1 is the inverse of multiplying by 10. — DKNguyen, May 24 '23 at 01:34
@DKNguyen There is nothing wrong or unusual about inverses being operations of the same type. For example, the inverse of a linear transformation is a linear transformation; the inverse of a rotation is a rotation. — Will Orrick, May 24 '23 at 11:41
@WillOrrick I guess I don't really consider the inverse matrix to be an inverse OPERATION. I consider the MATRIX to be inverted rather than the operation itself. — DKNguyen, May 24 '23 at 14:47
@DKNguyen: "... is kind of like saying multiplying by 0.1 is the inverse of multiplying by 10." -- Which it is. And I would say so any day. And regarding your last comment, well, the (1-by-1) matrix $0.1$ is the inverse of the (1-by-1) matrix $10$. — Torsten Schoeneberg, May 24 '23 at 14:50
@TorstenSchoeneberg The distinction I was trying to make is an inverse of the operator vs the inverse of the arguments or things being operated on. — DKNguyen, May 24 '23 at 14:51
@DKNguyen You don't really need to maintain a rigid distinction between inverses of elements and inverses of operators because one can freely move back and forth between elements and actions. In the multiplicative group of nonzero rational numbers the element 10 has an inverse, the element 0.1 There is an action of this group on the set of rational numbers by multiplication. The element 10 transforms the rational number $x$ into $10x$; the element $0.1$ transforms $x$ into $0.1x$. The inverse transformation of $x\mapsto10x$ is $x\mapsto0.1x$. (They undo each other.) — Will Orrick, May 24 '23 at 17:42
This is a great explanation of why the non-commutativity of exponentiation is crucial here. — J.G., May 24 '23 at 18:54

Justin Hancock · Accepted Answer · 2023-05-23T13:48:52.437

84

The concept of an inverse operation itself is a bit tricky. Often we consider arithmetic operations to be binary operations: $\DeclareMathOperator{\add}{add}$ $\DeclareMathOperator{\subtract}{subtract}$ $$\add(a,b)=a+b,$$ $$\subtract(a,b)=a-b.$$

This is the view we take when we make statements like “addition is commutative,” which is the same as saying $\add(a,b)=\add(b,a)$. However, in this view, addition and subtraction are not inverses of each other. Subtraction does not take the output of addition and return the inputs.

To make sense of the statement that subtraction is the inverse operation of addition, we need to view arithmetic operations as unary operations or single-variable functions: $$\add_a\!(x)=x+a,$$ $$\subtract_a\!(x)=x-a.$$ In this view, it’s true that $\add_a\!$ and $\subtract_a\!$ are inverses. They undo each other. This is why I prefer to tell students that “subtracting $a$ undoes adding $a$.”

However, there’s a problem. We’ve defined $\subtract_a\!(x)$ to mean “subtract $a$ from $x$.” But what about the operation “from $a$ subtract $x$?” From the binary-operation perspective, this is just $\subtract(a,x)$ instead of $\subtract(x,a)$. But from the unary-operation perspective, this is a completely different kind of operation: $$\operatorname{subtractfrom}_a\!(x)=a-x,$$ and it is actually it’s own inverse. Suppose we have a bottle of water that has volume $a$ and we spill an unknown volume $x$. How can we recover the information of how much we spilled? We can take the remaining volume and subtract it from the original volume, $a-(a-x)=x$.

This demonstrates that a non-commutative binary operation has two types of associated unary operations, and they have different inverses. The same is true for division. “Divide $x$ by $a$” and “divide $a$ by $x$” are different functions of $x$ with different inverses. The same is also true for exponentiation, and language for distinguishing the two kinds of functions already exists.

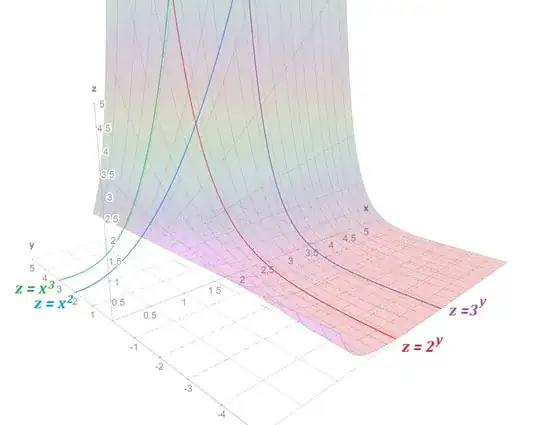
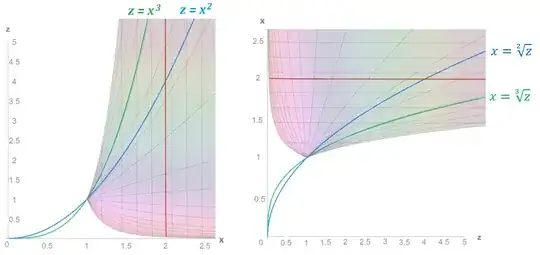
The functions $$\operatorname{power}_a\!(x)=x^a$$ are commonly known as power functions. Their inverses are other power functions, $(x^a)^{1/a}=x$. When $a$ is a positive integer, $x^{1/a}=\sqrt[a]{x}$ is also called a root function.

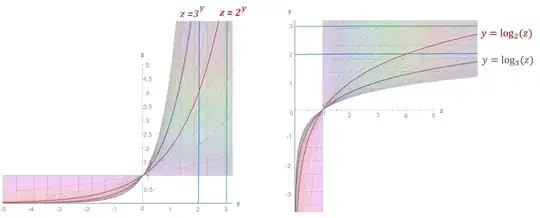
The functions $$\exp_a\!(x)=a^x$$ are commonly known as exponential functions. Their inverses are logarithmic functions, $\log_a\!(a^x)=x$.

I have to explain this frequently to students in single-variable calculus who are learning derivative rules. Power functions and exponential functions both involve exponentiation, but they are fundamentally different functions with different derivatives: $$\frac{\mathrm d}{\mathrm d x}x^a=ax^{a-1},$$ $$\frac{\mathrm d}{\mathrm d x}a^x=a^x\ln a.$$ The mnemonic I give them is that “$a^x\!$ is an exponential function because the variable is in the exponent.”

edited May 23 '23 at 13:48

answered May 23 '23 at 13:32

Justin Hancock

3,050
6
23

4

Beautiful, thorough, and educational answer! – Greg Martin May 24 '23 at 07:16
2

subtact_a(x) vs. subtractfrom_a(x) makes me think of ARM assembly language, which has both a sub instruction and a reverse-subtract instruction, so you can do sub r0, r1, #5 to do r0 = r1 - 5 or rsb r0, r1, #5 to do r0 = 5 - r1. (Where r0 and r1 are registers, and #5 is an immediate constant that becomes part of the machine code for the instruction). Fun fact: it makes sense that ARM has rsb but most ISAs don't, because ARM's final operand can also be a shifted-register, so it's not just immediates constant with asymmetry. "Free" shifts are one of ARM's fun features. – Peter Cordes May 24 '23 at 14:20
1

Good answer. Suggestion: The key part of the answer are the two paragraphs starting with "The functions", so I suggest moving that up to the top and placing the rest as further elaboration underneath. – May 25 '23 at 02:39
4

@user24096: Nah, the key part of the answer is the exploration of the relationship between binary operations and unary operations that fix one argument of the binary operation, and how that relates to the concept of an inverse. The section about power and exponential functions is about how those functions fit into the context established by the rest of the answer, and it needs to come after that context is established. – user2357112 May 25 '23 at 11:08
1

As a prof. math'n, I think we do a great disservice by teaching add/sub/mult/div are 4 diff. operations and that add & sub and mult & div are inverses. Not only are they non-invertible opns, but there are only 2 opns: add & mult. Add & sub (and mult & div) are the exact same opn. $0$ is the add identity bc for all $x$, you get $x$ back: $x+0=x$ (and $1$ is mult id. bc $x\cdot 1=x$). Then, $a$ has the add inverse $-a$ bc it takes you back to the add id.: $a+-a=0$ (and if $a\ne 0$ its mult inv. is $a^{-1}$ bc $aa^{-1}=1$). Now it's easy to see why you can't div by $0$. $0y=1$. $0^{-1}=y=$? – Travis Bemrose May 25 '23 at 20:09
1

@TravisBemrose: I think it's also important to recognize that "multiply something by an integer" and "multiply something by something of its own type" are different operations, as are "raise something to an integer power" and "raise something to an exponent of its own type". The first type of multiplication is actually defined in terms of addition, while the second is an operation of its own. Likewise, the first kindof exponentiation is defined in terms of multiplication, but the second one isn't. Some kinds of algebraic constructs define multiplication or exponentiation in terms of... – supercat May 26 '23 at 18:30
...limits, which might break down in cases where multiplying by integer zero would be defined as yielding the additive identity, or raising to the integer zero power would be defined as yielding the multiplicative identity, regardless of the value of the other operand. – supercat May 26 '23 at 18:31
@supercat I take your meaning, and you're right in one sense. In another sense, it's not correct to say "... are different operations". One can define these operations without relying on 'integer mult/exp is repeated add/mult', and the definitions would be equivalent (doing calculations under either system produces the exact same results and there is no way to compare inputs & outputs to distinguish the 2 without 'looking under the hood'). 'Integer mult/exp is repeated add/mult' is more a teaching/conceptual tool than a statement about fundamental mathematics. – Travis Bemrose May 31 '23 at 14:45
1

@TravisBemrose: It is useful to define a multiply-any-group-by-integer operator (which I'll denote ※) such that, for member x of any algebraic group with additive operator ℗, a 0 ※ x (with integer zero) is the group's identity, and for any integer n, n ※ x = ((n-1)※x) ℗ x. Such a definition is completely independent of the nature of the group or its operator ℗. It is also useful to define a raise-to-integer power (which I'll denote ⁂ for any element x of any algebraic ring with multiplicative operator ⊗ such that, x ⁂ 0 (integer zero) is the multiplicative identity, and... – supercat May 31 '23 at 15:48
...for any positive integer n, x ⁂ n is (x ⁂ (n-1)) ⊗ x. Note that the first of these "new" operators can be applied to any group--not just rings--and the second to any ring--not just fields. – supercat May 31 '23 at 15:52

score 33 · Answer 2 · answered May 23 '23 at 12:52

Is your variable at the base or the exponent?

An exponential function is a function of the form $f(x)=a^x$ for some constant $a$. In this case, the inverse is indeed given by a logarithm $f^{-1}(x)=\log_a(x)$.

On the other hand, if you place the variable at the base, $g(x)=x^a$, then you get what is better called (to avoid confusion) a power function, whose inverse is given by roots: $g^{-1}(x)=\sqrt[a]{x}$.

This is a nice example to highlight the importance of being precise with the terms being used. "Operation" was not defined properly, nor what an "inverse" of it should be. As a binary operation, "exponentiation" is simply the function $K(x,y)=x^y$, which is not injective and thus does not have any meaningful "inverse".

Exactly this. When people stop being imprecise, confusion vanishes. — user21820, May 24 '23 at 06:01

score 23 · Answer 3 · answered May 24 '23 at 09:02

(Despite good answers already, I thought the concrete example below could be useful.)

For multiplication and addition, there is exactly one inverse operation, namely division and subtraction.

Yet for subtraction and division, there are two possible inverse operations each. This applies to any non-commutative operation that takes two inputs.

Subtraction: x - y = z

To get x back, you compute z + y
To get y back, you compute x - z

Division: x / y = z

To get x back, you compute z × y
To get y back, you compute x / z

Exponentiation: x^y = z

To get x back, you compute z^1/y (y'th root of z)
To get y back, you compute log_x(z) (base-x logarithm of z)

(+1) Nice examples and display of them! – Dave L Renfro May 24 '23 at 10:04 — Dave L Renfro, May 24 '23 at 10:04

score 4 · Answer 4 · answered May 25 '23 at 18:39

The other answers have shown that it depends on which of the two inputs you fix and which you let vary. As a way to visualize this, here's a plot of the 3D surface $z = x^y$. I've drawn two polynomial curves: $z = x^2$ (blue) and $z = x^3$ (green), and two exponential curves: $z = 2^y$ (red) and $z = 3^y$ (purple).

To visualize the polynomial inverses (roots), rotate the whole picture so that the $z$ axis is horizontal and the $x$ axis is pointing upward. To visualize the exponential inverses (logs), rotate the whole picture so that the $z$ axis is horizontal and the $y$ axis is pointing upward.

A sideways look at the polynomial curves and their inverses, with the $y$ axis into/out of the screen:

A sideways look at the exponential curves and their inverses, with the $x$ axis into/out of the screen:

speaking of Jounce: What were Hubble's jerk and jounce limits? Did JWST have the same? — uhoh, May 26 '23 at 06:49

score 0 · Answer 5 · answered May 24 '23 at 14:31

In one case base is the variable and in the other case power is the variable. Here you are talking about an inverse of a function and not just an expression. Therefore role of variable is much important and depending on that inverse function must be different.

Why are there two inverses to exponentiation?

5 Answers5