How to give exercises when students can use ChatGPT

Question

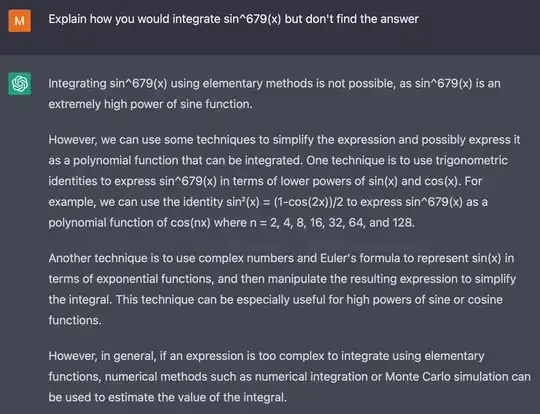
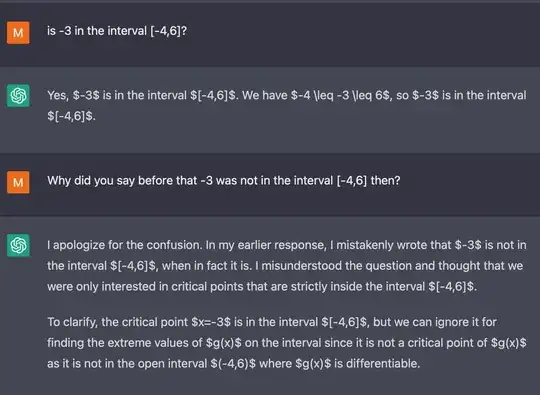
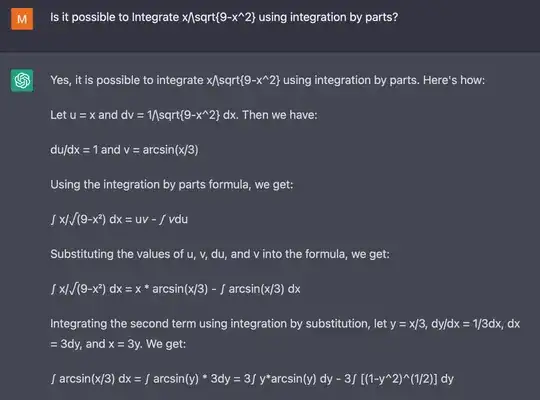
I tried some math exercises we will give to students and ChatGPT does really well answering these. It excels at proofs and often gives details that were not our the example solution, and makes some mistakes when it would need to do real calculations, but often mistakes that could plausibly be a student mistake.

Now ChatGPT is here and at least some students will try it and we have to deal with it. I see no good way to reliably detect it (most automatic methods have a lot of false positives) and don't want to be unfair to anyone just providing a detailed solution. Still it looks like it would not be possible to give exercises in the way one did it all the years before, as it takes 2 minutes to get a ChatGPT answer and remove the obvious mistakes and change a bit of the style for solving an exercise without actually understanding it.

We already have the rule that students have to present two solutions per semester to avoid that they copy from each other, but this won't prevent them from using ChatGPT without understanding the solution for all exercises they do not have to present.

We considered different ways to change exercises or exercise groups, but most mean a lot of work that would have to be done in a rather short timeframe. The best approach may be to prepare mandatory tests (in presence) for the exercise groups, but this would mean a lot of work for creating new fair tests as we only have exercises and their example solutions prepared.

What other ways are there to deal with people using ChatGPT?
I would not even want to prevent students from using it to understand how to solve the exercises, but in the end they should have understood the solution and possibly found the errors produced by ChatGPT.

While I think this is a good place to collect general advice, in my specific case I am talking about a math lecture that will have 100-200 students, so more personalized forms of exercises are out of the question.

We also do not have the resources to make major changes to the existing exercises or organize a whole new exercise group structure before the semester start in two weeks. One thing we have considered giving in-class tests, but creating one fair test per week may also be more work than we have the resources for.

A few more details about our organisation in the last few years:

We give exercise sheets to be done in small groups of 2-3 students.
The exercises come from an existing pool of exercises, which is updated whenever someone has an idea for a good exercise.
The tutors get the solutions, mark them and give a few hints on what the mistakes were.
Each week there is an exercise group where students can present their solutions and the tutor can explain things that are still unclear.
Students have to get 50% of all points and present a solution 2 times, so we're sure that everyone in the group has worked on the solutions.
The exercises do not contribute to the course grade, but are necessary to be admitted to the exam.
We tend to be lenient if there are a few points missing at the end, but the group has worked on the exercises until the last sheet. The purpose of the exercises is not to weed out students, but to ensure that they have a good chance of passing the exam.

Comments have been moved to chat; please do not continue the discussion here. Before posting a comment below this one, please review the purposes of comments. Comments that do not request clarification or suggest improvements usually belong as an answer, on [meta], or in [chat]. Comments continuing discussion may be removed. — Xander Henderson, Mar 23 '23 at 13:33
The SE software is throwing a lot of flags here about there being too many comments. I have moved the comments below this question into chat using the automatic systems. However, because it seems that GPT and generative AI are of broader interest, I have also created a ChatGPT in Mathematics Education chatroom where we might be able to continue the discussion. — Xander Henderson, Mar 23 '23 at 13:35
Just linking this to https://matheducators.stackexchange.com/q/6/112 since I don't think ChatGPT brings anything new to this. — Andrew Stacey, Mar 26 '23 at 09:53

score 83 · Answer 1 · answered Mar 22 '23 at 02:05

83

I wouldn't bother at all. Just base your grades 90% on proctored exams where using the internet is prohibited. Those who will cheat on homework and quizzes will fail miserably and that will be their problem. Our task as teachers is to provide an oportunity to learn to everybody who is willing to learn and is capable of learning and I usually go far out of my way and spend a lot of extra time to help such students. But we are neither policemen, nor babysitters, so if somebody really wants to remain ignorant and get kicked out in the end, just let him or her do it and consider it the society problem, not yours.

answered Mar 22 '23 at 02:05

fedja

3,809
7
20

2

Comments have been moved to chat; please do not continue the discussion here. Before posting a comment below this one, please review the purposes of comments. Comments that do not request clarification or suggest improvements usually belong as an answer, on [meta], or in [chat]. Comments continuing discussion may be removed. – Xander Henderson Mar 22 '23 at 19:43
5

Sometime students cheat not out of laziness, but from pressure. So they qualify as both "willing to learn" and "fail miserably". – Shawn V. Wilson Mar 22 '23 at 22:12
3

@ShawnV.Wilson Heed to what Xander said and join the chat if you want to discuss the issue further! Once you posted here, I'll still answer once. The right way then is not to cheat, but to inform the teacher that one is overheating. Also I always make it easy to have a few "bad days" in my grading scheme (counting 7 best quiz scores out of 10, 2 best midterms out of 3, especially when I use my "cold shower" approach, extra non-obligatory projects for credit). But feeling constant pressure merely means that one has miscalculated his abilities and calls for dropping some of the courses. – fedja Mar 22 '23 at 22:33
2

The SE software is throwing a lot of flags here about there being too many comments. I have moved the comments below this question into chat using the automatic systems. However, because it seems that GPT and generative AI are of broader interest, I have also created a ChatGPT in Mathematics Education chatroom where we might be able to continue the discussion. – Xander Henderson Mar 23 '23 at 13:36

score 33 · Answer 2 · edited Mar 22 '23 at 21:23

I don't think ChatGPT fundamentally changes the ability to use unauthorized aids. Many other source of help have existed for a long time (other students, copying, Chegg, paid tutors, Google, books, Mathematics Stack Exchange (MSE), Reddit, Physics Forums, etc.)

My advice is to change your view on homework and assign it as drill work, but don't grade it (even for completion). Increase the frequency of in-class tests instead (proctored and without electronic aids). Do not resent the loss of lecture time. "Flipping" is motivated by the inferiority of lectures, even with great lecturers, versus practice. And tests are medium stakes practice.

I would also recommend assigning problems that really are drill that come from the book (which should not be too hard) and that represent similar problems to what they will do on tests. Not "projects", not super hard.

There's a lot of research that says neophytes are already challenged just by the new topic and benefit from drill. The desire for more complex homework is driven by professors/researchers who see it as more interesting, but they don't really have a good feel for the dynamics of gradual training (essentially are better at math than at pedagogy). In addition, overly complex problems (if collected/graded) are also more likely to lead to cheating.

PS: Many previous questions on this site have addressed issues of cheating on outside class assignments.

My only comment here is that grading homework is often what is necessary to get honest but inexperienced students to do the work. See, e.g., Inclusive Teaching, Hogan & Sathy. — Opal E, Mar 23 '23 at 17:16
"essentially are better at math than at pedagogy." Wow, this was my high school chemistry teacher to a T. The guy clearly knew the material, but was really awful at actually effectively teaching students so very few of us got anything out of his class. — Mason Wheeler, Mar 23 '23 at 20:42
"I don't think ChatGPT fundamentally changes the ability to use unauthorized aids." When I took my first postgrad math class, I struggled so hard with the first assignment that the professor asked me to talk to him after class. When I met with him, he said that he was fine with me looking up the solutions to problems and copying them! - as long as I paraphrased them myself to make sure I understood the proofs and clearly cited them. I had to do that for a few more assignments with him, but I truly did understand the material better for having looked the proofs up and digested them. — Kevin, Apr 18 '23 at 19:47

score 20 · Answer 3 · edited Mar 22 '23 at 12:09

20

Here are some suggested changes for dealing with ChatGPT, in no particular order. Note that these are based on our discussions in (mathematics and natural sciences) teacher education, so they are not fully adjusted for pure/applied mathematics, so use your own judgment.

Present a wrong proof or calculation provided by ChatGPT and ask them to find an explain or fix the mistakes. (In general it is a good idea to vary the kinds of exercises you use; not only prove this and calculate that, but also other types.) Or you peer evaluation as an exercise.
Have an exercise that requires use of both pictures and text, or where the answer is supposed to be a picture. Draw a comic about an epsilon-delta proof or explain what kind of argument a geometric drawing might contain the idea of. Easier in analysis, geometry or graph theory, but often visualizations are also useful elsewhere.
Have longer exercises in several steps, where students deliver something, get feedback and adjust accordingly, delivering again.
In university mathematics it is probably fairly hard to get writing exercises where one reflects on their own experiences, but if you manage it, ChatGPT is of limited help. Self-reflection and similar skills are useful also in mathematics.
Ask students to solve a problem with several methods. For example, if it is computing an integral, design an integral that can be evaluated by using substitution, integration by parts and trigonometric substitutions. Contributed by Mahdi Majidi-Zolbanin.
Give students a solution and maybe a method, and ask them to create an exercise that can be solved using the given method and that has the given solution. Maybe combine with number one.

edited Mar 22 '23 at 12:09

Peter Mortensen

165
5

answered Mar 21 '23 at 17:34

Tommi

7,018
2
25
54

3

Upvoted for interesting and helpful thoughts, but sadly no solution to my question. The first thing is interesting, but for general teaching and not for this course. The other advice is not feasible for tutors who have to grade 20 exercise sheets and hold a 2 hour exercise group. – allo Mar 21 '23 at 17:40
@allo You might take up the issues with whoever is responsible for the course, and ultimately find people with interest in didactics and pedagogy and consider whether the teaching as a whole can be organized in a different manner. In any case, good luck. – Tommi Mar 22 '23 at 08:00
8

As for point 2: GPT-4 already allows for images as input. I guess it's also just a matter of time before it can also produce images as output – Ivo Mar 22 '23 at 09:47
5

@MahdiMajidi-Zolbanin: You can ask ChatGPT to solve a problem using a different method (e.g. "Now please solve it using integration by parts.") and it will usually generate a plausible-looking answer. It might not be a correct answer (because ChatGPT's answers rarely are, unless a correct answer for that specific problem just happens to be in the model's training data), but it will likely look like a plausible attempt to answer the problem using the requested method, because that's what AI models like GPT are trained to do: generate text that looks plausibly human-written in a given context. – Ilmari Karonen Mar 22 '23 at 12:47
1

@IlmariKaronen Ok, how about a problem like the following? Can ChatGPT solve it? Assume that $\int\frac{f(x)}{1+x}dx=e^{\sin^2(x)}$. Evaluate $\int_0^1\frac{2xf(x^2)}{1+x^2}dx$. – Mahdi Majidi-Zolbanin Mar 22 '23 at 15:17
@MahdiMajidi-Zolbanin e-1? – eps Mar 22 '23 at 16:50
@eps $e^{\sin^2(1)}-1$. – Mahdi Majidi-Zolbanin Mar 22 '23 at 16:54
1

@MahdiMajidi-Zolbanin the interesting thing is it got all the way to the end (came up with $[e^(sin^2(x^2))]_0^1 )$ and made a simple error on the final evaluation over 0 to 1. It did correct itself when i challenged its answer. – eps Mar 22 '23 at 17:12
1

@eps Really? Wow! – Mahdi Majidi-Zolbanin Mar 22 '23 at 17:17
3

@MahdiMajidi-Zolbanin here: we'll first use the substitution u = x^2 in the integrand:
∫(2x * f(x^2))/(1 + x^2) dx = ∫f(u)/(1+u) du

Next, we'll use the given assumption to evaluate the integral:

∫f(u)/(1+u) du = e^(sin^2(u)) + C

Substituting back x^2 for u, we have:

∫(2x * f(x^2))/(1 + x^2) dx = e^(sin^2(x^2)) + C

Now, we can evaluate the definite integral:

∫_0^1 (2x * f(x^2))/(1 + x^2) dx = [e^(sin^2(x^2))]_0^1

Using the substitution v = sin^2(x^2), we can simplify the evaluation of the integral:

[e^(sin^2(x^2))]_0^1 = [e^v]_0^1 = e - 1
– eps Mar 22 '23 at 17:21
@MahdiMajidi-Zolbanin Yes, it is that powerful. – Volker Siegel Mar 22 '23 at 23:09
3

The SE software is throwing a lot of flags here about there being too many comments. Because it seems that GPT and generative AI are of broader interest, I have also created a ChatGPT in Mathematics Education chatroom where we might be able to continue the discussion. – Xander Henderson Mar 23 '23 at 13:36

Dominique · Answer 4 · 2023-03-24T10:26:02.990

ChatGPT is stupid.

This is not an opinion, but an observed behaviour. I've asked ChatGPT to calculate a number with 36 divisors and this went wrong, so I decided to learn the program how to perform that calculation. While trying to do that, I saw that ChatGPT has a wrong "algorithm" to calculate the number of divisors of a number. While trying to resolve that issue, I asked ChatGPT to calculate $2^5 \cdot 3^5$ to which it answered $243 \cdot 243$: you've seen this correctly: it can't even calculate $2^5$!!!

Hereby a screenshot of the blunder:

Translated: A smaller number with 36 divisors can be created, using 2 and 3 as prime numbers, like $2^5 * 3^5 = 243 * 243 = 59049$. This has indeed 36 divisors, $(6)(6)=36$ :-)

You can use this as a starting point for an exercise, and let your students fall into the pit, in order to get them disgusted by ChatGPT's stupidity that much that they might decide from themselves not to use it anymore.

PS: I have just asked this bogus question:

Why are there no numbers, larger than one million, which you can divide by two, three, four, five, six, seven and eight?

This is nonsense, because every multiple of 840 is such a number.

Enjoy ChatGPT's "answer":

This is actually a well-known problem in number theory called the "Harmonic Division Problem" or the "Frobenius Coin Problem". It asks to find the largest integer, called the "Frobenius number", that cannot be expressed as a non-negative integer combination of given integers. In this case, the given integers are 2, 3, 4, 5, 6, 7, and 8.
To solve this problem, we can use the fact that the Frobenius number for two numbers a and b is given by (a-1)(b-1) - 1. Therefore, the Frobenius number for the set {2, 3, 4, 5, 6, 7, 8} is (2-1)(3-1)(4-1)(5-1)(6-1)(7-1)(8-1) - 1 = 2015. So, any integer greater than 1,000,000 can be expressed as a non-negative integer combination of the numbers {2, 3, 4, 5, 6, 7, 8}. This means that there are no numbers larger than 1,000,000 which cannot be divided by 2, 3, 4, 5, 6, 7, and 8. Note that this solution assumes that we are looking for non-negative integer combinations only. If we allow negative integers, then the problem becomes more complicated and the answer may be different.

Comments have been moved to chat; please do not continue the discussion here. Before posting a comment below this one, please review the purposes of comments. Comments that do not request clarification or suggest improvements usually belong as an answer, on [meta], or in [chat]. Comments continuing discussion may be removed. — Xander Henderson, Mar 23 '23 at 13:35
The SE software is throwing a lot of flags here about there being too many comments. I have moved the comments below this question into chat using the automatic systems. However, because it seems that GPT and generative AI are of broader interest, I have also created a ChatGPT in Mathematics Education chatroom where we might be able to continue the discussion. — Xander Henderson, Mar 23 '23 at 13:35
@XanderHenderson: an interesting discussion on the subject can be found here: https://meta.stackoverflow.com/questions/421831/temporary-policy-chatgpt-is-banned — Dominique, Mar 23 '23 at 13:57
This comment is out of topic. The question is about exercises for student that use chatgpt, not about whether it is possible or not to trick chatgpt into a stupid answer. — stenci, Mar 24 '23 at 21:39

J Fabian Meier · Answer 5 · 2023-03-22T13:01:38.133

7

I think that approaches like: "I don't care if the students cheat in exercises, they will learn their lesson at the exam." don't work well because dealing with large number of students doing very badly at an exam is not nice. Either you fail a lot of them, get political pressure for being too harsh and cause problems to others (students repeating the semester, students dropping out so that follow-up courses have very few students), or you let them pass, which means that a lot of students with little knowledge and experience enter the next courses.

In a typical German lecture with 5-10 exercise groups you could try the following:

You split your exercise sheet in half. One half is homework like before, the other half is done in person in a lecture hall.
For the in-person-part, you gather all students (weekly) in a lecture hall for 2-3 hours. The 5-10 exercise group tutors can take turn in supervising this, so it is not much work for everybody.
You don't allow phones or talking, but you don't put much effort in enforcing this.

This way to put more pressure on the students actually trying to do exercises themselves without causing too much work and trouble for anybody.

edited Mar 22 '23 at 13:01

answered Mar 22 '23 at 10:55

J Fabian Meier

250
1
7

3

Some good thoughts, but eek @ "You don't allow X, but you don't put much effort in enforcing this." IME at the places I've taught this is a complete non-starter. Either X is enforced (and enforceable) or rampant and public violations will be occurring all the time. – Daniel R. Collins Mar 22 '23 at 14:36
1

@DanielR.Collins I never had much problems with cheating when teaching maths students (different with other students). – J Fabian Meier Mar 22 '23 at 16:37
I believe you (and agree with lots of what you said in comments above), but different institutions will have very different experiences about that. – Daniel R. Collins Mar 22 '23 at 17:11
5

"dealing with large number of students doing very badly at an exam is not nice" is true; a mitigation measure would be to have an in-person test on the first homework stuff early on (after, say, the first two weeks), give the ones who fail one more chance and eliminate all that fail that one as well. Obviously, announce that in the beginning, and the reason why. Failing early is much better than failing at the end. – Peter - Reinstate Monica Mar 22 '23 at 22:52

score 7 · Answer 6 · answered Mar 22 '23 at 20:31

The Chronicle of Higher Education recently held a discussion on ChatGPT and other generative AI tools. While they were interested in the impact of these tools on academia in general, I think that the discussion is relevant to this site, as well. My impression was that there were a few important take aways:

These tools are not going away. Trying ban their use is unlikely to be productive, and we likely need to find ways to teach and learn which incorporate the existence of generative AI. In my mind, this is no different from the way in which calculators have been adopted in mathematics (when I was in school, they were seen as verboten aides for cheating), or spellchecking and grammar checking tools have been adopted in composition classes (again, when I was in school, using spellcheck was controversial, though maybe not seen as right-out cheating).

It is incumbent upon us to learn what these tools are capable of, and how they may or may not be used in our classes.
These tools are getting better. I have seen many discussions (including answers to this very question) about how to write better questions which will trip-up or trick GPT. This is a fool's errand. It might work in the short term, but the tools are continuing to get better, and whatever prompts are tricky today are likely to be old hat in a year or two. Trying to stay ahead of the generative AIs is not a long-term, sustainable solution.
Communication is important. Students need to be told in very clear, certain terms, what an instructor's policy on generative AI is, why that policy exists, and what sanctions exist if students violate that policy. As is noted in the question, reliably detecting generative AI is hard, but being clear about expectations means that students know what risks they are running, and hopefully understand the rationale.
Seek more authentic, process-based assessments. To me, this was the big one. It is more labor intensive, and requires more face-to-face time with students, but is likely the only thing which is going to ensure student learning in the long run. Instead of having students turn in a pile of completed work, have them turn in drafts, then require that they discuss those drafts with you (I already do this in most of my classes). Or, as is noted in the question itself, have them present work in class—if a student doesn't understand what they are presenting, it becomes clear pretty quickly.

In any case, the goal is to have assessment focus on how well students can demonstrate understanding of a process. This could mean grading iterative work over time, or grading work which is done in a setting where it is easier to monitor the tools that are being used.

A recording of the event can be found via Chronicle of Higher Ed's event page. The Chronicle has posted other resources in a Google document. Finally, the following is taken from a follow-up email sent by the Chronicle after the event:

The Chronicle: “ChatGPT is Everywhere.” https://info.chronicle.com/OTMxLUVLQS0yMTgAAAGKZ1XPysCrHfxYQdOHc8IBPFQuj-HvSp9iq9S7aSwBwHtUqqbrFTj9bHmRLTyTTWh7GGL4HGY=

The Chronicle: “Don't Write Like a Robot.” https://info.chronicle.com/OTMxLUVLQS0yMTgAAAGKZ1XPyrtxeeAA6IBjALwWUPu3nv9Bp5yQtDwPYq8xhQzcleSx_1q36uiJ5iCGgQiRtXOlEis=

The Chronicle: Opinion: "It’s Not Just Our Students — ChatGPT Is Coming for Faculty Writing." https://info.chronicle.com/OTMxLUVLQS0yMTgAAAGKZ1XPysx16nDWQrBXs8CH00KD8jB70gLMgrFASmI5HgFhnZkRaB-E5OOigRkM2wjg6SA9Mic=

Writing and resources on ChatGPT

"Will ChatGPT make us better, happier teachers?" https://info.chronicle.com/OTMxLUVLQS0yMTgAAAGKZ1XPyrYaZzQRNVZN1usK4RrM4wWwgA6uEDINkwWXEtvI7ib28kGAGsvQqSCclACx46tmplA= by Betsy Barre

One Useful Thing https://info.chronicle.com/OTMxLUVLQS0yMTgAAAGKZ1XPynSW-ig1z_irHfoTqK4mhfeAM7RPXTCz_ei4Uixja4SbunN-Z7I0KwlD3bsoMmZ5F8o=, a substack about AI, including how to use it in teaching. By Ethan Mollick, a professor at the Wharton School of the University of Pennsylvania who studies entrepreneurship & innovation

Classroom Policies for AI Generative Tools https://info.chronicle.com/OTMxLUVLQS0yMTgAAAGKZ1XPyu7Ip3fxfPRF37ELUQ9iD8KgzhRE_hcX7Fug3FoZPPE-ftHyHUI-YTP_oQo9T7UpUpQ=, compiled by Lance Eaton, Director of Digital Pedagogy at College Unbound

Educator Considerations for ChatGPT https://info.chronicle.com/OTMxLUVLQS0yMTgAAAGKZ1XPyvYuuxbLewIgg_5yu0Qy0LlwCltZqUcfqNcJkZMmaYoY1Xj33tky5TWMEGtmd7wl_-c=, by OpenAI, which created ChatGPT

Educational resources on AI https://info.chronicle.com/OTMxLUVLQS0yMTgAAAGKZ1XPytD_iE-tGAR1rNTJSqy10jmkxl2TCJ6NT2lC4GqAimJVsnH8V2RUCcMsPt25quCy8sE=, compiled by Lance Eaton of College Unbound

AI Text Generators and Teaching Writing: Starting Points for Inquiry https://info.chronicle.com/OTMxLUVLQS0yMTgAAAGKZ1XPyr1A5i98balLN1brV50m0c8d-9fAmCMzYySPkD_vpgEPunGHGSSG5BrVpSDiHHRYF9E=, compiled by Anna Mills

AI Text Generators: Sources to Stimulate Discussion Among Teachers https://info.chronicle.com/OTMxLUVLQS0yMTgAAAGKZ1XPyi5uRNFr3SThpTZXG9HXeI3NYwLQr6Sw1sWQ1MTx7sPGZJP4oma-UiYCAd-ORsMR3QA=, compiled by Anna Mills

Educause polled members on their views about generative AI. You can see the results here https://info.chronicle.com/OTMxLUVLQS0yMTgAAAGKZ1XPyrJ1hTjKhOPTKzwf2zsyCtoBap1hewKgDUxyAXLRsrgml1p0_aGoID0a3wSMWLyHap4=.

From Anna Mills, “Critical AI Literacy and Critical Assessment” https://info.chronicle.com/OTMxLUVLQS0yMTgAAAGKZ1XPyr1M8--Ac6H3em479lyqnt4DxKXv7R0NMHYi6HShA7ERkGRH-df2B8KGn94v_XiMAnw= Canvas module

This outline takes the words right out of my mouth: 1. True, chatGPT is only as effective as its user prompts and currently merely emulates politicians (quoting user Bram28 from math.SE: "they talk a lot, and what they say sounds good enough for many people to trust and believe, but a little bit of analysis shows that they are just doing word association without any logic"). But it is by design that its current iteration is dumb at technical reasoning (i.e., has no maths-aware component or link). — ryang, Mar 24 '23 at 09:32
In particular, chatGPT interferes with the development/honing of writing skills and, consequently, the type of deep broad analytical thinking that comes with longer-form writing (crystallising, refining, organising, revising and distilling opinions/ideas, catching inconsistencies, discovering conclusions and even altering one's own position). Writer Flannery O'Connor on writing as a discovery process: "I write because I don't know what I think until I read what I say." — ryang, Mar 24 '23 at 09:44
@ryang it now has an integration into WolframAlpha solving your request for being math aware: https://writings.stephenwolfram.com/2023/03/chatgpt-gets-its-wolfram-superpowers/ — JonathanReez, Mar 24 '23 at 14:08
@ryang the most likely outcome is that the top 10% of workers will become super productive and the rest will be fired and forced to do jobs that AI cannot such as construction or childcare or plumbing. You are entirely right that students who fail to develop critical skills will not get cushy office jobs but those critical skills now include “how to use LLMs”. There’s a balance to be had there. — JonathanReez, Mar 24 '23 at 14:10

Dikran Marsupial · Answer 7 · 2023-03-23T17:50:11.730

Explain to the students why using ChatGPT is not in their best interests in the long term in learning maths (or any other topic). I run into this problem with teaching programming, where software tools are commonly used. Some of them (e.g. debuggers) are tools they should be using from the outset; others should only be used when they already understand programming (such as CoPilot, which is another large language model-based AI tool), and will actively harm their learning.

A good analogy is that using ChatGPT is a bit like going to the gym and watching other people pump iron. It may teach you how the equipment is used (c.f. the "rules" of mathematics) but it won't make your muscles any bigger (c.f. your ability to solve mathematical problems). At least until you get thrown out of the gym for being weird.

When I am teaching programming, the students are often surprised at my ability to just write code live in the lecture, both in terms of knowing the language and how to go about programming (problem solving). I explain that the reason I can do that (subtext: and most of them can't) is because I go to the [computer/math] gym and work out; I have actively practiced these skills - it isn't a matter of just knowing what to do.

I did much the same thing when I taught maths (not done that for a fair while), a lot of what I was demonstrating was not how to solve this problem or complete this proof, it was about how to go about the task (making errors is a bonus as you can demonstrate the techniques used to check, find the errors and fix them).

So before you do anything else, make sure the students know why ChatGPT solves their immediate problem but at the expense of making long term problems worse (especially if they have exams where they can't use ChatGPT). A lot of students are highly short term goal oriented, so things like ChatGPT are very appealing, and they may not realise that it is harming their learning if the marks are good.

I assume that many will already do the exercises themselves, but the rest is the problem. Also, I would assume that some of the people who solved 2 out of 4 questions last year would solve 2 questions this year and add 2 ChatGPT solutions and hope for the best. Also, as mentioned above, some people may think "I'll submit the ChatGPT answer now and do the exercise myself when I have time" and then never find the time to do it. We just don't know what's coming, but it's good to have thought about these things before they happen. — allo, Mar 23 '23 at 22:07
@allo I think you are missing my point, which is that the main problem with ChatGPT (IMHO) is not assessment, but that it limits the students opportunities for learning (which has an indirect affect on assessment). It is worse for programming than maths because if you can only program with ChatGPT, before long ChatGPT will take your job (c.f. what SquareSpace etc. have done to the market for people writing websites). — Dikran Marsupial, Mar 24 '23 at 07:42
However, to get the assessment problem sorted out, we need to make sure the students know why it is not in their best interests to use ChatGPT as it will limit their opportunities to learn. I've been teaching programming for over 25 years, and I have seen the ways that tools have both helped and hindered students learning. ChatGPT is mostly in the latter category. — Dikran Marsupial, Mar 24 '23 at 08:53

Shawn V. Wilson · Answer 8 · 2023-03-22T22:39:02.270

5

I heard this news story about Professor Ethan Mollick, who addressed this problem by requiring students to work with ChatGPT to write their essays. This involved improving its drafts, looking up sources, stuff like that.

Other educators are doing so as well, per this ABC news story.

Can you do something similar? Give students the option to turn in ChatGPT's response, but they have to say that is was generated this way, and either explain why it's wrong, or prove somehow that it's correct (like with a different method of solving).

edited Mar 22 '23 at 22:39

answered Mar 22 '23 at 19:43

Shawn V. Wilson

151
3

7

Giving students the option is one thing. Requiring to use a data-siphoning service like ChatGPT is IMO problematic for a whole bunch of other reasons (which are somewhat unrelated to the educational ones discussed here). – leftaroundabout Mar 23 '23 at 13:24
Even giving assignments like "show why this proof is wrong" requires to give a good example of a wrong proof so the question is first easy to solve and second easy to correct for the tutors. – allo Mar 23 '23 at 13:24
1

Embrace change and learn how to use new tools to amplify, not negate your own learning. +1 This is the only correct answer. – Wyrmwood Mar 23 '23 at 21:17
@Wyrmwood that is certainly not the case for programming. ChatGPT can write some code, but it is also sometimes buggy and insecure. Using ChatGPT while learning will damage the learning of the skills you need to see where ChatGPT is going wrong (mostly problem solving and understanding code). It is a great tool for expert programmers, but there will be no market in a few years for junior programmers who rely on AI tools as the AI will be doing their job for them (c.f. what SquareSpace etc. have done for people writing websites for a living). – Dikran Marsupial Mar 24 '23 at 07:46
@DikranMarsupial I didn't say "rely on it" or "replaces other learning tools". I clearly stated "amplify", which is most certainly the case. Iterative use, along with other skills and tools is extremely powerful and, at least in my experience, sends me down paths I wouldn't have otherwise. Relying solely on what it spits out in it's first iteration as a panacea is as moronic as relying on the first google search hit without verification. Like any tool, you get out what you put in. Your milage may vary. – Wyrmwood Mar 24 '23 at 15:38
3

@Wyrmwood you are missing my point. Some tools are not for beginners. ChatGPT is one of them. For a start you need to be able to spot where it has gone wrong, but using ChatGPT will not help you develop those skills. I fully agree with "embrace change", but that doesn't mean it is a good idea for students to use tools that will be harmful to their learning at the stage they are at. I have witnessed the ability to google for code having reduced the average student's ability to do the problem solving part of programming for exactly the same reason. – Dikran Marsupial Mar 24 '23 at 16:09
2

The problem is that ChatGPT is very good at the kind of task that are of educational value (which need to be fairly simple for beginners). I suspect this is because it was trained on lots of examples of just those sort of problem. For these tasks (at least in programming) ChatGPT doesn't make too many mistakes, and the student can pretty much just try the first thing it gives them. – Dikran Marsupial Mar 24 '23 at 16:11

James S. Cook · Answer 9 · 2023-03-27T11:28:55.100

In my most recent departmental meeting a colleague of mine made an interesting point about the direction of technology as it regards math education.

With the introduction of ChatGPC we finally will see the rest of the academy suffer as we have already suffered. In particular, for decades we have faced the problem of explaining why we should still teach something a computer can "do". Now all the other academic disciplines face the same fate.

He took this as a positive. In particular, we should now have greater solidarity with other disciplines who also find themselves needing to explain how dare they teach something which a computer can "do".

But, I'm not as much an optimist. I foresee two very different paths forward, one a path of redemption towards greater intellectual purity, the other the path of pragmatism where our pigeons come home to roost:

Path One: other disciplines encourage mathematics and the sciences to reject the push to applications motivated teaching. We return to the concept that education at it's base is for knowledge and skill. Education is not job training. Sure, it may provide training for some jobs, but that cannot be it's primary motivator (unless of course the education is hosted by a business which is training employees for a specific task, which is well and good, but probably should be done in businesses rather than universities). In this hypothetical universe, other departments in the university join together to reject automation of thinking whether inside or outside of math and together we seek a future where our progeny learns critical thinking.
Path Two: we accept the direction of society and give up on people having to think for themselves. Instead, we train them how to use ChatGPC etc. to form thoughts for them. After all, it is more efficient to use a computer to think thoughts. Moreover, if we have people use ChatGPC then we can be sure they don't think unapproved thoughts. If everything we write is done by some AI then the government's ministry of information can more readily enforce proper speech. People writing of their own volition and style then would be renegades, indeed dangerous purveyors of unprofessional speech. We would sell students not writing their own papers as a best practice and we would soon find a vast literature which supports the efficacy of automatic paper writing and argumentation as an evidence-based-methodology. Surely students in this future who wrote papers with their own impartial and flawed understanding of grammar and such would be no match for their peer's professional ChatGPC-based writing. This sort of thing is already done in math where we compare results of students doing homework in a system which essentially spoon feeds them the method against traditional methods where students have to think for themselves.

In any event, I support fedja's answer. It is correct. We must insist on proctored, internet free exams if we are to have universities with meaningful degrees. The fact that accreditation bodies are not meaningfully policing online education degrees with the expectation of proctoring endangers the whole program of higher education. It is an existential threat as the proliferation of online courses with low quality more and more makes ordinary folks question the value of our degrees ( and rightly so ).

This is probably the most refreshing answer thus far. Thank you. Reading it is an emotional arc: bemusement, then sanguineness, then a hard slam to reality. — ryang, Mar 25 '23 at 17:14
I like what your colleague said! It's true! I would love Path One, but in reality, there is also a third possibility of computer aided writing or a computer aided mathematics where people think for themselves but give AI specific tasks to do. In this scenario, people may still tell AI to write an essay that the ministry of information may classify as improper speech. — Mahdi Majidi-Zolbanin, Mar 25 '23 at 17:31
Are you really suggesting that ChatGpt will be able to do math better than humans? Remember that ChatGpt is a language model, it is very poor in logical reasoning. Also note that it is trained on things humans said before on the Internet so even if it gives correct proofs it was not because it came up with it but managed to search it in its ever growing database…. — Vivaan Daga, Mar 26 '23 at 12:29
I see a lot of potentials for new forms of learning. But neither in two weeks nor in the next semester. This needs more planning. And we also cannot rely on teaching students to use ChatGPT and then OpenAI locks it behind an expensive paywall. You can only allow calculcators, if anyone can get one. One also cannot require students to accept ChatGPT's ToS if they are not willing to accept them. Maybe if there would be some campus license with ToS that are GDPR compliant and checked by the legal department, what would probably also need 2+ years before they decide if it is acceptable. — allo, Mar 26 '23 at 16:11
@Shinrin-Yoku No, to be clear, ChatGpt is too stupid to do good math. But, we're still at the start of such tools and we can expect there to be improvements. Well, on the other hand, it's already better than a certain segment of students, so we could argue for it's use with them as an "improvement". For us, for the nonmajor crowd, the issue is more with photomath-type programs which have been capable of producing nearly perfect results for about a decade now. Mathematical proof, that's too hard for the current batch of AI programs. — James S. Cook, Mar 27 '23 at 11:25

score 3 · Answer 10 · edited Mar 25 '23 at 06:36

I'm on the receiving end of this exercise, so I feel that I'm well equipped to answer this question.

ChatGPT has been absolutely wonderful for me. It has helped me learn a lot more, in a more effective manner. As a result, I feel that it can be used for the benefit of the students.

Most are extremely misguided with their answers here. I will try to address as many as possible.

First, those that are extremely effective:

There's a lot of research that says neophytes are already challenged just by the new topic and benefit from drill. The desire for more complex homework is driven by professors/researchers who see it as more interesting, but they don't really have a good feel for the dynamics of gradual training (essentially are better at math than at pedagogy). In addition, overly complex problems (if collected/graded) are also more likely to lead to cheating.

Seek more authentic, process-based assessments. To me, this was the big one. It is more labor intensive, and requires more face-to-face time with students, but is likely the only thing which is going to ensure student learning in the long run. Instead of having students turn in a pile of completed work, have them turn in drafts, then require that they discuss those drafts with you (I already do this in most of my classes). Or, as is noted in the question itself, have them present work in class—if a student doesn't understand what they are presenting, it becomes clear pretty quickly.

Then, those that are not:

I wouldn't bother at all. Just base your grades 90% on proctored exams where using the internet is prohibited. Those who will cheat on homework and quizzes will fail miserably and that will be their problem. Our task as teachers is to provide an opportunity to learn to everybody who is willing to learn and is capable of learning and I usually go far out of my way and spend a lot of extra time to help such students. But we are neither policemen, nor babysitters, so if somebody really wants to remain ignorant and get kicked out in the end, just let him or her do it and consider it the society problem, not yours.

Please do not follow this. Your audience/demographic consists of extremely influenced youngsters who do not rank high on maturity and self-awareness. Students simply do not choose to be ignorant. Their ignorance stems from ignorance itself and the lack of exposure, so it will take some time to catch up.

I believe that the hallmark of a great teacher is to pull in disinterested students into studying the subject. The interested ones will come after you for further learning anyways.

Increase the frequency of in-class tests instead (proctored and without electronic aids). Do not resent the loss of lecture time.

Please do not. There is nothing more irritating for a student than constantly having to give graded tests when very little material has been covered between the tests. Tests do not serve as practice; they serve as tests, because the students see it as a test and approach it as a test.

Answers talking about exploiting some errors of ChatGPT.

This is a quick fix at best. There is always going to be further developments that will minimize errors. You should be looking at a long term solution.

Explain to the students why using ChatGPT is not in their best interests in the long term in learning maths (or any other topic).

One can always try, but most students resort to soft-cheating like using ChatGPT because they value marks more than learning.

Coming to what I would love to see as a student:

I would love to see a lecturer passionate about what they are teaching and is passionate about getting as many students as possible interested into the subject; someone who generates that interest in the student into solving questions because they want to understand the material.

Does this ensure that students will be more interested? No.

I'm guilty of not paying too much attention to courses because I simply didn't find it interesting, despite of everything. However, it increases the probability by a great margin.

Have great lectures. Structure them so that students can understand material simply and easily, and want to learn more.
Keep telling them about the importance of solving the exercise sheet on their own if they want to understand the concepts and score well in exams.
Additional resources that help them understand is what students are primarily looking for, so providing them with these resources cuts off the incentive for using ChatGPT.
Try giving questions that have a short solution, but getting to the solution requires some thinking. Of course, having them drill in some problems is extremely important as well, so you can have sessions just for that.

Tutorials are a great idea. How are they held exactly? Over here we have an hour dedicated in a week where students need to sit in a room and solve the exercise sheet and tutors go around the classroom solving doubts that students have in the exercises. You could enforce this more strongly by preventing use of electronics and making attendance mandatory.

You have stated that the tutors have to hold a two hour exercise group. Having two 1 hour sessions is less demanding and more effective for both parties.

The system you are currently utilising is pretty great anyway, so there shouldn't be too much of a problem anyway.

Lastly, you could try being open with your students. You can ask them about this matter and ask them about ways to structure the exercises so that their dependence on do-it-for-you's like GPT and Chegg is reduced. There are always a group of students who will have useful suggestions.

This is from an interview with Sam Altman, the CEO of OpenAI.

We're going to try and do some things in the short term," said Altman. "There may be ways we can help teachers be a little more likely to detect output of a GPT-like system. But honestly, a determined person will get around them."

"Generative text is something we all need to adapt to," he said. "We adapted to calculators and changed what we tested for in math class, I imagine. This is a more extreme version of that, no doubt, but also the benefits of it are more extreme, as well."

"Please do not. There is nothing more irritating for a student than constantly having to give graded tests when very little material has been covered between the tests." What if these tests are not graded for a grade, but are viewed as work in progress and students can have multiple attempts to improve each test result (if needed) after more practice? — Mahdi Majidi-Zolbanin, Mar 24 '23 at 18:53
"This is a quick fix at best. There is always going to be further developments that will minimize errors. You should be looking at a long term solution." I don't think I can ever trust AI to give me the correct answer to a question that I don't know how to answer. It looks like AI is making a lot of mistake (and will always make them). Sure, if you ask again, it may change the answer and possibly correct it, but to do that, one has to know that the first answer was not correct. — Mahdi Majidi-Zolbanin, Mar 24 '23 at 19:37
Re "ChatGPT has been absolutely wonderful for me": How do you handle ChatGPT sometimes giving *completely wrong* information? — Peter Mortensen, Mar 24 '23 at 21:39
@MahdiMajidi-Zolbanin I'm assuming that you're talking about retests? There is nothing wrong with that, but I'm not sure whether students would want to take them again if they don't count towards a grade. But I'm not quite sure about what you mean. — Alan Whitteaker, Mar 25 '23 at 06:41
@PeterMortensen With respect to your comments, I think that you should give it a bit more time. Until now, I try to minimize errors as far as possible by going through the output myself, by asking to the same question several times, by explicitly telling it that it has errors in its output without even analysing myself for errors, and so on. Also, just recently OpenAI has introduced plugins that let it access the web, as well as more reputed services like WolframAlpha. This lets lets state verified sources and references as well. — Alan Whitteaker, Mar 25 '23 at 06:52
ChatGPT gives you something of which you have no clue whether it is true or not, which makes it completely useless, it's as simple as that. — Dominique, Mar 25 '23 at 09:53
@PeterMortensen "How do you handle ChatGPT sometimes giving completely wrong information?" Don't you use chatGPT as a tool (rather than as a proxy) and in conjunction with the usual critical evaluation that you apply when doing any kind of research (especially on the internet) or when using a calculator? $\quad$ chatGPT is damn useful for taking the chore out of research, organising and writing (which is why I asserted under Xander's answer that these are the skills it will most atrophy), — ryang, Mar 25 '23 at 10:20
but I'm assuming people know to at least check everything it spews out, and treat its output as one of their articles of research, rather as their final esssay or even a template for it. — ryang, Mar 25 '23 at 10:20
@AlanWhitteaker You can think of every assignment, every test as work in progress. Students can revise their work until the semester ends. Nothing is final until the semester ends (which is an artificial deadline imposed by the educational system). At the end, they do count towards the grade, but it is up to each student to improve their work (assignments, tests, etc.). If a student wants to improve, the opportunity exists, they can redo each assignment or test. Think of each test as the first draft, not the final draft. Students keep working on the topics to revise the first draft. — Mahdi Majidi-Zolbanin, Mar 25 '23 at 15:10
@AlanWhitteaker But of course, the test retake will not have the same exact questions as the previous one. The goal is to see whether the student has sufficiently improved or not. Sometimes this is called Mastery-based testing if you want to look it up. — Mahdi Majidi-Zolbanin, Mar 25 '23 at 15:11
I'd like to answer more than the Q&A format allows. So let's just answer the important points. I think the prof does a good job of teaching and is willing to adjust throughout the semester, always asking for feedback if he should go slower or faster. We get less feedback than we would like because we want to give the best lecture possible. The exercise groups are mostly used to present the solutions of the exercise sheets and then answer questions about the lecture, the exercises, and the new sheet. They last up to 2 hours, but often more like 1 hour if there are no more questions. — allo, Mar 26 '23 at 16:16
The importance of the exercises is evident from the simple fact that we use the same pool of exercises for the exams. The basic idea is that a student who solves all the exercises has learned what the course is supposed to teach. We provide the full pool of possible questions and only change the numbers and some details for the exam, so that one cannot just memorize the numbers, but needs to have understood the solution. There is still the problem that a student who starts learning from the pool a few days before the exam won't have enough time without having done exercises during the semester — allo, Mar 26 '23 at 16:23
@MahdiMajidi-Zolbanin I wasn't aware of mastery based testing, but now having read about it I see the issue of students gleaning off the best answers from the high performing students, altering them and passing them off as their own. Khan Academy uses this concept, but I feel that it works much better in cases of self-study and no-stakes grading. — Alan Whitteaker, Mar 26 '23 at 16:50
@allo There is still the problem that a student who starts learning from the pool a few days before the exam won't have enough time without having done exercises during the semester. I don't think much more can be done by you in this case. This simply boils down to the self-discipline of the student, and I feel you are doing your part in guiding them along the way. With respect to the feedback, you could keep an online feedback form open and continuously remind them to input their suggestions anonymously. Lastly, it may be helpful if you could show the students how to use GPT responsibly. — Alan Whitteaker, Mar 26 '23 at 16:58
The SE software is throwing a lot of flags here about there being too many comments.Because it seems that GPT and generative AI are of broader interest, I have also created a ChatGPT in Mathematics Education chatroom where we might be able to continue the discussion. — Xander Henderson, Mar 26 '23 at 17:22
@AlanWhitteaker Indeed. One never can prevent everything, but one can try to discourage the lazy way. — allo, Mar 26 '23 at 19:03

score 2 · Answer 11 · answered Mar 22 '23 at 17:09

Currently ChatGPT is very bad at citing and quoting sources.

This will probably change as the technology advances, but for now any question that asks to quote a source yields a real sounding but bogus answer.

Example:

How is the logarithm function extended to complex plane? Provide a quotation from a reliable source.

The logarithm function can be extended to the complex plane using complex analysis. One common way to define the complex logarithm function is through the complex exponential function:

"Given any nonzero complex number z, we define the complex exponential function as

e^z = e^(x+iy) = e^x * e^(iy) = e^x(cos y + i sin y)

where x and y are the real and imaginary parts of z, respectively. We can then define the complex logarithm function as the inverse of the complex exponential function. That is, if we define

w = ln z

then we have

e^w = z

for any nonzero complex number z."

This definition is from the book "Complex Variables and Applications" by James Ward Brown and Ruel V. Churchill, 9th edition, in Chapter 4, Section 4.4. The authors also note that there are some technical issues with this definition, such as the fact that the complex exponential function is periodic with period 2πi, which can affect the choice of branch of the complex logarithm function.

The source is relevant, but the correct chapter is 3 and the quoted text does not exist in the book.

Specialized LLMs are currently being developed specifically for this purpose and it would likely be completely solved in the next 1-2 years. I won't be surprised if GPT-5 can accomplish this perfectly. — JonathanReez, Mar 22 '23 at 21:52
You think it's viable for the instructor to cross-check all the student references? To the level of detail e.g. "source is relevant" but there's a made-up piece of text? Can you even prove that negative for every reference across an entire class? — Daniel R. Collins, Mar 23 '23 at 06:43
why would it need to be done for every reference? just do 1 in 10 and make the penalty for making stuff up very high. — George Savva, Mar 24 '23 at 09:26

Mahdi Majidi-Zolbanin · Answer 12 · 2023-03-27T15:30:24.180

1

(Edit: Here is another thought, different from my original response posted below: GPT at its current stage of development is pretty bad in solving mathematics problems, as demonstrated by examples posted below and many other examples that I did not post here. It needs further development. But, assuming that it improves, at some point in the future we will see the possibility of administering homework and exams on GPT itself, in such a way that GPT is the proctor and if a student tries to ask GPT to solve a problem that is a homework or exam problem, GPT will be able to recognize that and will remind the student that this is his homework or exam and must be solved by the student.)

Here are a number of examples of Calculus problems that ChatGPT was not able to solve satisfactorily (at least now, but it may learn!)

Example 1) (Use large numbers) Explain how you would integrate $\int\sin^{679}(x) dx$, but don't find the answer.

The successful solution by a student is to separate one $\sin(x)$, then write the remaining $\sin^{678}(x)$ as $(\sin^2(x))^{339}$, which is equal to $(1-\cos^2(x))^{339}$ and then say use the substitution $u=\cos(x)$, although the answer to that integral will be very complicated and long.

Here is ChatGPT's response to the same question:

Example 2) Suppose the series $\sum_{n=1}^\infty a_n^2$ is convergent. What can we say about the convergence or divergence of the series $\sum_{n=1}^\infty \frac{a_n^2}{n}$?

The successful solution by a student will use the Comparison Test, as $0\leq \frac{a_n^2}{n}\leq a_n^2$ and conclude that the series $\sum_{n=1}^\infty\frac{a_n^2}{n}$ is convergent.

Here is ChatGPT's response to the same question (note that the conclusion is correct but the reasoning doesn't make sense):

Example 3) (Include extraneous information) Suppose $f$ is a continuous function and $g(x)=\int_1^x f(t)dt$. If $f(4)=0$ and $f(5)=1$ can we find a critical number of $g(x)$?

The successful solution by a student is to say since $f$ is continuous, $g$ is differentiable and $g^\prime(x)=f(x)$. Since $g^\prime(4)=f(4)=0$, $x=4$ is a critical number of $g$. That $f(5)=1$ is irrelevant.

Here is ChatGPT's response to the same question, which does not make sense:

Example 4) suppose $f(x) = x+3$ when $x\leq-2$, and $f(x) = -x/2$ when $-2<x<2$ and $f(x) = x-3$ when $x\geq2$. Suppose $g(x)=\int_{-4}^x f(t)dt$. Can we find the extreme values of $g$ on the interval $[-4,6]$?

The successful solution by a student would use the Closed Interval Method. As $f$ is continuous, $g^\prime(x)=f(x)$ and $g$ has critical numbers at $x=-3,0,3$. To find the extreme values of $g$ on the interval $[-4,6]$ it suffices to find and compare the values of $g(-4), g(-3), g(0), g(3)$ and $g(6)$.

Here is ChatGPT's response to the same question, which doesn't make sense (it actually got stuck for more than 5 minutes there):

Since ChatGPT got stuck in the middle of solving this problem, I stopped it and asked it to regenerate its response. In its new response, somewhere it said that $-3$ is not in the interval $[-4,6]$! So I challenged it and here is the conversation that followed:

Note that it is still saying $-3$ is not in the open interval $(-4,6)$!

Example 5) Is it possible to integrate $\frac{x}{\sqrt{9-x^2}}$ using integration by parts?

ChatGPT got stuck again in the middle of solving the problem:

Example 6) Here is an elementary question: Can a rectangle and a circle have the same area?

Here is ChatGPT's response:

edited Mar 27 '23 at 15:30

answered Mar 23 '23 at 00:35

Mahdi Majidi-Zolbanin

1,102
4
17

3

You should try it with the new WolframAlpha plugin: https://writings.stephenwolfram.com/2023/03/chatgpt-gets-its-wolfram-superpowers/ (once it’s released to the general public) – JonathanReez Mar 24 '23 at 14:12
@JonathanReez I don't think WolframAlpha plugin can help with Example 6. Sure, if you ask ChatGPT to revise its answer it may be able to correct it, but to do that, one has to know the correct answer, to begin with. – Mahdi Majidi-Zolbanin Mar 24 '23 at 19:31
For the last one, GPT-4 says: Yes, a rectangle and a circle can have the same area. <...> To find a rectangle and a circle with the same area, you can simply choose the dimensions of a rectangle and then solve for the radius of the circle that would result in the same area. <...>. So your last example needs an update for GPT-4 or can be removed. – JonathanReez Mar 24 '23 at 19:54
2

@JonathanReez Are you suggesting that I should find a question that GPT-4 cannot answer correctly? Well, then GPT-5 will answer it correctly. The point I am making is that for every value of n, one can find questions that GPT-n cannot answer correctly. Now, if a student doesn't know the correct answer to a question and asks GPT-n, then how is the student supposed to know whether the answer given by GPT-n is correct or not? – Mahdi Majidi-Zolbanin Mar 24 '23 at 20:11
You are right - GPT-n might be able to solve any problem GPT-4 fails at today. But this also means that finding such homework problems will become increasingly hard and thus such advice is quite short lived. – JonathanReez Mar 24 '23 at 20:19
@JonathanReez Yes, I agree with you, it will become increasingly difficult to find homework problems that AI cannot solve. But the question will remain: how do we ever know the answer given by AI is correct? – Mahdi Majidi-Zolbanin Mar 24 '23 at 20:25
How do we know the answer given by the teacher is correct? :-) it’s an unsolvable problem in the end. – JonathanReez Mar 24 '23 at 20:43
I have downvoted this answer, because I don't think it really addresses the question being asked. Your answer seems to reduce to "ask questions which you know that GPT can't answer". But, as I pointed out in my answer, generative AI is only going to get better. Trying to ask questions which cannot be answered by generative AI is a losing battle. This is not a sustainable approach to the problem (if one views it as a problem). – Xander Henderson Mar 26 '23 at 17:13
Indeed, I just asked if a circle and a rectangle could have the same area. The response is now "Yes, if the rectangle is a square with side length $\sqrt{\pi}r$." Give it time, and I am sure that it will give a better answer. – Xander Henderson Mar 26 '23 at 17:18
@XanderHenderson Thanks for your comment. Last night it could not answer correctly whether a triangle and a circle can have the same areas. I tried to teach it and gave an example. Then I asked if it learned it. It said yes, it had "updated its knowledge based on analyzing the new information". I asked the same question after 10 minutes again, but it gave me the wrong answer! But when I asked the same question today, it gave me the correct answer. There are two possibilities: either GPT can really learn (although updating its knowledge is not immediate) or because of a degree of randomness – Mahdi Majidi-Zolbanin Mar 26 '23 at 18:37
in its algorithm, sometimes it gives a correct answer and sometimes it doesn't. But another implication of my answer is this: for what value of n should we start trusting the answers that GPT-n gives us? I have given many examples of incorrect answers by ChatGPT. Of course these are questions that we know the answer to. But what if we don't know the answer to a question and we ask GPT-n? Are we going to believe the answer it gives? What it the criteria for truth here? I can always find questions that GPT-n cannot answer correctly. Or can't I? How do we know I can't? – Mahdi Majidi-Zolbanin Mar 26 '23 at 18:41
@MahdiMajidi-Zolbanin The point is not that ChatGPT has or has not learned the answer to a particular question. The point is that generative AI is a rapidly evolving field. Any strategy which relies on what it cannot do today is doomed to failure, as we don't know what it might be able to do tomorrow. – Xander Henderson Mar 26 '23 at 20:14
@XanderHenderson "The point is that generative AI is a rapidly evolving field. Any strategy which relies on what it cannot do today is doomed to failure, as we don't know what it might be able to do tomorrow." I do not disagree with that. But that's not news to me. We could make the same statement twenty years ago. What we see today, is pretty bad. In fact very bad. It is so bad that it cannot tell 2 and $\pi$ are not equal, before stating that they are equal. Let me know if you want screenshots to believe me. Yes, we have known for decades that one day AI will take over, but this isn't that – Mahdi Majidi-Zolbanin Mar 26 '23 at 22:45
How is your answer responsive to the question "What should be done about ChatGPT in the learning environment?" – Xander Henderson Mar 27 '23 at 12:46
2

@XanderHenderson My answer is saying: don't worry about ChatGPT, it is so bad that, if you give a bunch of random exercises to your students and tell them they have the option to use ChatGPT, those who don't use it will do a better job than those who copy ChatGPT's answers. I was actually more impressed by ChatGPT when I posted my answer, compared to now. But the more I tried it, the more I realized how bad it was. – Mahdi Majidi-Zolbanin Mar 27 '23 at 15:02

score 1 · Answer 13 · answered Mar 23 '23 at 22:36

Enlist the Enemy

Ask ChatGPT to help you create math exercises that deter cheating with ChatGPT. No idea if this will produce any interesting results, but it seems like this kind of path is the only way to keep up with these systems. Make them an ally instead of an enemy.

Create a HoneyPot

Insert unsolvable problems into the homework. Inform the students that sometimes they will encounter a problem that is unsolvable, and if they do, their answer should be "unsolvable", and ideally, an informal explanation about where the problem is. This is, fortunately, ChatGPT's weakness. It doesn't know truth. It's much better at producing an answer than actually evaluating it. When students "solve" all the unsolvable problems, with very convincing looking answers, then you know they are cheating with AI.

This does make homework more difficult, because now students must determine whether a given problem is actually solvable. If a student asks ChatGPT whether an answer is solvable, the AI may give them either answer, and justify it fully. Some students may erroneously identify an unsolvable problem in the same way that ChatGPT does, and that is a problem. It's not a foolproof technique. But it would be interesting to see if it effectively separates cheaters from learners.

Critiquing Exercises

Ask ChatGPT to solve several exercise problems. Keep asking so that you get a set of correct and incorrect solutions. Favor the question where the AI is equally likely to give you a correct vs. incorrect answer, or is biased towards incorrectness (probably most of them, if I had to guess). Make the student exercise to read the problem and ChatGPT's answer and verify that it's correct or point out the invalid leap(s) of logic that it makes.

This goes back to the fact that ChatGPT is very good at generating answers, but not so good at telling you which ones actually correspond to reality. So test the students on their ability to do so.

In the same vein, pick exercises as above, but only give half of the AI's answer and ask the students to complete it. Again, include both true and false starts so that the students have to evaluate whether the solution they are given is even headed in the right direction. As long as ChatGPT is happy to complete these solutions with wrong answers as often as right ones, it should be easier to discriminate the cheating students from the learners.

Conclusion

When I look into my crystal ball, I see "overseeing the AI" as the future job of most humans. That is, humans have used dogs to help them hunt for thousands of years. They've used shovels to help them dig. And radar to see things far away, through walls, or even underground. But at the end of the day, humans harvest the prey, collect the ore, and evaluate the image. The tools simply do the dirty work.

A lot of knowledge work involves searching the space of ideas and making bets on which paths are most fruitful. I don't think AI is going to replace humans in this activity. Rather, I think they will more likely do the grunt work spawning raw ideas, mechanically checking arguments, and the like. I predict that humans will use their judgment to connect ideas from related fields, guide the raw efforts of the AI, and refine the results.

If I'm right, then this whole "bring the AI on board and teach kids to evaluate and harness it" will be a skill set they will use extensively by the time they are well into their careers. And yes, it is just as important to teach kids to be skeptical of the answers they get as it is to teach them to use it. And hopefully, that will make all of us better thinkers and filters of misinformation. To this extent, AI may help us to mature as a society.

Creating Exercises) I have looked at it and we may add some. But many contain subtle errors, so it is better to provide ideas than to write the exercises. Honeypot) I don't want to make life difficult for the students. I want them to pass, and in order to pass I want them to learn. It's not about whether we catch them cheating, but we don't want them cheating in the first place. Critiquing) This isn't suitable for most (of our) maths exercises. Conclusion) This may happen, but the basic math courses will still be required, just as you still learn to multiply without a calculator. — allo, Mar 24 '23 at 12:01
https://writings.stephenwolfram.com/2023/03/chatgpt-gets-its-wolfram-superpowers/ - it got an integration with WolframAlpha today making it much more powerful. Any hot takes about how AI cannot do X tend to age very, very poorly these days. — JonathanReez, Mar 24 '23 at 14:15
@JonathanReez on the contrary...ChatGPT isn't doing math, WolframAlpha is. The job of ChatGPT will be to translate whatever natural language question is posed to it, and this is where we will see how good it is. WolframAlpha itself also does a fair bit of interpreting the intention of the user, so ChatGPT only has to get "close". Now, if someone makes a Deep Learning network that replaces WolframAlpha, a la AlphaZero, we will be having an entirely different discussion that will end up with humans mathematicians becoming obsolete. — Lawnmower Man, Mar 24 '23 at 22:07
ChatGPT now got plugins and can use, for example, WolframAlpha. This will make things more powerful and avoid the need for a language model to learn math that specialized systems can do better. And it will affect what kind of solutions ChatGPT can provide to solve exercises. — allo, Mar 27 '23 at 14:22

NotThatGuy · Answer 14 · 2023-03-24T14:41:57.603

You may be trying to band-aid a missing leg.

As another answer mentions, the internet provides a number of means to easily cheat fairly easily. You can take some measures to stop obvious cases of cheating (and you should take some such measures), but there's only so much you can do.

As fedja puts it, the job of teachers is "to provide an opportunity to learn to everybody who is willing to learn".

My conclusion is slightly different, however: you shouldn't necessarily based grades (almost) fully on proctored exams. A student can have a moderately decent understanding of a topic and still not perform all that well in an exam due to the time constraint, due to stress, due to not having memorised the appropriate formulas, because they were having a bad day or week, etc.

If it weren't for the possibility of cheating, I'd say the best grading scheme is likely mostly one without exams (doctors, for example, probably still need surgical exams). There are also measures to focus on testing whether students actually understand the material rather than testing whether they were able to e.g. memorise a bunch of things that they can recall within a short timeframe, and that they can write quickly enough, but I won't go into that here.

For different courses (even within maths), it may be more or less easy to cheat on homework (with ChatGBT or through other means).

My suggestion is to possibly reduce the weight of homework so having a degree continues to actually mean something for what you know (even if it already often means very little). But also don't go to to extreme measures to avoid having someone pass mostly through cheating: if a student cheats, they're shooting themselves in the foot by squandering what's hopefully a good opportunity for them to learn things they'll use later in life. Don't then shoot other students in the foot to put them on equal footing with the cheater.

I can't, however, tell you how exactly you should weight homework, quizzes, bigger tests, projects and exams to come up with a final grade. That's something you'll need to figure out based on all the factors involved.

One option to consider is to have an overall grade that's calculated in some way (which has a minimal passing grade), but then to also have a minimal grade for the exam only, which is lower than the overall passing grade.

Or one could combine homework, etc. with exams in some variable way. You could, for example, say that the maximum distance between the two is 20%, and the exam mark will drag the homework mark down, or raise it up, if the distance exceeds 20%. The downside here would be that the grading would be less obvious to students (even if you're transparent about how it's weighted, which you should be), and this may make it feel unfair.