9

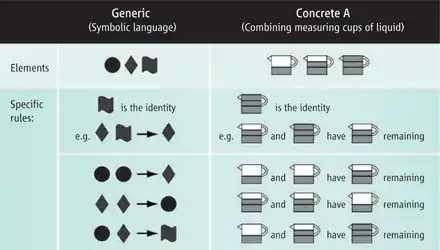
In my own personal experience in teaching linear algebra, where many students encounter abstract ideas for the first time, I find that most students have trouble consolidating observations from concrete examples into understanding of abstract ideas.

Very often, after giving many examples, students understood the examples very well, but they can't say anything beyond that.

Take the concept of subspace, for example: Many students can know 5 examples of subspaces of vector spaces very well, yet cannot answer the most basic question about any subspace they have not studied. E.g., "if we have a set of functions in the vector space of continuous functions over [a,b], how can we check if this set form a subspace?"

I wonder if this a common problem: Are any empirical studies or observations derived from large samples on how well average undergraduate students can learn abstract concepts through concrete examples.

Bilbo
  • 271
  • 2
  • 3
  • 5
    I would love to see empirical studies on this phenomenon. My experience suggests there is some significant portion of humans who cannot understand abstract concepts at all, or who cannot relate an abstract concept to a concrete example. Then again, there are levels of mathematical abstraction (e.g. perverse sheaves) I cannot understand. – Alexander Woo Apr 27 '22 at 16:54
  • 5
    This is probably a matter of practice, time, and effort. If this is their first time using an abstract definition like "subspace," is it at all surprising that they students don't immediately get it? Even the idea that "knowing the definitions in mathematics is extremely important" is novel. Since you cannot know whether or not everyone is capable of such abstract thinking, I recommend that everyone is capable of it, and think hard about what you can do to help students navigate abstract mathematical definitions. – David Steinberg Apr 27 '22 at 17:23
  • 4
    Just some extensive anecdotal info: it does seem to take time and effort for people to see the commonality among (even adroitly-chosen) examples. AND this way of learning is an extreme novelty for many, who then seem not to know that "action is required". Yes, I myself see "definitions" as simply optimally interpolating "sufficiently many good examples", but this is a viewpoint that does not occur toooo often in popular discourse. – paul garrett Apr 27 '22 at 17:49
  • 3
    @DavidSteinberg: What many people don't realize is that there is a price to such positive thinking. If you believe all your students are capable of it with the right instruction, and you try your best but still find students who are not capable of it, you might think you are a failure as a teacher and quit or, if you are prone to certain forms of depression, worse. – Alexander Woo Apr 27 '22 at 18:00
  • 5
    @AlexanderWoo What we can do instead is to say "I am not sure whether this particular student has this capability, but we can both try and devote our best effort to it. Whether or not we 'succeed' the effort is likely to lead to positive growth.". I do mourn that our educational system is set up to have "success" and "failure" instead of celebrating creativity, joy, growth, persistence, etc. – Steven Gubkin Apr 27 '22 at 18:35
  • 2
    In some other contexts, concrete examples are exactly the thing that enables them to understand abstract concepts. But I suspect some of your students are not there to learn abstract concepts; they're there in order to try to earn a grade by obeying the instructor. – Michael Hardy Apr 28 '22 at 03:18
  • @MichaelHardy, "concrete examples are exactly the thing that enables them to understand abstract concepts" -- Is that true? That's my main question. I always assumed that that is true, or at least I hope that's true. I have seen very little evidence. Sure, there are students whose only goal is do or pretend to do whatever to pass. But I'm not thinking of them here. For those who genuinely want to understand abstract concepts, does concrete examples do what we think they do? – Bilbo Apr 28 '22 at 18:57
  • @Bilbo : I said "In some other contexts". – Michael Hardy Apr 29 '22 at 19:47
  • @Bilbo : Consider Euclid's argument for the infinitude of primes. If $S$ is any finite set of primes then the prime factors of $1+\prod S$ are not members of $S;$ thus $S$ can always be extended to a larger set of primes. Many students dutifully listen to this and ask no questions, but then later you call their attention to the sequence $\ldots,140,141,142,143,144,145,146,\ldots$ and say that since $143$ is divisible by $11,$ you're not due for another multiple of $11$ until you get up to $143+11,$ or down to $143-11,$ and that is the first time that they understand the proof. $\qquad$ – Michael Hardy Apr 29 '22 at 19:54
  • 3
    @Bilbo : And that is an example of the fact that many students who superficially appear adept in elementary algebra often fail to understand elementary proofs relying on algebra. They haven't connected the abstract with concrete examples. A really simple example is the student who knows very well that $x^2-y^2 = (x-y)(x+y)$ but doesn't know what you're talking about if you say that tells them how to factor $899$ since $899$ is $1$ less than $30^2. \qquad$ – Michael Hardy Apr 29 '22 at 20:01

1 Answers1

9

The following article in Science has now been cited 388 times according to Google Scholar. I am not in a position to assess this paper or to characterize all the subsequent discussion, but it seems quite relevant to the OP's question.

Kaminsky, J.A., Sloutsky, V.M., & Heckler, A.F. The advantage of abstract examples in learning math. Science, 320, no. 5875 (2008): 454-455. DOI.

"Undergraduate students may benefit more from learning mathematics through a single abstract, symbolic representation than from learning multiple concrete examples."

"What we are suggesting is that grounding mathematics deeply in concrete contexts can potentially limit its applicability. Students might be better able to generalize mathematical concepts to various situations if the concepts have been introduced with the use of generic instantiations."

figure

Joseph O'Rourke
  • 29,827
  • 6
  • 61
  • 140
  • 3
    Wow. Quite amazing, actually. Such a general learning approach may be very different from a significant fraction (not at all "all") of professional mathematicians. – paul garrett Apr 27 '22 at 23:17
  • 4
    Different people learn differently. Some (including me) want a definition first, then go invent some examples , and then ask you for more examples if the invented ones are too special. Others would rather begin with examples, then go invent a definition to cover them, and then ask you for more examples if their definition isn't what you had in mind. – Andreas Blass Apr 28 '22 at 00:38
  • 1
    @AndreasBlass, I suspect the two kinds of people you described are a tiny minority of the students (but likely over-represented on this site). – Bilbo Apr 28 '22 at 19:01