Use of language: "perfect square". is this useful or a hindrance?

Question

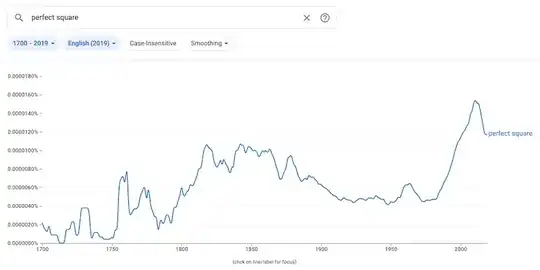
I have recently been noticing the tendency to use the term "perfect square" when "square number" is really what is meant.

Usually I have seen it at elementary level: introductory algebra, popular puzzle pages, and so on.

I confess I cringe at the term. There are already several usages in various branches of mathematics of the descriptor "perfect", and applying it to the term "square" does not seem to be to be a useful one. For a start, it can confuse a bright but naïve student into wondering what such a square has to do with "perfect numbers", and whether a "perfect square" means a "square number which happens also to be a perfect number" (and then go running off vainly to find one).

Are there any advantages to the term "perfect square", or is it just to impress upon the student the gosh-wowery of a concept which is really pretty mundane? If you're in the realm of integers (sorry, we're at an elementary level here, "counting numbers"), then your number is going to be either "square" or it isn't. There's no such thing as an "imperfect square", and while I will grant you that $143$, for example, is "almost square", it's not square.

But I keep seeing it on the Mathematics forum, for no perceptibly useful effect.

Any professional educators out there who find that expressing it as a "perfect square" aids understanding and doesn't hinder the learning process?

The only advantage I can think of is that it is established. Do you have any evidence that this causes confusion? — David Steinberg, Mar 07 '22 at 18:51
I suspect your phrase usage issue is more regional than temporal. For what it's worth, "perfect square" is pretty much all I ever heard through high school and college (1970s), so this usage is certainly not recent, at least not in many places in the U.S. In fact, I'm not sure I ever heard the phrase "square number" back then (and probably almost never even now), although because its meaning would have been obvious to me, I probably didn't pay attention if I did hear it. — Dave L Renfro, Mar 07 '22 at 19:18
This google-books search, restricted to the 1800s clearly shows that the phrase "perfect square" is not something all that new under the sun. I realize that many of these uses refer to algebraic perfect squares, but there are also plenty of numerical uses of this term among those 1800s google hits. — Dave L Renfro, Mar 07 '22 at 19:21
@MatthewDaly I tried to upgrade your comment into an answer. :P — Chris Cunningham, Mar 07 '22 at 19:38
The correct description is "a square in the ring ${\bf Z}[x]$." But this it too technical. So "perfect square" is what people have used for many years. Can you offer an alternative? — user52817, Mar 07 '22 at 19:48
@MatthewDaly I seem to have failed to do so. Someone should write the answer that OP wants, based on Matthew's observation. — Chris Cunningham, Mar 07 '22 at 20:53
@user52817 Good point! Although I'm not sure if this is the usage the OP had in mind, it's a good example of an intuitive notion which could be hard to define explicitly for younger students. — Michał Miśkiewicz, Mar 08 '22 at 10:42
In high school I attended a summer mathematics program where I did a project on perfect numbers. It never occurred to me that these numbers would be associated with perfect squares. Nor did it confuse the other high school students that I presented to. I don't think confusion is an issue. — Amy B, Mar 08 '22 at 18:06

score 13 · Answer 1 · answered Mar 07 '22 at 19:38

13

Suppose the term "perfect square" was not in use.

Then when I asked you if

$x^2 + 6x +7$

was a square, you could conceivably say "sure, everything is a square:"

$\sqrt{x^2 + 6x + 7}^2 = x^2 + 6x + 7$.

So I would need to clarify and invent new terminology. I would have to say that $x^2 + 6x + 9$ is a "good square" as opposed to $x^2 + 6x + 7$ which is admittedly a "square." "Perfect square" seems like a fine choice for that term, because it correctly indicates that there is somehow a unique choice in some circumstances.

Something like "polynomial square" might be more modern or precise wording, but your question is why we need a second word at all, and this is a good reason.

answered Mar 07 '22 at 19:38

Chris Cunningham

21,474
6
63
148

3

Well yes, but we're not talking about polynomials, we're talking about integers. – Prime Mover Mar 07 '22 at 20:14
1

Seems I didn't communicate well. I'll leave this one though. – Chris Cunningham Mar 07 '22 at 20:52
What I mean is, while there is a case for using it in this context, for a polynomial (although I have not actually heard of it used this way), I am not sure it justifies using it in the context of integers. – Prime Mover Mar 07 '22 at 20:59
6

Is it possible to create an even simpler example like this. 36 is a perfect square (of the number 6). 20.25 is a square (of 4.5); but it's not a perfect square, since 20.25 is not an integer. Does that example work too? – stevec Mar 08 '22 at 03:51
5

@PrimeMover or another example: 36 is a perfect square, since it's the square of an integer, but 20 isn't, since the square root of 20 isn't an integer. How does one distinguish between 36 and 20 in this case? – muru Mar 08 '22 at 10:29
@muru $36$ is a square number, $20$ is not a square number. Where's the confusion? – Prime Mover Mar 08 '22 at 18:42
$20.25$ is the square of a rational number but its not a square number. It's the quotient of one square by another. Dividing a square number by another square number does not mean its quotient is square. – Prime Mover Mar 08 '22 at 18:56
5

@PrimeMover I guess then the confusion is that I as a student would prefer to not be lied to, and then told at a later stage, "Remember when I said 20 wasn't a square? Well, it is now." That has happened once too often, and my favourite mathematics teachers have been the ones who freely admit that my questions do have valid answers and will be covered at a later stage (and even on occasion letting me know of these future concepts so I can look them up myself if want to). Patience while learning is also something that must be taught to many people. – muru Mar 08 '22 at 20:12
@muru Sorry but just because $20 = \sqrt{20}^2$ does not make $20$ a square. So whatever your teachers were telling you, they were not doing a very good job. – Prime Mover Mar 08 '22 at 20:15
2

@PrimeMover as for both of those sentences, I and several others will disagree with you. I have nothing more to say to people who bring personal attacks into such discussions. – muru Mar 08 '22 at 20:23
4

@PrimeMover: Of course 20 is a square. Draw a square $\sqrt{20}$ inches on each side and measure its area. It's not a perfect square, I think you are trying to say. – Nick Matteo Mar 08 '22 at 20:31
1

@stevec: I've seen that included in the definition of a perfect square. E.g., Martin-Gay, Prealgebra & Introductory Algebra, Sec. 7.3: "Numbers like $\frac 1 4$, 36, $\frac 4 {25}$, and 1 are called perfect squares because their square root is a whole number or a fraction." – Daniel R. Collins Mar 09 '22 at 00:10
1

@DanielR.Collins ... which would be entirely consistent with (what I claim is) the definition of a perfect square, i.e. an element of a ring which has a square root in that ring. $4/25$ has a square root in $\mathbb{Q}$. – Xander Henderson Mar 09 '22 at 00:17
2

Would you argue that we need the term "perfect prime", because 2.3 isn't divisible by any integer? – Kaz Mar 10 '22 at 01:47
@Kaz I like this objection. I don't think it is a problem though. I would say that I will only ask you whether natural numbers are prime. It's not possible to avoid the "square / perfect square" issue in the same way. – Chris Cunningham Mar 10 '22 at 19:10
@ChrisCunningham Yes it is; it is only meaningful to ask whether an integer is a perfect square. Or even, or odd for that matter. A non-integer is vacuously not a perfect square. Perfect squareness has a direct connection to primeness because it has to do with factoring. A perfect square is necessarily a composite, which has even number of factors, each of which has even duplicity. (Therefore those factors can be split into two identical groups, the product of which is the integer.) E.g. 900 is a perfect square because it's 2x2x3x3x5x5, which regroups as 2x3x5 x 2x3x5 = 30 x 30. – Kaz Mar 11 '22 at 00:15

Xander Henderson · Answer 2 · 2022-03-11T00:43:46.387

According to this Google ngram, the term "perfect square" has been in use since at least the 18th century (there are earlier uses, but the ngram viewer reports usage as a percentage of words in the corpus, and I suspect that the smaller number of published works predating the 18th century distort things).

It is worth emphasizing that "perfect square" is a set phrase. Like many set phrases (which occur in most languages), the phrase should not be parsed individually, but should be interpreted as a single, indivisible unit of syntax.^[1] The phrase does not imply that there are some squares which are perfect, and others which are not—the phrase should not—and cannot—be parsed in this way.

A discussion of why this term developed, and whether or not it is distinguished from the notion of a "square" or "square number" is likely off-topic here, and is something that I lack the expertise to answer, anyway (you might try asking on History of Science & Math).

However, as a pedagogical concern, the term "perfect square" is perfectly correct idiomatic mathematical English. Indeed, I disagree with your premise that the term is "imprecise and woolly".^[2] It is a well-understood term which, in most contexts, means "a ring element $x$ such that there exists some ring element $a$ such that $a^2 = x$" (that is, a perfect square is an element of a ring which has a square root in that ring).

Because this phrase is used and understood by mathematicians, and because part of the job of a mathematics educator is to teach students the language used by working mathematicians, it is appropriate to teach students the phrase. As a matter of opinion, I don't think that you do any lasting harm by avoiding the term and using "square number" (or "square integer") instead, but I'm not sure that you are doing any good, either.

[1] For example:

"to kick the bucket" means to die—it has nothing to do with actually kicking a literal bucket;
when one is "under the weather", it means that one is not feeling well—again, a literal parsing is nonsense; and
to apply "elbow grease" to a problem means to solve that problem with (possibly difficult) manual labor.

None of these phrases make much sense if you try to parse them word-by-word, but they have set meanings in the English language. Such phrasemes are common in human languages, including mathematical language.

[2] If you would like to target your ire at a poorly defined, wooly, imprecise term which is commonly used in mathematics, I would suggest that you turn your eye toward the word "fractal".

@usul 143 is a perfect square in the ring $\mathbb R$, which is not particularly exciting because that is true of every nonnegative element of $\mathbb R$. It is not a perfect square in $\mathbb Z$, where the concept of a perfect square is less trivial and more interesting. — J. Murray, Mar 08 '22 at 07:07
@usul In what ring? In $\mathbb{Z}$, no. In $\mathbb{R}$ or $\mathbb{C}$, yes. Though any nonnegative real number is a perfect square in $\mathbb{R}$, and anything at all is a perfect square in $\mathbb{C}$, so the concept of a perfect square is less useful in those rings. — Xander Henderson, Mar 08 '22 at 11:14
I think the discussion needed to answer my question shows that the term is pedagogically problematic and the question has a valid point. I wouldn't want to explain the difference between perfect square relative to $\mathbb{N}$ versus $\mathbb{Q}$ to an elementary student. Nor would I want to teach terms where students and I have to clarify the relevant ring every time they use them. — usul, Mar 08 '22 at 19:21
@usul Nowhere did I suggest that an instructor of third graders should introduce rings. But I still think that it is important to teach students the language which is used in mathematics. "Perfect square" is a set phrase, which is used. To a third grader, I would probably say "A perfect square is a whole number which is the square of a whole number. For example, $9 = 3 \times 3$. When you get older, you might see other examples of perfect squares which are not whole numbers." — Xander Henderson, Mar 10 '22 at 11:32
It is no different from telling a kindergartener that "We don't know how to subtract five from three yet," or a middle schooler that "the square root of negative one is not defined (yet)." Teach the language, but do it in an age appropriate way. — Xander Henderson, Mar 10 '22 at 11:33
It's definitely different in my opinion -- it's easy to explain "we don't know how to do this yet", but harder to explain that 5 is not a perfect square right now, but later it might be. — usul, Mar 10 '22 at 18:10
@usul You are certainly entitled to your opinion, but I really don't think that it is any worse than avoiding negative numbers in kindergarten, or complex numbers in fourth grade. — Xander Henderson, Mar 11 '22 at 00:48

ryang · Answer 3 · 2022-03-08T05:04:28.447

5

perfect square
absolutely perfect
utterly exhausted
pretty ridiculous
quite certain

In each phrase above, the modifier is added for emphasis rather than to indicate gradation/degree.

Just as "perfect square" isn't meant to suggest that an imperfect square is a thing, "absolutely perfect" isn't intended to contrast with "partially perfect".

These examples are of idiomatic English as used by fluent speakers/writers. (In fact, grammarians call “exhausted” an extreme, ungraded adjective for the reason just highlighted.)

Although natural language is not a logical language even in mathematics—where context continues to implicitly guide usage and interpretation—it rightly pervades communication in mathematics.

The salient point is that there’s a difference between inaccurate language that reflects careless thinking, and standard terms that aren’t epitomes of systematic design.

P.S. Weaved in my comments that were previously below.

edited Mar 08 '22 at 05:04

answered Mar 07 '22 at 17:34

ryang

1,822
13
19

1

Therefore mathematics teachers are able to get away with appallingly imprecise and woolly language just because muggles do? When they're supposed to be teaching the subject? I confess I am not party to that viewpoint. – Prime Mover Mar 07 '22 at 20:15
I don't care about "fluent speakers / writers" if they're mathematical illiterates. What is important is the communication of mathematical ideas accurately and succinctly, not in wowing intellectual children with fairy stories and political propaganda. – Prime Mover Mar 07 '22 at 22:53
9

@PrimeMover "Perfect square" is an idiomatic mathematical expression. It has a definition in mathematics (generally speaking, an element of a ring which has a square root in that ring), and is widely understood by practitioners of mathematics. You should not think of it as an [adjective] [noun] phrase, but as a single, indivisible term. – Xander Henderson Mar 07 '22 at 22:59
9

"wowing intellectual children with fairy stories and political propaganda" - um, that escalated quickly. – Michael MacAskill Mar 08 '22 at 04:11
(To me hearing) "quite certain" and "pretty sure" reduce emphasis whereas "pretty ridiculous" increases it. ie "I am certain" is stronger than "I am quite certain" – Rusi Mar 08 '22 at 08:15
1

The word "quite" has two meanings. It can either be used as an intensifier or as a mollifier. In American English, it is typically used to intensify ("quite certain" means "very certain", i.e. more certain than just "certain"), whereas in British English, it tends to be used as a mollifier ("quite certain" means "fairly certain", i.e. less certain than "certain"). The US and UK: two peoples, separated by a common language. – Xander Henderson Mar 08 '22 at 11:25
@Rusi I know how you mean. But the modifier adverbs in the collocations "quite certain" and "quite sure", when uttered by native speakers, do indeed serve as emphasis rather than indicators of degree/extent. In any case, this discussion is akin to saying that calling Brownie, who is a white dog, by its name is bad practice. – ryang Mar 08 '22 at 11:50
@XanderHenderson While "quite" indeed has two contrasting meanings, the meaning 'quite=completely' in "quite certain" and "quite sure" in fact sounds particularly British to my ear; on the other hand, "I'm quite tired" (as opposed to "I'm quite exhausted") of course has the opposite meaning 'quite=to a fair extent'. I don't think the idiomatic distinction between these two meanings of 'quite' is a distinguishing feature of AmE versus BrE. – ryang Mar 08 '22 at 11:59
1

@ryang Interesting. I only learned about the distinction between the two uses of "quite" recently (though a [ell.se] post, I think). The poster argued as I did above, and that fit well with my own (American) experience. https://ell.stackexchange.com/a/24106 – Xander Henderson Mar 08 '22 at 12:07
1

@ryang I am simply reporting what someone else said---to my ear "quite" is always an intensifier (except when uttered by Alfred Pennyworth to Bruce Wayne, in which case it seems to represent a statement of tired resignation---it has to be the accent). But this maybe isn't the place for this discussion. I guess the point is that "quite" is not necessarily an intensifier. :D – Xander Henderson Mar 08 '22 at 12:47

score 5 · Answer 4 · answered Mar 08 '22 at 01:39

5

@PrimeMover, I guess the content of whatever terminology would be good here is that we mean "square of an integer". "Square integer" is ambiguous, because, well, every integer is the square of a complex number, and complex numbers are standard. Positive integers are squares of real numbers, which are even more standard.

So, seriously, how to distinguish? Partly by tradition, yes, the phrase "perfect square" has established itself as meaning "square of an integer". It is a partly artifactual, but useful, terminology. And, at worst, harmless, so, what's any serious objection to it? It (in practice) removes ambiguity, unlike simply "square"... ("square of what?").

Yes, one might declare that in certain highly controlled contexts there'd be no ambiguity, but, actually, mathematical contexts are not sufficiently centrally controlled so as to avoid this kind of thing. :)

answered Mar 08 '22 at 01:39

paul garrett

14,597
2
33
71

Yes of course every integer is the square of some number, whether integer, real or complex. Hence, oh never mind. – Prime Mover Mar 08 '22 at 06:01
2

@PrimeMover I don't understand this comment; are you saying that 8 and 9 are both exactly as square as each other, and so distinguishing between them is unimportant? – Chris Cunningham Mar 08 '22 at 14:50
@ChrisCunningham No, I'm saying it's utterly pointless to call $8$ a square because, on the logic that everything is a square of something, even $-\pi$ is the square of $i \sqrt \pi$, referring to any such number as a "square" means that the term is meaningless to the point of comedy. Since it makes sense to refer to a number as "square" in order to distinguish it from a number which is "not square", it makes utterly no sense at all to add "perfect" in front of it, like a 6-year-old who says "I'm really telling the truth." Sorry, thought was too obvious to continue the thought. – Prime Mover Mar 08 '22 at 18:46
Certainly it'd be "inefficient" to say that an integer was "a square", if it were not a square of an integer, because "everything is the square of something". Still, kids (most people) do not think that way. It's more solid communication to have redundance, rather than depending on "type-checking" or other "logical" principles for kids/people to understand things. "The logic of semantics" is not what moves or explains-to people. It took me a few decades, as a college math teacher, to catch on, I admit. I was infatuated with some idea that people should think a certain artificial way... :) – paul garrett Mar 09 '22 at 04:27

Rusi · Answer 5 · 2022-03-08T14:19:42.587

0

I've some ideological sympathy with the question.

If OTOH you want a hand in changing hundreds of years of tradition,... er... sorry I've not the musculature for that exercise .

Here are some similar inapt adjectives that have annoyed me and slowed my students in my 3+ decades of teaching discrete math.

Many-One/One-Many Relation

A relation $R : A \leftrightarrow B$ has property $P$ defined by: $$\forall x \in A,~ y_1, y_2 \in B: xRy_1 \land xRy_2 \Rightarrow y_1 = y_2$$

Decoded this means that there are not two different $y_1, y_2$s for any one $x$; ie there is no fan-out from $A$ to $B$.

In an ideal world $P$ would be named (something like) un-one-many. Tradition names it many-one.

Doubly confusing since many-one and one-many are not negations of each other!

[My solution: I name $P$ as functional and say in passing that math-books use many-one]

Partial Order

In English partial invariably implies less-than-total.

So if you say to me You are partially correct. it contains the implication: You are correct in abc and wrong in xyz

However in lattice theory etc partial orders can be total! So mathematicians can blithely talk of total partial orders, which to an English-literate, math lay-person would (or should) sound like nonsense!

Partial orders brings me to...

Subset vs Implies

_{Less related to question of inapt adjectives though generally related to inconsistent notation}

Subset and implies have an obvious relation in that: $A \subseteq B ~~~\Longleftrightarrow~~~ x \in A \Rightarrow x \in B$

Yet we hardly notice that the subset has a line below for equal whereas the implies does not.

I certainly had not noticed the inconsistency until someone asked a question here a couple of months ago. Sorry, cant seem to locate it.

The essence of it as I remember: Why is not $\subset$ the symbol for subset — proper or improper — with $\subsetneq$ reserved for strict subset?

People answered with drawing a parallel of $\subset$ with $<$.

IMHO $\subset$ is more related to $\Rightarrow$ than to $<$ insofar as by trichotomy for numbers $x,y$ if $x<y$ is false one of $x=y$ or $x>y$ must obtain whereas two random sets or propositions are more likely to be unrelated to each other.

edited Mar 08 '22 at 14:19

answered Mar 08 '22 at 09:53

Rusi

217
1
7

1

(1) I don't see how this actually answers the question, which is about "perfect squares" (on a website about education, not mathematical language), and (2) some authors use $\subsetneq$ for a proper subset, and $\subset$ for arbitrary subsets. Personally, I think that the least ambiguous notation is $\subsetneq$ for proper subsets and $\subseteq$ for arbitrary subsets, but if it bothers you that much, you would not be alone if you used $\subset$. – Xander Henderson Mar 08 '22 at 12:52
@XanderHenderson I read the question as one of inapt adjectives. [And how they (may) hinder learning] I've made that more explicit in the intro – Rusi Mar 08 '22 at 13:54
@ryang Precisely! So while subset and implies are related as I describe. yet, $P \Rightarrow P$ is trivially true but $A \subset A$ always false. IOW we are not talking of math-facts so much as misfitting terminology. Anyways... Ive expanded that example. Pls check – Rusi Mar 08 '22 at 14:07
Again, many authors use $\subset$ for any subset, and $\subsetneq$ for a strict or proper subset. While I think that your objection to $\subseteq$ is silly, your preferred notation is common enough that you can use it with little fear of causing confusion. – Xander Henderson Mar 08 '22 at 14:14
@Rusi Oh, you meant bad notation rather than bad terminology. Got it. But of course this is a separate issue from this thread; although, come to think of it, the common paedagogical theme may be learning how to be unambiguous in a sea of ambiguity. – ryang Mar 08 '22 at 14:15
1

Tnx @ryang. Changed "bad terminology" to "inconsistent notation". – Rusi Mar 08 '22 at 14:21
1

@Xander Henderson: Related to the ambiguity with the subset symbol $\subset$ is one that often arises in my current line of work, namely the word "contains", which is used both for set membership and for set inclusion. It's one of those things that writers tend to be blind to, thinking of course set membership [set inclusion] is intended -- isn't that what the word means in math? I recently had to rewrite a problem involving basic set operation notions for a certain high-stakes math test because, until I looked at the solution, even I didn't know which version of "contains" was being used. – Dave L Renfro Mar 08 '22 at 15:37
@DaveLRenfro Well mixing up $\subset$ and $\in$ is way more serious than my examples! But I guess its a specific in your context?? And not a generic problem with standard notation/terminology/definitions of the sort I am describing... – Rusi Mar 08 '22 at 15:43
Thank you for this post. I am working as hard as I can, with the small bit of influence that I have, to work on bringing these linguistic and symbolic inconsistencies to light. I will not, for example, use $\subset$ as it is ambiguous, just $\subseteq$ and $\subsetneq$, clumsy though the notations are, purely because of this general ambiguity. And teaching stupidity, because "that's the way we've always done it" does not fit well in my mindset of how the world ought to be. – Prime Mover Mar 08 '22 at 18:51
@PrimeMover You must be young When I was nearly a 3rd my age I thought and felt and wrote and canvassed similarly. Older now I pick dragons more my size. (if you like I can fish out my more impassioned writings on this subject from near 30 years ago) But seriously Chinese are better at math because their language more naturally matches numbers https://amp.goldthread2.com/culture/why-are-chinese-students-good-math/article/3096966. Will you change number names in English? Likewise phonetic languages like Hindi are faster to pick than English https://en.m.wikipedia.org/wiki/Ough_(orthography). – Rusi Mar 08 '22 at 19:08
2

Since we're all SI decimal now how about 100 degrees to a right angle? 10 days to a week; 10 months to the year?? I'm being less sarcastic than I may sound. Just cautioning that you measure your might/passion against the inertial momentum of millennial habits. And chase changes that are effectuable. Consider tau replacing pi – Rusi Mar 08 '22 at 19:11
@Rusi Pertwee's "Doctor Who" was at times indecisive and dithery under extremes of stress. Tough Troughton thought through thorough trough, though. – Prime Mover Mar 08 '22 at 19:45

Use of language: "perfect square". is this useful or a hindrance?

5 Answers5

Many-One/One-Many Relation

Partial Order

Subset vs Implies