6

I am tutoring a student who doesn't really understand how multiplication works or what distributivity is, I want to explain him how distributivity of multiplication over addition on an abstract level works like:

$$ (a+b)(c+d) = a(c+d) + b(c+d) = ac+ad+bc+bd$$

The student seems to struggle in understanding on an intuitive level why the expanding of brackets work in multiplication. Would there be a way to explain the above sequence of manipulation without using any reference to area formulas?

Please keep it as simple as possible.

tryst with freedom
  • 597
  • 5
  • 18
  • 27
    Why don't you want to use area? – Steven Gubkin Dec 06 '21 at 16:07
  • 1
    This student is an adult learner, I feel like area is introducing a new concept to like explain something else. I'd like it to be self contained as possible and as short and simple, so I can move on to the next thing. – tryst with freedom Dec 06 '21 at 16:53
  • 16
    I think you are making a mistake in your approach. While there is certainly a logical path to demonstrating the correctness of this (you have shown it here: applying the distributive property twice), real learning doesn't happen this way. It is far messier. – Steven Gubkin Dec 06 '21 at 17:13
  • 1
    If interested, my non-area method (tailored appropriately to the audience) is discussed in this answer, which I notice for some reason wasn't well received here. – Dave L Renfro Dec 06 '21 at 19:02
  • 1
    Your "non-area" approach seems like the standard area approach with extra steps and limited to natural numbers. – Jasper Dec 06 '21 at 21:53
  • 7
    If the student doesn't really understand multiplication, address that first. – Stig Hemmer Dec 07 '21 at 10:34
  • @DaveLRenfro This is pretty close to how a proof of the distributive property from the Peano Axioms would go (it is cleaner to induct on the $c$ from $a(b+c)$ than the $a$ though). – Steven Gubkin Dec 07 '21 at 12:36
  • Do you want a method that would demonstrate the distributive property for any numbers including fractions and decimals? – Amy B Dec 07 '21 at 15:59
  • 2
    Please use area to explain this. When I first got the distributive property explained using area it clicked immediately. If you teach it axiomatically this property will forever be a vague statement in your students head. If instead you explain it using area it will be grounded on solid intuition because area is something we are all familiar with. – AccidentalTaylorExpansion Dec 07 '21 at 16:41
  • Also the distributive property is one of the fundamentals and it wouldn't hurt to spend some time on it if the student is struggling. – AccidentalTaylorExpansion Dec 07 '21 at 16:45
  • There are two common conceptions of multiplication. First, as you've mentioned multiplication as Area from dimensions, which works well with Real numbers. The earlier (and arguably simpler) that works only with integers is multiplication as something done a repeated number of times. – RBarryYoung Dec 09 '21 at 12:28

10 Answers10

17

This is based on a framing device I used in a Khan Academy comment helping students get an intuitive appreciation of the distributive rule. It is just a description of $a(b+c)=ab+ac$, but it might be enough to jump start a student's intuition.

Every day at work, I eat a lunch of two sandwiches and three cookies. I like to be organized by packing five lunch boxes on the weekend for the upcoming work week. That way, I can just grab a lunch box out of my refrigerator each day on the way to work. At the beginning of the work week, how many sandwiches and cookies do I have prepared?

Students with a solid understanding of multiplication word problems don't seem to have trouble correctly calculating that there are ten sandwiches and fifteen cookies. When prompted, they get that they can treat counting the sandwiches and counting the cookies as two separate problems.

All that remains is showing how algebra just gives us a slightly different notation that allows us to describe the situation in a single expression. In this example, $2S+3C$ is an expression that models the contents of a lunch box (which can't be simplified because sandwiches and cookies are not "like terms") and 5(2S+3C) is an expression that describes the contents of five lunch boxes. Once you understand that, the distributive rule just verifies the students' own calculation that $$5(2S+3C)=(5\cdot2S)+(5\cdot3C)=10S+15C$$

Keep in mind that I came up with this inquiry for an online community. If I had the opportunity to sit at a table with an individual student, using manipulatives would be much more powerful. For instance, draw four circles on a piece of paper and put three pennies and two paper clips on each circle. Then sweep all the pennies and paper clips into a single pile and ask how many of each there are. Again, the key is helping students understand that they already knew the answer. The thing that makes the distributive property cool is not that it is a new fact, but rather that algebraic notation lets us talk about subconsciously familiar numeric relationships that were previously much harder to express.

Matthew Daly
  • 5,619
  • 1
  • 12
  • 45
  • 3
    What do S and C represent here? It is not the number of sandwiches and cookies. This seems to explain the distributive property of something like a module, and not really the distributive property of pure numbers. – Improve Dec 07 '21 at 06:40
  • This can be made more direct (without the abstract "terms") by using an additive numerical property of the foods, like weight or calorie content. Say each sandwich and each cookie is 200 calories. I start with a pile of sandwiches totaling 2000 calories and a pile of cookies totaling 3000 calories. I pack 5 lunches each containing 1000 calories. – nanoman Dec 07 '21 at 07:39
  • Real life application here! – nanoman Dec 07 '21 at 07:43
  • 4
    @Improve I don't want to enter a discussion of graduate-level mathematics on a question where the OP specifically asked to keep it simple. But manipulating polynomial expressions in multiple unknowns that may or may not have intrinsic numeric values is a part of pre-algebra education. Also, since any ring $R$ is a trivial example of a left $R$-module, this example does justify the distributive property of "pure numbers" in addition to more esoteric mathematical structures. – Matthew Daly Dec 07 '21 at 09:16
  • I misunderstood and thought you were showing that 5(2+3) = 52 + 5*3. – Improve Dec 07 '21 at 22:17
17

It depends on how the student conceptualises multiplication. First, find that out. Then design an approach that uses it.

For example, if they think of multiplication as repeated addition, then you might try examples like:

$3\times(4+5)=(4+5)+(4+5)+(4+5)=(4+4+4)+(5+5+5)=(3\times 4)+(3\times 5)$

This approach gets messy trying to multiply out more than one bracket, so has to be taken slowly. Always do the brackets one at a time with this approach.

If they think of it as counting objects arranged in a rectangle, set out some objects on the table, or draw some pictures. How many red diamonds are there here? How does this picture represent the statement: $3\times(4+5)=3\times 4+3\times 5$?

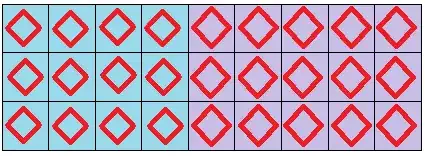
Rectangle of squares

Counting objects arranged in a rectangle is visually intuitive, which helps a lot, and makes an easy starting point to move on to interpreting it as an area. I personally think it's an easier approach than rearranging symbols as above. But the important thing is to find out where they are now, and then chart a course from there to where you want to go.

Also, start with concrete examples. Then illustrate the concept with pictures and diagrams. Finally, present the abstract/symbolic, once the basic intuition is there for it to connect to. "Multiplying out brackets" is the symbolic/abstract end stage. If they have been only shown the symbolic manipulation, that would explain why they have no intuitive grasp of why following the procedure works, and you won't get far without going back and introducing the supporting concepts.

If they haven't come across the area analogy, then I agree it is going to make it more difficult to introduce it right in the middle of explaining multiplying out brackets. But this ought to be telling you that you're trying to do things too fast, and out of order. Don't even think about teaching 'multiplying out brackets' until you have first taught 'multiplying', with an intuitive, visual analogy like areas or counting in rectangles or fixed-size boxes. (Like 'Widgets come in boxes of three. If we have four boxes and add five more boxes, how many widgets?') Then when you teach each abstract method, you have a visual/intuitive picture to link it back to.

If you want to use several such analogies/pictures, then introduce them all up front when teaching what multiplication is. Then later, when you run into difficulties with one approach, you have alternatives to fall back on, and you don't have to be introducing new topics in the middle of an explanation.

Nullius in Verba
  • 186
  • 2
  • 12
    The fun thing here is that the student may not have a conceptualization of multiplication. For example this seems like a likely line of questioning: "What is 2 times 3?" "6." "How do you know?" "I just know." "What if someone told you it was actually 5?" "We would look it up, and it would be 6..??" but this conversation is still productive and will eventually lead to this answer being correct. – Chris Cunningham Dec 07 '21 at 14:34
  • 1
    @ChrisCunningham: Personally, I blame the multiplication tables for this. Yes, they're helpful to memorize, no, we shouldn't consider that to be "learning multiplication." Far too many elementary school classes dedicate a tiny amount of classroom time to "multiplication is repeated addition," and then they drill the heck out of "did you memorize all the numbers correctly?" – Kevin Dec 08 '21 at 19:15
  • @Kevin The CCSS attempt to counter this by promoting a strong emphasis on conceptualization; the approach you describe hasn't been the national practice for at least a decade. Now, there are other problems (e.g. overreliance on teaching alternate algorithms as a substitute for understanding) but the pendulum can now be considered to have "swung the other direction." – Opal E Dec 08 '21 at 19:30
  • @Kevin I find the opposite - my kids understand multiplication but have to use their fingers way to much for single digit multiplication facts! – corsiKa Dec 09 '21 at 00:06
  • 1
    Obligatory curmudgeonly link: https://www.maa.org/external_archive/devlin/devlin_06_08.html . – Xander Henderson Dec 09 '21 at 01:30
  • @XanderHenderson: I read the article, but still don't understand what the argument is, or why it's wrong to explain multiplication as repeated additions. Once you can multiply integers, you can explain fractions, and then you can multiply fractions with repeated additions. – Eric Duminil Dec 09 '21 at 11:59
  • 1
    @EricDuminil Express $\sqrt{2} \pi$ using repeated multiplication. – Xander Henderson Dec 09 '21 at 13:14
  • @XanderHenderson: You can come arbitrarily close to the result with fractions, so you could calculate $\frac{99}{70}\frac{355}{113} = \frac{99355}{70*113} \approx 4.443$. You'd need infinite steps to get the exact decimal representation, just like you would with any other method, BTW. "Repeated addition" isn't wrong IMHO, it's just that it doesn't apply to every domain, and needs to be refined, which is common in mathematics. The article you've linked would simply be much better with a lighter tone, and fewer absolute statements. – Eric Duminil Dec 09 '21 at 13:39
  • So multiplication in the real numbers is (really) the limit of a sequence of approximations, where each approximation is really the repeated addition of rational numbers (I'm still not sure that $\frac{2}{3} \cdot \frac{17}{11}$ is as repeated addition, but I'll let that go, for now)? So, in order to understand what multiplication in the real numbers is, you first have to tell children that multiplication is repeated addition, then say, "Well, actually, in the real numbers, multiplication is something completely different, and we need limits to define it." – Xander Henderson Dec 09 '21 at 13:42
  • 1
    So you are initially presenting multiplication as one thing, then changing the rules and defining it as something else. This is exactly what Devlin is arguing against. – Xander Henderson Dec 09 '21 at 13:44
  • And, if you are interested, Devlin has written more on the topic: https://www.maa.org/external_archive/devlin/devlin_0708_08.html and https://www.maa.org/external_archive/devlin/devlin_01_11.html . There is another post in the series, but I can't seem to find a link at the moment. There are also (obviously) many dissenting opinions out there. However, I am engaged in a polemic, and I don't think that it is my responsibility to do the other side's work for them. :) – Xander Henderson Dec 09 '21 at 13:56
  • 1
    @XanderHenderson: Refining is not the same as changing the rules or the definitions. It would be like saying that it's wrong to define cosine and sine with the lengths of a right triangle, because you have to change the rules and use Euler's formula instead once you want to use a complex number as an input. I don't see any problem in needing limits for multiplication of real numbers, since you need limits anyway to define the real numbers (https://en.wikipedia.org/wiki/Least-upper-bound_property). Feel free to show me how you'd calculate $\sqrt 2 *\pi$. – Eric Duminil Dec 09 '21 at 14:03
  • 1
    You cannot represent real multiplication as repeated addition. You can only represent it as the limit of a sequence of repeated additions, which is an entirely different kind of object. And the problem is worse in other spaces. If $A,B \in M_{n\times n}(\mathbb{C})$, what is $AB$ as repeated addition? In this context "multiplication is scaling" makes quite a bit of sense ($A$ and $B$ denote linear maps, and there is a reasonable way of describing how one linear maps scale each other). Repeated addition? Not so much. – Xander Henderson Dec 09 '21 at 14:09
  • @XanderHenderson: For $\frac{2}{3}*\frac{17}{11}$, you'd multiply 2 and 17, then 3 and 11 separately. I'll handwave the division, just like Devlin did in his article. And thanks but no thanks, I'm not interested in more articles from the same guy with the same opinion. Let's agree to disagree! – Eric Duminil Dec 09 '21 at 14:10
  • 1
    @XanderHenderson It's called "lies to children" and it's an important and honorable profession. Probably someone taught you that 1) the Earth is round (no: it is an oblate spheroid), 2) the Earth goes around the Sun (nope: the Earth and Sun both go around their barycenter--but then also nope to that, because really their motions constantly being perturbed by all of the other stuff in the universe), 3) 1+1 = 2 (nope: not in binary). Do you feel like any of those things you were taught have hindered your further understanding? https://en.wikipedia.org/wiki/Lie-to-children – user3067860 Dec 09 '21 at 14:20
  • 1
    @user3067860 I am familiar with the concept of lies-to-children. However, there is a difference between presenting a simplified model (yes, the Earth is a 3-ball, to a first order approximation (and I would argue that an oblate spheroid is round, so saying that the Earth is round isn't even a lie); yes, the Earth does go around the sun, more or less). Good lies-to-children are stories which can be refined, but which don't require fundamentally rewriting or reteaching definitions. Again, I still don't know what $\frac{2}{3}\cdot \frac{17}{11}$ means as repeated addition. – Xander Henderson Dec 09 '21 at 14:30
  • 1
    I can compute $\frac{2}{3}\times \frac{17}{11}$ by multiplying across the top and bottom, but that doesn't tell me what it means to add $17/11$ to itself $2/3$ times (or vice versa). Telling students that multiplication is repeated addition (and not just that repeated addition is a useful way of computing multiplication in the natural numbers) eventually requires a complete tear-down and reconstruction. – Xander Henderson Dec 09 '21 at 14:31
  • 1
    In any event, this comment thread has gone way off-topic, so I am going to bow out. – Xander Henderson Dec 09 '21 at 14:32
  • 1
    Repeated addition seems a type of multiplication to me, but not the other way around. However, non-symmetric claims are hard to teach. – Discrete lizard Dec 09 '21 at 17:05
4

If you want to avoid area, then the next closest thing is arrays.

See:

https://www.khanacademy.org/math/7th-grade-foundations-engageny/7th-m2-engage-ny-foundations/7th-m2-tc-foundations/a/distributive-intro

https://makemathmoments.com/progression-of-multiplication/

If arrays are still too close to area, then you'll have to think of another "good" way to visualize multiplication in general. If it truly is a good way, then the distributive property should come naturally within it.

Aeryk
  • 8,013
  • 18
  • 44
  • 3
    Agreed. I wouldn't even view this as "avoiding" area because when I think of modeling multiplication to figure out its properties, arrays are THE fundamental objects. Area comes next by viewing a rectangle as an array of squares. – Thierry Dec 07 '21 at 02:53
4

Reteach multiplication of multi-digit numbers (eg $12 \times 34$) by pen and paper in terms of $(10+2)(30+4)$. You should reconcile their early memories of arithmetics with this somewhat new concept of distribution.

Then redo the same problem but break the factors into different numbers, eg $(10+2)(30+4) = (5+7)(28+6)$ to allow them to see it has nothing to do with the number 10 or decimal representations.

okzoomer
  • 341
  • 1
  • 11
1

Despite your requirement, I recommend using array and area models.

I suggest engaging them in tasks such as the following:

Write as many algebraic expressions as you can (using integers and the 4 operations) to count the number of x's in the following diagram:

xxx
xxxxx
xxxxx
   xx
   xx
   xx
xxxxx

Possible answers include $3\cdot 4+2 \cdot 6$ or $7\cdot 5 - 2 - 3 \cdot 3$.

Also engage them in the other direction:

Can you draw a picture of x's which has $5\cdot (2 + 4) - 3\cdot 3$ dots in it?

Work your way up to expressions like the one you are struggling with. Be sure to pair the geometric work with symbolic translations as much as possible.

Steven Gubkin
  • 25,127
  • 4
  • 61
  • 110
1

My highschool teacher would say

If you have two times three apples and five plums, you have six apples and ten plums. That is, $$ 2(3a+5p)=2\times3\,a+2\times5\,p $$

Martin Argerami
  • 1,078
  • 5
  • 11
1

I recommend Cuisenair Rods. While one could argue that their use essentially breaks down to area it's very intuitive and accessible. As always, a physical involvement like manually handling the rods aids "grasping" an issue.

If you arrange, say, 6 rows of 5+2 rods you can split them in a pile of 2-rods and a pile of 5-rods before adding the rows, or leave them connected and count the entire rows (whose length is 5+2 each); there is no easier explanation than that.

Peter - Reinstate Monica
  • 715
  • 3
  • 9
  • While great for the fundamental "6(5+2) is this many, how else can we group them?" concept, physical rods seem more of a classroom thing. They also don't seem as good with unknowns a,b,c,d (sure, you can imagine c rods of length a and b, but without known lengths you may as well simply write: a,b;a,b;a,b;a,b). – Owen Reynolds Dec 08 '21 at 15:38
1

If you do not want to use area, here is another way:

You have 9 bracelets. Each bracelet has 7 beads on it. Now you put 4 bracelets on your left hand and 5 on your right.

How many beads you have in total?
How many beads you have on your left hand? How many on your right?

Points of discussion:

  1. With any number of bracelets, you can count beads by removing them from the bracelets one by one. On or off the bracelets, you have the same number of beads.
  2. To get the total in both hands, you can count the beads on the left and the right and then add, or, take all bracelets down and count. Either way the number of the beads is the same.
  3. If you have some number of a thing in one hand and some number in another, then you have the sum of counts of the thing in both hands.

The likely reaction to this, once they get it, is "meh, of course" because it is so trivial, that it does not even seem to be something of use.

So the main task is to connect the idea to the symbolic identity a(b+c)=ab+ac, so that they understand that it serves as a model for the reasoning above.

When both factors are sums, of course demonstrating with areas is much simpler and usually more satisfying. But if they understand the above you can also convince them, that the result is the same if the distributive property is applied twice.

BKE
  • 1,282
  • 8
  • 16
0

2 apples + 3 apples = 5 apples

Why?

2 apples + 3 apples = (2+3) apples = 5 apples

The "=" on the left is distributivity.

Alexander Kurz
  • 1
0

Assuming you get them through the first part, about how a(b+c) distributes, the second part is just distribution again. It's just symbol manipulation. Think of (a+b), for now, as a single value. Then (a+b)(c+d) gives (a+b)c + (a+b)d by simple distribution.

I feel like many students learn FOIL so they can go straight from (a+b)(c+d) to the full ac+ad+bc+bd expansion. But FOIL is just a derived shortcut. You're showing the actual process, where (a+b)(b+c) is distribution twice.

I think NulliusInVerba really has it for the first part. Arrays are merely a visual way to show "multiplication is a shortcut for repeated addition". When we sketch 3x6 as a 3 by 6 rectangle, that's just a pretty way to say "3x6 means 6+6+6, which we can think of as 3 strips of 6's, side-by-side".

With "repeated addition", x(y+z) is defined as (y+z)+(y+z) ... x times. Commutativity and association then let us regroup them as x y's and x z's. Reversing the rule (multiple additions can be rewritten as multiplication" gives us the distributed xy+xz.

Owen Reynolds
  • 231
  • 1
  • 4