The imagined students are in elementary school, say around 9-13 years old.
I want to use rather precise terminology when talking to my students. However, it seems like we typically use the same terminology for a geometric figure and for its boundary.
Does the word "triangle" refer to the $2$-dimensional geometric figure or the $1$-dimensional geometric figure? It seems to me like we kind of treat "triangle" to mean either, or even both at the same time.
There are similar issues with other terms, like "square", "circle" and "cylinder". Here I can imagine the word "cylinder" also being used for cylinders open at the bottom, or a cylinder open in both ends. There seems to be some distinction when talking about "balls" and "spheres".
I fear that when the terminology is not precise enough that this will lead to unexpected problems when defining and working with other concepts later on. For instance, if one defines a triangle as some union of edges and vertices, then one needs to be a bit careful when defining the area of the triangle.
Many of the geometric figures are so elementary that they are deeply rooted in daily language, and there seems to be no great solution.
I have played with the idea of calling things something like "1D-triangle" and "2D-triangle", but this seems to make things worse and I have not come up with good alternative terminology.
My current go-to would be to tell my students something like "We call this a triangle, but we also call this a triangle. Sometimes the distinction matters, but most often it is clear from context." Another possibility would be to just let the students realize the ambiguity themselves. I don't really have any evidence that suggests that this actually is an issue.
Question
What can (and should) an educator do about ambiguous terms like "triangle", "square", etc?
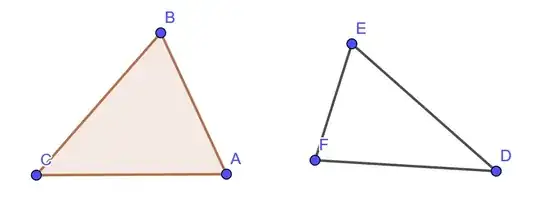

Improvemeant "closed polygonal chain with 3 vertices". "1D Square" would be a "closed polygonal chain with 4 vertices, where all segments have equal length" – user28434 Jun 02 '21 at 17:16