Which product of single digits do children usually get wrong?

Question

^{(I was inspired by the comments in this answer to ask this question.)}

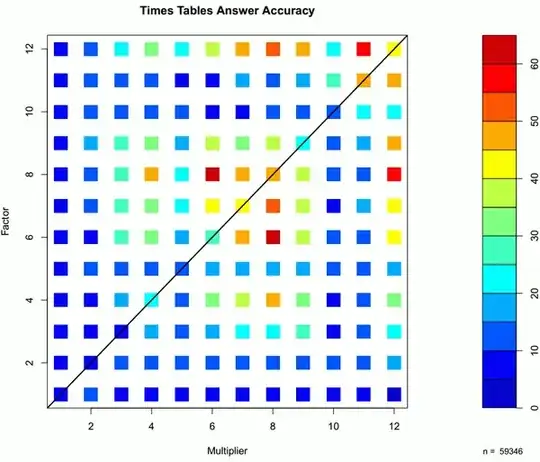
I have some multiplication table cards from Kumon that have a list of commonly mistaken multiplications: $7\times 8, 4\times 8, 11\times 12, 7\times 9, 6\times 7, 12\times 8, 4\times 7, 6\times 8, 9\times 12, 8\times 9, 11\times 11$, and $6\times 9$ (in this order).

I assume that this is based on data they obtained from the numerous children who have answered their worksheets.

Is there some other source (a study, perhaps) that lists the products of single digits that children usually get wrong?

Anecdotally, 7x8 was the only I struggled with when I was first learning my tables. Right before it was taught to us, my teacher said out loud "and 7x8 is the only one I struggle with sometimes....sometimes I say it's 54 but it's really 56."
To this day I have to stop and take a moment to think "is it 54 or 56???" — ruferd, Mar 03 '21 at 14:51
It was $6\times 7$ for me, I always resorted to $6\times 6 + 6$ or similar tricks. — Adam, Mar 03 '21 at 15:44
For $7 \times 8$, try doubling $7 \times 4$ as a way of remembering it. Or thanks to @Adam try $8 \times 8 - 8$. — J W, Mar 03 '21 at 16:14
4th grade teacher had us, when we felt ready, take a quiz on these multiplication tables; when you did it, you could have free time instead of continuing to study. I was good with numbers, and the first to try it. I got one wrong, mixing up 7 × 8 and 9 × 6. I had to wait a day to try again, and I've never mixed them up since! — Scott Sauyet, Mar 04 '21 at 04:17
@ruferd: 7x8 is easy to recast as 8x8 - 8, and power-of-2 stuff is hard-wired into the brains of many computer geeks so that makes it very easy for me. (Especially since multiples of 8 come up often when dealing with bit shift counts for whole numbers of bytes, and other low level SIMD / bithack stuff that I spend a lot of time on. So I fully realize that I'm not a typical person learning their times tables :P I tend to have to think harder about multiples of 7 than most others, probably because it's the largest single-digit prime so resists many simple tricks.) — Peter Cordes, Mar 04 '21 at 10:36
Not exactly what you asked, but the TT Rock Stars online game maintains an individual heatmap of which products the player gets right and wrong. I presume they use this to schedule difficult questions more frequently. — paj28, Mar 04 '21 at 11:03
Funny how the confusion about 7 × 8 and 9 × 6 (which one is 54 and which one is 56) is so common, that has always been a challenge for me as well, it's probably the only pair I need to really think about rather than just "know". — jcaron, Mar 04 '21 at 11:15
@ruferd Just remember it like this: $56 = 7 \times 8$ (i.e. 5,6,7,8) — Jann Poppinga, Mar 04 '21 at 13:14
And if comparing $7 \times 8$ and $9 \times 6$, just remember that (for a fixed sum) the product will become larger if the numbers are closer together. That's often more useful to remember than a specific product, anyway. — Misha Lavrov, Mar 04 '21 at 20:15
Is there any plausible psychological hypothesis that explains the data on difficulty? — Joseph O'Rourke, Mar 05 '21 at 22:29
I want to add that the answers depend on the language and not on the math itself. The only factor is how rhyme-y it is to read out loud each equation. — MCCCS, Mar 06 '21 at 19:26
@JosephO'Rourke, there most likely is, but I'm not familiar with it. — JRN, Mar 07 '21 at 01:18
Clearly, Adam and J W are reporting real experiences which I, for one, see as too common.
… for 6×7, I resorted to 6×6+6… why?

… for 7×8, try doubling 7×4… again, why use tricks?

I see how thin a limb I sit on yet why promote theory over simple evidence?

Adam, J W et al clearly show they saw learning times tables not as a rote task but as something to be understood, at which they failed. Of course they did!

Which teacher here doesn't see that children getting any product of single digits wrong is nothing to do with children or numbers and that that leaves… sorry: teaching! — Robbie Goodwin, Apr 29 '23 at 18:34

Adam · Accepted Answer · 2021-03-04T23:41:39.453

46

https://www.theguardian.com/news/datablog/2013/may/31/times-tables-hardest-easiest-children

There are links to a dataset in the article. As far as I can tell, this isn't a formal study:

But some new data generated by pupils at Caddington Village School in Bedford sheds light on which multiplications are actually the hardest – and how kids do overall.

The data is generated by an app produced by an app developed by education tech firm Flurrish, and in total the 232 children who participated produced more than 60,000 answers. Here's how they did

So the data is of unknown quality, but the graph is both pretty and pretty believable. (Except that I'd probably label the graph below inaccuracy rather than accuracy.)

It's notable that the data is slightly asymmetric but I'm unsure if that is statistically significant. i.e. Do kids use commutativity?

edited Mar 04 '21 at 23:41

answered Mar 03 '21 at 15:42

Adam

5,528
18
35

2

The row of 12 and the column of 12 is interesting! – ruferd Mar 03 '21 at 18:24
9

Also the row/column of 10 that drops accuracy for 1011 and 1012. They've memorized a rule, but seem slightly uncertain if the rule applies to numbers higher than 10. – ruferd Mar 03 '21 at 18:26
@ruferd Of course English has the same uncertainty. You have words of the form sixty (six+ty) etc, but then it jumps to "one hundred and ten" instead of "eleventy" and "twelvety". Maybe related, maybe not. – Adam Mar 03 '21 at 18:55
Good, good, good, gooood Eleven/Never gave me any trouble til after nine... – Exal Mar 04 '21 at 10:32
It's interesting how the results don't match at all all the comments on the question. The big issue seems to be with 6 × 8 here, while many commenters had issues with 7 × 8 and/or 9 × 6. – jcaron Mar 04 '21 at 11:21
12

Is it common to teach multiplication tables up to 12 in english-speaking countries? Or is this maybe specific to the UK (due to the historical 12 pence in a shilling) and the US (due to the still current 12 inches to a foot)? In the French system we only learn them up to 10. Or at least we used to, though I doubt this has changed. – jcaron Mar 04 '21 at 11:24
2
The image has gone from the Guardian article, but the data is still available. According to the article n=232 (i.e. 232 children), so since (in 2021) the school has an age range 3-11 and an enrolment of 360, this looks like year 1 and up. Given this the results overall aren't that bad. But there are some salient features in the data:
- Some items are answered with much lower frequency than others. Least answered is 11 x 12 with 208 answers, most answered 5 x 7=6 with 547 answers.
- Speed varies 1x1 averages 2.3 s, 12 x 9 7.94 s.
- 1 x1 was answered wrongly almost 10% of the time.
– Rich Farmbrough Mar 04 '21 at 12:00
1

@jcaron For me (US, Pennsylvania) at that age, our times tables were up to twelve, but the focus seemed to be mostly on 0 though 10. – Adam Mar 04 '21 at 12:59
4

What surprises me about this chart is the asymmetry. 7 × 6 is wrong considerably more often than 6 × 7. Likewise for 12 × 11 vs. 11 × 12, 12 × 7 vs 7 × 12, etc. Not sure if this is just noise in the data or kids confused about commutativity? – Darrel Hoffman Mar 04 '21 at 14:00
1

@DarrelHoffman I want to make a joke about people not becoming commuters until they get adult jobs. – Barmar Mar 04 '21 at 17:03
13

@DarrelHoffman: Looks mostly like noise to me. I played with the raw data a bit, and none of the results seem to be more than 2 standard deviations away from what would be expected under the null hypothesis of commutativity. Furthermore, the biggest deviations are for "easy" pairs like 6×3 vs. 3×6 (74% vs. 82% correct, 1.96 σ), 12×1 vs. 1×12 (90% vs. 95% correct, 1.66 σ) and 10×3 vs. 3×10 (88% vs. 92% correct, 1.56 σ). For 7×6 vs. 6×7 the deviation is less than 0.6 σ, easily explained by chance. – Ilmari Karonen Mar 04 '21 at 17:55
1

@jcaron I think (entirely without evidence) that it's because of "dozen" (which Wikipedia tells me is derived from a French word). In English we use "dozens" for numbers between about 12 and 100 or so, and commonly foodstuffs or other items are packaged in groups of 12 (a dozen eggs). So you might need to know that if you need, say, 36 eggs then you need 3 dozen eggs. https://english.stackexchange.com/questions/44975/why-do-we-not-say-tens-of – user3067860 Mar 04 '21 at 18:51
3

The asymmetry is significant and expected. If you had presented a symmetric plot I would have downvoted because I know it's asymmetric. – Joshua Mar 04 '21 at 19:11
@jcaron I hadn't noticed before your Comment, but that really is another example of how it's not true that the decimal is better or easier to use, even though it happens to be easier to teach! – Robbie Goodwin Mar 04 '21 at 20:25
1

@jcaron - I am in the US and recall that in the 60s/70s the table was 12x12. And it was common to memorize it by 5th grade or so, age 10-11. Today, I see too many high school students who were raised on calculators, and will not have even the lowest quarter memorized. – JTP - Apologise to Monica Mar 04 '21 at 23:09
@user3067860: French has words for not only "douzaine" [group of twelve] but also "dizaine" [group of ten]. Not sure which is used more commonly. – supercat Mar 05 '21 at 20:52
1

@Joshua Care to elaborate? – preferred_anon Mar 06 '21 at 10:40
6x8 surprised me, too. Six times an even number should be easy because of 6=5+1, but I suppose many children do not learn multiplication this way. – Carsten S Mar 06 '21 at 12:44
2

" both pretty and pretty believable." --> Yes it is pretty, but table labeled as accuracy with values in colors 0- 65%. Table should be labeled inaccuracy or valued 100 - 35%. – chux - Reinstate Monica Mar 06 '21 at 14:36
" both pretty and pretty believable." --> True, except the table is based on correct/(correct + incorrect), not correct/(correct + incorrect + (some_factor*unanswered)). The unanswered are not randomly occurring. Any analysis needs to consider that unanswered are more likely reflecting incorrect than correct had the test taker filled it in. – chux - Reinstate Monica Mar 06 '21 at 14:52
UV for an good an attractive answer, but perhaps add a direct answer to the question "Which product of single digits do children usually get wrong?", perhaps along the lines of "8 * (4, 6, 7 or 8) in either order are the certainly the troublesome products". – chux - Reinstate Monica Mar 06 '21 at 14:58
@chux-ReinstateMonica Barring your third comment, which I feel is evident from the table, I agree and in the first case agreed in the text. However, this was not my study and I did not personally produce the figure. If you would like to produce an improved figure, I would happily approve the change. – Adam Mar 06 '21 at 15:40
@preferred_anon: Most elementry school kids don't compress the table by rearranging the inputs naturally. This takes some time to catch on. My memory sais the asymmetry should be between 87 and 78 and if I'm interpreting "multiplier" and "factor" right, 87 has more errors than 78 which again is as I expect. The table shows the same problem at 98 and 89 in the same direction, which I did not expect only because we were taught to do nines by subtraction. – Joshua Mar 06 '21 at 17:31
1

@Joshua: The asymmetry indeed exists, but it's not statistically significant at the sample sizes used in the study. (Whether or not a significant effect would show up in a larger study is a different matter.) The discontinuous color scale in the chart also overemphasizes some even rather small asymmetries: for example, the success rates for 6×7 and 7×6 are 52.8% and 55.4% respectively, where the 2.6% difference is completely indistinguishable from random noise. But they look very different on the chart, because the color change at 55% success (= 45% failure) is very noticeable. – Ilmari Karonen Mar 07 '21 at 00:41
(FWIW, my personal conjecture would be that there's indeed a real asymmetry for basically the reasons you suggest, but that it shows up mostly for very easy tasks — like 1×N vs. N×1 — because those are the ones that only the youngest kids will make mistakes on. By the time they actually learn to answer harder questions like 7×8 correctly with a non-negligible probability, many of them will also have figured out commutativity. But while I can sort of see hints of this in the data if I squint at it hard enough, there's just not enough data to say anything for sure.) – Ilmari Karonen Mar 07 '21 at 00:48
@IlmariKaronen: I'm not extrapolating from this data. I already knew what answer to expect up through 8x8. I suspect commutativity isn't used because of speed drills and commutativity is slower than not, but that conflicts with 9x and x9 by subtraction. – Joshua Mar 07 '21 at 00:58
3

@Joshua: Sure. I'm just saying that, while you could well be right, it's also possible that your personal experience is anomalous. And the actual, non-anecdotal data that we have doesn't really support your claims. It also doesn't disprove them, but it does imply that, if the effect you describe does exist, it's not strong enough to be visible in this study. All the apparent asymmetries in the data are perfectly well (p = 0.228 using a Pearson chi-squared test for independence between correctness and factor order; χ² = 74.229 with 66 degrees of freedom) explained just by random sampling noise. – Ilmari Karonen Mar 07 '21 at 03:03

Which product of single digits do children usually get wrong?

1 Answers1

Linked