Pros and cons of randomised question generation

Question

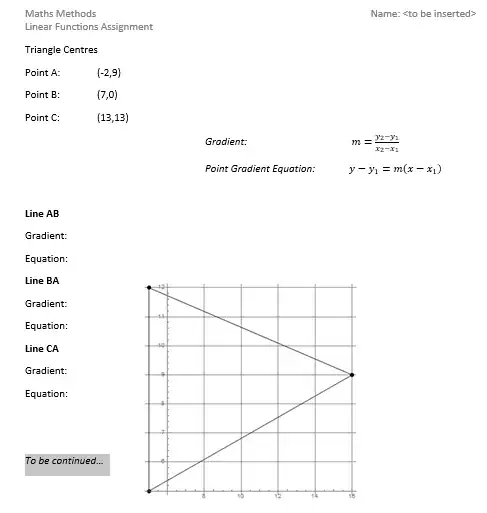
I am developing an assessment piece where the content is the same but the particular numbers are different for each student. It involves finding Triangle Centers given points using coordinate geometry. The particular skills it is assessing (for/as/of) are

• calculating distances, gradients and midpoints
• forming equations of lines
• perpendicular gradients
• simultaneous equations
• graphing points and lines

I am giving each student different randomly generated vertices and asking them to work out 4 triangles centres graph the results. As I've written it is quite guided with the main tasks being calculations between suitably chosen points and graphing. I'll be generating individualised answers as well. See below for a draft.

(I am using Mathematica to generate the initial points and answers including graphs. I export these to Excel and mailmerge them in Word. )

What are the pedagogical issues at play? References welcomed! My own ideas are shown below. I am not so interested in the technical issues involved (Google "latex random test").

Pros

• To encourage students to share skills not answers
• To give students a sense of ownership
• To combat cheating (not a concern in my case, it is more assessment for learning)

Cons

• Difficult to create individualised questions, needs a thorough understanding of the problem and it's algebraic solution
• Unintentional differenation (eg one set of numbers may require a much easier solution than another)

I have particular objective in mind for this project at this stage (paper based, an activity not a test, papers should be of the same difficulty, I like this triangle centres task), but there are some obvious extensions (other maths content, differentiation, automated marking).

Update Having run this in highschool class the main feedback I got was that it was too challenging for most. The most important pedagogical thing which emerged was the need to differentiate. To modify the task to make it easier one could:

• present a partial solution

• algorithmically, select points which have more simple intermediate steps.

Both of which require more work for me! Hence, it is "difficult to create individualised questions, needs a thorough understanding of the problem and its algebraic solution."

Answer 1

Here are some problems I have run into:

1. If problems are randomly generated with unlimited attempts on a computer, then pattern matching is a real problem. Maybe the question is to calculate the radius of convergence of the power series $\sum_1^\infty k(\frac{x-a}{c})^n$ for various $k, a, c$. The students will just guess randomly one of the constants in the expression or its reciprocal until they get the right answer. Then they will memorize which guess is correct, and use it to "solve" many more such problems. This exercise accomplishes nothing. Students will always find the easiest way to play the game, which will often circumvent the concept you thought you were trying to get them to engage with.
2. It is quite difficult to fully debug randomly generated problems. You will often end up with some cases which are unsolvable or which have physically nonsensical solutions (people who weigh less than a mouse, etc).

Answer 2

To encourage students to share skills not answers

This is great in principle, but the question in my mind, based on your sample, is what would be the intellectual content presented by one student to the other. Because the problem is stylized and you're generating a lot of them, the danger might be that your students would infer that the important thing here is to learn to execute an algorithm, without any conceptual understanding. So maybe student A succeeds in getting the right answers to their problem, based on a model you did on the board. Then student A shows their scratch work to student B, who works through the same algorithm with their numbers.

Now you could say this is fine, and they've successfully shared a skill. A has helped B to learn. But it may be that they don't understand the concepts, and therefore their mastery is basically fragile and useless. All they know how to do is fill out a worksheet with exactly this stylized form.

I definitely see this happening with physics students at my school, where some of the teachers use a commercial answer-checking system provided by the book publisher. Many students pay for a monthly membership with a sleazy web site called Chegg, which provides them with worked solutions to all the problems. The numbers are different, but the students just work through the steps with their numbers. They don't understand what they're doing, and their skill doesn't generalize to other problems.

What has worked better for me is to take the time to write problems that are actually qualitatively different, and then randomly assign different problems to different students. Here are two problems I assign that basically use the same skills and are at comparable levels of difficulty, but differ from each other in qualitative ways:

1. Aircraft carriers originated in World War I, and the first landing on a carrier was performed by E.H. Dunning in a Sopwith Pup biplane, landing on HMS Furious. (Dunning was killed the second time he attempted the feat.) In such a landing, the pilot slows down to just above the plane's stall speed, which is the minimum speed at which the plane can fly without stalling. The plane then lands and is caught by cables and decelerated as it travels the length of the flight deck. Comparing a modern US F-14 fighter jet landing on an Enterprise-class carrier to Dunning's original exploit, the stall speed is greater by a factor of 4.8, and to accomodate this, the length of the flight deck is greater by a factor of 1.9. Which deceleration is greater, and by what factor?

2. In college-level women's softball in the U.S., typically a pitcher is expected to be at least 1.75 m tall, but Virginia Tech pitcher Jasmin Harrell is 1.62 m. Although a pitcher actually throws by stepping forward and swinging her arm in a circle, let's make a simplified physical model to estimate how much of a disadvantage Harrell has had to overcome due to her height. We'll pretend that the pitcher gives the ball a constant acceleration in a straight line, and that the length of this line is proportional to the pitcher's height. Compare the acceleration Harrell would have to supply with the acceleration that would suffice for a pitcher of the nominal minimum height, if both were to throw a pitch at the same speed.

This particular pair of problems is actually from a set of 5. So certainly a couple of my students can get together at Starbucks and work on their homework together, but it's unlikely that they were both assigned the same problem. Therefore if they help each other, they are more likely to be giving help at the conceptual level, not the algorithmic level. One student can't just walk through the other student's algorithm.