5

Different people use different mental models, such as Webb's DoK (depth of knowledge), CCSM (Common Core State Standards) aspects of rigor, and Bloom's Taxonomy. At a high level, here's how I'm thinking about how they relate to each other (the mapping is obviously imperfect):

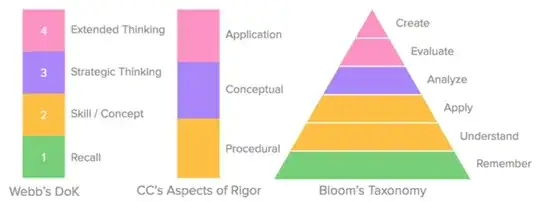
enter image description here

My question is this:

Which mental model is most useful when thinking about math education: Webb's DoK, CCSM's Aspects of Rigor, or Bloom's Taxonomy? Are there others?

Mike Pierce
  • 4,845
  • 1
  • 20
  • 56
Cameron Christensen
  • 349
  • 2
  • 8
  • 8
    Although I'm sympathetic to the understandable need to concretize ("reify"?) these things, my most snarky response is something along the lines of criticizing this idea as an analogue of formalizing how to eat a sandwich at lunch. True, the advice to take a napkin, and not eat anything bigger than your head (from "Farside"), and so on, is obviously good, but (also within mathematics itself) I am (perhaps regretfully) unconvinced that formalization in these contexts is ... accurately relevant. Yes, maybe suggestive. But going off on a tangent, that may be misleading, and time/effort-wasting. – paul garrett Feb 23 '17 at 23:57
  • 1
    My limited acquaintance with CC and Bloom's taxonomy has not encouraged me to have much respect for either. CC seems like a mushy, chaotic political compromise written by a committee to satisfy the desires of politicians. Bloom's taxonomy is used at my school as a fuzzyheaded, formalistic administrative requirement in the curriculum process. This sort of stuff impresses me as the kind of nonsense discussed in universities' education departments. –  Feb 24 '17 at 05:02
  • Is there more context to the question? E.g. models of understanding around early childhood proportional reasoning may be different from post-secondary real analysis. – Benjamin Dickman Dec 24 '17 at 17:21
  • I strongly recommend review another "mental model" or cognitive process frameworks. Based in my experiences, I don't totally agree with Bloom's taxonomy because in mathematical practices different cognitive processes are activated and those could not approach to the Bloom's proposal. The question is why we don't use other taxonomy of mathematical processes. For instance, SOLO taxonomy or MATH taxonomy. My idea is to dig into these models and entail some of them in our practices. This decision depends of your goals and the context where you are teaching (e.g. elementary school or high school). – Carlos Torres Feb 15 '18 at 15:54

1 Answers1

1

I think that any response to this question would just be a matter of taste. It's hard to say anything objective in the way of one model being more useful than another. I would recommend abandoning the thought that there is a most useful model. Instead, read about these three models, and about any other models you find, looking only to understand why the authors decided that their model represents how math should be taught or learned. Then from this understanding, form your own model of how to teach mathematics. I think that you can safely disregard these models as immutable rules, but instead think of them only as scaffolding to build your own philosophy on teaching mathematics.

Something does need to be said in support of designing models like these in the first place, though. Teaching feels very natural to some people, and to these people models like these feel silly, like a formalization of how to eat a sandwich. But teaching doesn't come so naturally to everyone. Or at the very least not everyone has developed a coherent philosophy of how to teach yet. I think this is especially true of some early-career mathematics educators, or of math education students who have so far thought about teaching mathematics very little in their lives. Having models like these provide scaffolding, a jumping-off point, for people like this to begin developing their own thoughts on teaching. They provide a solid base to stand on while maturing as a mathematics teacher.

Mike Pierce
  • 4,845
  • 1
  • 20
  • 56