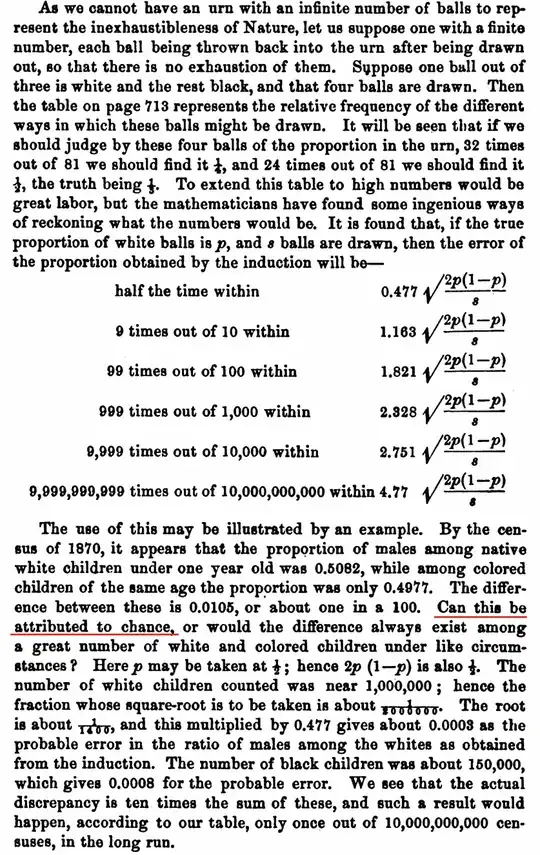6

In 1878, C. S. Peirce performed a calculation that (I think) would be better done using chi-squared testing — but Pearson hasn’t introduced that yet.

What exactly is Peirce doing here in the last sentence? Is it valid? almost valid? (When I did a chi-squared test, I got a different answer than he did.)

Peirce calculates the probability that a difference can be due to chance.

The first paragraph is straightforward enough. Where we would now say the probable error in the distribution of a sample is within +/- .6745 standard deviations, he has .477 * sqrt(2), and so on down his table.

In the next paragraph, he approximates p = 0.5 and then correctly calculates probable error on the two distributions.

But then what does he do in the last sentence?

(Once I figure that out, I’ll need to figure out if this was a common pre-Pearson approach.)

JPM
  • 171
  • 2

1 Answers1

1

It looks like he is saying the probable error of the difference between the two proportions is no more than the sum of the two probable errors, so $$d_1+d_2=0.0008+0.0003=0.0011$$ and that $$10(d_1+d_2)=0.011\approx 0.0105=\text{the actual discrepancy.}$$

Bjørn Kjos-Hanssen
  • 253
  • 1
  • 8