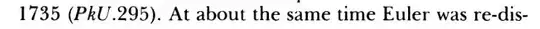7

Euclidean algorithm is an algorithm that produces the greatest common divisor of two integers. It was described by Euclid as early as in 300 BC.

On the other hand, the extended Euclidean algorithm extends his algorithm to express the greatest common divisor as an integer-linear combination of the two inputs.

Who came up with the extended Euclidean algorithm?

Conifold
  • 75,870
  • 5
  • 181
  • 284
Leaky Nun
  • 219
  • 1
  • 4
  • 2
    One does not need the extended Euclidean algorithm to derive the Bezout identity: the identity can be proved in other ways. For a homework assignment, I derived Bezout's identity in "math camp" (the Ross Mathematics Program) many years ago by looking at the set of linear combinations of the two given values. This is an existence proof, not computational and not using the Euclidean algorithm. Could you rewrite the title to this question? – Rory Daulton May 24 '18 at 09:21
  • @Rory Presuming that you refer to this method of deriving Bezout (or its variant using division with remainder vs subtraction) then it in fact does (implicitly) use the Euclidean algorithm. Further, it is not only an existence proof since it has an immediate constructive extension that leads to one form of the extended Euclidean algorithm.. – Bill Dubuque Jul 05 '18 at 14:07

2 Answers2

4

The earliest forms of the extended Euclidean algorithm are ancient, dating back to 5th-6th century A.D. work of Aryabhata - who described the Kuttaka ("pulverizer") algorithm for the more general problem of solving linear Diophantine equations $ ax + by = c$. It was independently rediscovered numerous times since, e.g. by Bachet in 1621, and Fermat and Wallis, and by Euler circa 1731.

Weil discusses this briefly in his book Number Theory: An Approach through History from Hammurapi to Legendre, excerpted below (from pp. 6-7) enter image description here enter image description here Euler's rediscovery is mentioned on pp. 176-77:

enter image description here enter image description here

It deserves to be more widely known that the algorithm is simpler to execute (and remember) if you are already familiar row-operations such as in Gaussian elimination / triangularization in linear algebra. See this MSE answer for a presentation from that viewpoint. This method eliminates the notoriously error-prone back-substitution in the more common presentation of the algorithm. Below is a worked example done this way, computing $\, \gcd(141,19),\, $ shown firstly in full equational form, and secondly in more concise tabular form. $$\rm\begin{eqnarray}[\![1]\!]\!\quad \color{#C00}{141}\!\ &=&\,\ \ \ 1&\cdot& 141\, +\ 0&\cdot& 19 \\ [\![2]\!]\quad\ \color{#C00}{19}\ &=&\,\ \ \ 0&\cdot& 141\, +\ 1&\cdot& 19 \\ \color{#940}{[\![1]\!]-7\,[\![2]\!]}\, \rightarrow\, [\![3]\!]\quad\ \ \ \color{#C00}{ 8}\ &=&\,\ \ \ 1&\cdot& 141\, -\ 7&\cdot& 19 \\ \color{#940}{[\![2]\!]-2\,[\![3]\!]}\,\rightarrow\,[\![4]\!]\quad\ \ \ \color{#C00}{3}\ &=&\, {-}2&\cdot& 141\, + 15&\cdot& 19 \\ \color{#940}{[\![3]\!]-3\,[\![4]\!]}\,\rightarrow\,[\![5]\!]\quad \color{#C00}{{-}1}\ &=&\,\ \ \ 7&\cdot& 141\, -\color{}{ 52}&\cdot& \color{}{19} \end{eqnarray}\qquad\qquad\qquad$$ $$\rm\begin{eqnarray} &&[\![1]\!]\quad \color{#C00}{141} &\ \ \ 1 &\quad\ \ 0 \\ &&[\![2]\!]\quad\ \color{#C00}{19} &\ \ \ 0 &\quad \ \ 1 \\ \color{#940}{[\![1]\!]-7\,[\![2]\!]}\,\rightarrow\,&&[\![3]\!]\quad\ \ \ \color{#C00}{ 8} &\ \ \ 1 &\ -7\\ \color{#940}{[\![2]\!]-2\,[\![3]\!]}\,\rightarrow\,&&[\![4]\!]\quad\ \ \ \color{#C00}{3} & -2 &\ \ \ \, 15 \\ \color{#940}{[\![3]\!]-3\,[\![4]\!]}\,\rightarrow\,&&[\![5]\!]\quad \color{#C00}{{-}1} &\ \ \ 7 & \, \color{}{{-}52} \end{eqnarray}\qquad\qquad\qquad\qquad\qquad\quad\ $$

One can optimize even further (e.g. see the fractional form below). It would be interesting to know who first presented the algorithm from this viewpoint. Likely it as at least a few centuries old.

It would take immense effort to write a good history of the extended Euclidean algorithm and related ideas, since it occurs in many different guises throughout mathematics, e.g. search on the following keywords: Hermite / Smith normal form, invariant factors, lattice basis reduction, continued fractions, Farey fractions / mediants, Stern-Brocot tree / diatomic sequence.

In fact even in recent times there are useful twists on the algorithm that are discovered, e.g. we can present the algorithm efficiently in fractional form using modular arithmetic, e.g. below I show how we can compute $\,1/117\equiv\color{#c00}{-72} \pmod{337}\ $ this way.

${\rm mod}\ 337\!:\,\ \dfrac{0}{337} \overset{\large\frown}\equiv \dfrac{1}{117} \overset{\large\frown}\equiv \dfrac{-3}{\color{#0a0}{-14}} \overset{\large\frown}\equiv \dfrac{-23}5 \overset{\large\frown}\equiv\color{#c00}{\dfrac{-72} {1}}.\,$ Equivalently, without fractions

$\qquad\quad \begin{array}{rrl} [\![1]\!]\!:\!\!\!& 337\,x\!\!\!&\equiv\ 0\\ [\![2]\!]\!:\!\!\!& 117\,x\!\!\!&\equiv\ 1\\ [\![1]\!]-3[\![2]\!]=:[\![3]\!]\!:\!\!\!& \color{#0a0}{{-}14}\,x\!\!\!&\equiv -3\\ [\![2]\!]+8[\![3]\!]=:[\![4]\!]\!:\!\!\!& 5\,x\!\!\! &\equiv -23\\ [\![3]\!]+3[\![4]\!]=:[\![5]\!]\!:\!\!\!& \color{#c00}1\, x\!\!\! &\equiv \color{#c00}{-72} \end{array}$

Bill Dubuque
  • 139
  • 1
  • 7
  • Weil's equating of Chinese Remainder Theorem with the Extended Euclidean Algorithm seems very anachronistic to me, especially since Sunzi's prescription for solving the system Weil gives bears no resemblance to EEA. I suspect even modern students would be stumped if asked to relate CRT to EEA without hints, and Sunzi did not even have the benefit of congruence notation. Aryabhata's "pulverizer" is warmer. – Conifold May 24 '18 at 08:20
  • @Conifold But Weil writes "if we leave China aside", so he may not intend that remark to apply to Sunzi. The later work in India (kuttaka) demonstrates knowledge of the simple equivalences (if modern students don't know these equivalences then the number theory course is lacking). "Congruence notation" is not needed to understand such equivalences (Weil uses it merely for the modern reader's convenience). – Bill Dubuque May 24 '18 at 21:01
  • @Conifold As for Sunzi, his lone example gives no clue whatsoever how he finds the auxiliary numbers $x \equiv 1 \pmod m,\ x\equiv 0 \pmod n$ so we don't know if he knew a general method. Usually this is done by EEA or equivalents (e.g. computing $,x\equiv n(n^{-1}\bmod m)$ using EEA for inversion). – Bill Dubuque May 24 '18 at 21:08
3

The path seems a bit deep, but here's a start, from wikipedia

The extended Euclidean algorithm was published by the English mathematician Nicholas Saunderson,[38] who attributed it to Roger Cotes as a method for computing continued fractions efficiently.[39]

Ref 38 is Saunderson, Nicholas (1740). The Elements of Algebra in Ten Books. PDF at this archive

Ref 39 is Tattersall, J. J. (2005). Elementary Number Theory in Nine Chapters. Cambridge: Cambridge University Press. ISBN 978-0-521-85014-8., pp. 72–76.

Mauro ALLEGRANZA
  • 14,569
  • 1
  • 36
  • 50
Carl Witthoft
  • 2,608
  • 12
  • 13