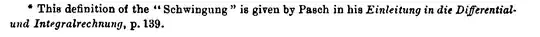2

I have two related questions:

  1. Who first defined the oscillation function (perhaps under a different name)?
  2. When did the switch from the phrase "saltus function"(*) to "oscillation function" happened?

Recall that given a topological space $X$, a metric space $M$, and a function $f:X\to M$, the oscillation function of $f$ is defined as:

$$\mathrm{osc}_\cdot(f):X\rightarrow[0,\infty],x\mapsto\mathrm{inf}\{\mathrm{diam}(f(U))|U\text{ is a nbdgd of } x\}$$

For what it's worth, Froda, in his 1929 thesis Sur la distribution des propriétés de voisinage des fonctions de variables réelles (https://eudml.org/doc/192780) attributes (p.23) the observation that the higher order oscillations stabilize to a 1905 paper by Denjoy (where this is used implicitly, Froda says as far as I can see) and a 1910 paper by Sierpinski.

(There are other, non-pointwise definitions, or else definitions in terms of the difference between limit superiors and limit inferiors also; these definitions are also admissible for the purposes of this question.)

(*): See e.g. Hobson's 1921 book The theory of Functions of a Real Variable and the Theory of Fourier's Series, Vol. I (2e) , p.291, or Blumberg's 1917 paper "Certain General Properties of Functions".

Finally, here is the OED definition of "saltus" (I hadn't heard of this word before):

enter image description here

(Oxford English Dictionary, s.v. “saltus (n.),” July 2023, https://doi.org/10.1093/OED/6909159924. )

In light of the definition of the word it seems more appropriate to call the function at hand the saltus function than the oscillation function (also keeping in mind the more commonly studied "BMO functions").

Alp Uzman
  • 347
  • 1
  • 7
  • Comment: a word related to saltus is used in saltatory conduction, in neuroscience – J. W. Tanner Sep 05 '22 at 17:44
  • 1
    @J.W.Tanner Interesting, thanks! – Alp Uzman Sep 05 '22 at 17:45
  • 1
    Another word related to saltus is somersault . It's not so common nowadays, but saltation can mean the act of leaping, jumping, or dancing. – kimchi lover Sep 05 '22 at 20:14
  • 1
    The word "saltus" was often used in the early 1900s literature in English (but "oscillation" was also used in this literature), and some authors made a distinction whereby one of the words was when the value of the function at the specified point is taken into account and the other word didn't (Hobson does this, for instance). My several comments to History of supremum with parameters gives some information about this topic and where to look. – Dave L Renfro Sep 05 '22 at 20:31
  • 1
    I looked in some older books I have and it seems "saltus" is less used in the early 1900s than I thought. Blumberg used it in many of his papers and published abstracts and Zbl reviews, which is probably why I thought it was used a lot in the early 1900s. Regarding Sierpinski's 1910 result, I believe this was rediscovered in: Lester Randolph Ford, Pointwise Discontinuous Functions, Master of Arts Thesis (under Earle Raymond Hedrick), University of Missouri (Columbia, Missouri), 1912, iii + 45 + 14 pages (see the last few pages). – Dave L Renfro Sep 06 '22 at 13:39
  • Incidentally, Ford published some results on the oscillation of a function a couple of years later in On the oscillation functions derived from a discontinuous function. Ford moved onto other areas of mathematics, and he's probably better known now (but this has only been the case in the past 2 or 3 decades) for Ford circles. (continued) – Dave L Renfro Sep 06 '22 at 13:56
  • Ford's Masters supervisor, Hedrick, published more in classical real analysis than Ford (whose paper I cited might be the only such paper, but I haven't looked into this), much of it mostly unknown today (for example, see the paper I cite here, which incidentally uses the word "oscillation"). – Dave L Renfro Sep 06 '22 at 13:56
  • @DaveLRenfro Thank you for the references; I had seen some of your related comments on M.SE which were also helpful. I will need some time to look more into the papers, but it seems your best bet tentatively is Ascoli 1875 for the origin of the oscillation function, is this an accurate statement? – Alp Uzman Sep 06 '22 at 19:13
  • 1
    @Alp Uzman: For oscillation defined pointwise, 1875 is probably appropriate. For oscillation in an interval, it's not as clear. Hankel certainly dealt with oscillation in an interval in his 1870 memoir, and I think it appears, at least implicitly in Riemann's 1854 thesis on the Riemann integral and Fourier series. And Cauchy dealt with pointwise lim-inf and lim-sup, although probably not their difference (pointwise or in an interval). (continued) – Dave L Renfro Sep 06 '22 at 19:37
  • 1
    Finally, if we're talking about the oscillation explicitly as a function, this probably didn't occur until Baire (certainly by 1899; maybe in a C. R. Acad. Sci. Paris note a year or two earlier). But you'd want to carefully look through Dini's 1878 book in any case, as much in that book has not been all that thoroughly documented (example), except stuff that directly leads to well-studied areas such as the precursor work to Lebesgue integration and Dini derivates (although even this hardly mentions what Dini actually did with his derivates). – Dave L Renfro Sep 06 '22 at 19:42
  • @DaveLRenfro Thank you so much. Like I said I will need some time to reference chase. – Alp Uzman Sep 06 '22 at 19:44
  • Is OED paywalled? Can you add a link? – Mauricio Jan 30 '24 at 16:30

2 Answers2

2

Searching Google Books often leads to useful results. I searched your keywords as "oscillating function" "saltus" Hobson. This leads to the same book "The Theory of Functions of a Real Variable and the Theory of Fourier's Series Volume 1, By Ernest William Hobson, 1921"

On page 284, Hobson has a footnote with a asterisk on oscillation. In other books, Hobson is credited with saltus.

"enter image description here

So it seems Schwingung was translated to oscillation. You will have scavenge German literature. DeepL is an excellent free machine translator. Saltus itself is inspired by German Sprung most likely by the author himself (pg 283).

AChem
  • 4,034
  • 1
  • 16
  • 32
  • 1
    I located Pasch' book and ran some OCR. I could not find "Schwingung" (not on page 139 or anywhere), although the more standard "Schwankung" is there (p. 17). Pasch cites Riemann and Luroth for the latter term. – Sam Sanders Sep 06 '22 at 08:39
2

The notation is a bit harsh, but Ascoli defines 'oscillazione' in the following paper (p. 867, paragraph 6; see also p. 869, at the top, for a reference to Riemann, Über die Darstellbarkeit einer Function durch eine trigonometrische Reihe) and formulates a version of the Vitali-Lebesgue theorem using this notion.

Giulio Ascoli, Sul concetto di integrale definito, Atti della Reale Accademia dei Lincei. Classe di Scienze Fisiche, Matematiche e Naturali 2 (1875), no. 2, 862-872.

user6530
  • 3,870
  • 1
  • 15
  • 32
Sam Sanders
  • 213
  • 1
  • 6
  • It must be added that Ascoli himself complained in Sulla definizione di integrale (1895) that his note, inspired by Riemann's research, had gone completely unnoticed, and that many of his ideas were later attributed to other authors. However, it must be said that the notations used by Ascoli were really too complicated to be appreciated. – user6530 Jan 30 '24 at 17:48
  • The notation is indeed harsh, and I would add that Ascoli's results are not in their final/simplest form. – Sam Sanders Jan 31 '24 at 11:02