While in the present day the word "organic" has connotations of "natural" and "holistic", back in Newton's day it was much closer to the Greek word oργανoν (organon: tool, instrument).
For an exploration of organic methods and their place in 17th century geometry I recommend Guicciardini, Isaac Newton on Mathematical Certainty and Method.
From pg 6:
Another line of research concerned the so-called organic description
(or generation) of curves. This was an important topic, since in order
to determine the point of intersection of curves in the construction
of geometrical solutions, it was natural to think of the curves as
generated by a continuous motion driven by some instrument (an
oργανoν). It is the continuity of the motion generating the curves
that guarantees a point of intersection can be located exactly.
Descartes had devised several mechanisms for generating curves. In De
Organica Conicarum Sectionum in Plano Descriptione Tractatus (1646),
which Newton read in Exercitationum Mathematicarum (1657), van
Schooten had presented several mechanisms for generating conic
sections. This research field was connected with practical
applications, for instance, lens grinding and sundial design, but it
was also sanctioned by classical tradition and motivated the highly
abstract needs underlined by Descartes. Newton was able to devise a
mechanism for generating conics and to extend it to higher-order
curves.
One theme found throughout the book is Newton's criticism of "speculative" methods such as Cartesian analysis, and the definition of conics as planar sections of a cone. Philosophically he much preferred the mechanical (organic).
From pgs 106-107:
[...] Newton criticized the lack of elegance and ease in Cartesian
analysis of indeterminate problems and believed Cartesian synthesis
was based on “spurious” postulates: point-wise constructions, motion
of curves, construction with threads, and intersection of cone and
plane (barren speculation). He favored expressing the contents of
known and unknown segments that have a given ratio to one another, and
using projective properties to compose the locus by organic
descriptions based on acceptable postulates, namely, rotating rulers.
Nevertheless, Newton was a master in Cartesian algebra, the “common
analysis of the moderns,” and when he had to deal with a challenging
problem, the classification of cubic curves, he made use of algebraic
techniques that were at odds with his program of restoration of
ancient analysis.
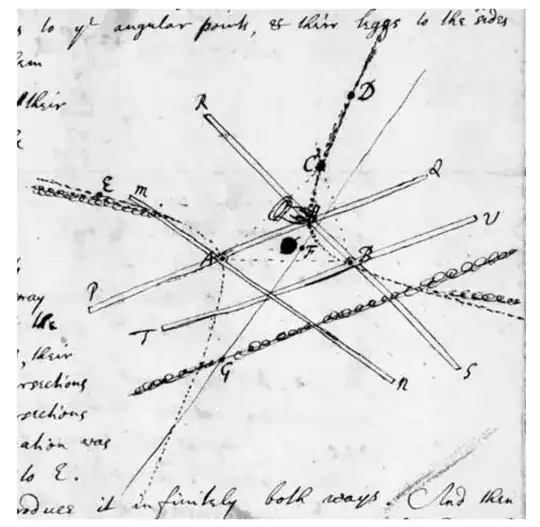
The book describes many organic mechanisms for generating curves. Newton invented a mechanism for determining tangents, and one that could be used to draw the conic defined by five points $A,B,C,D,E$ (pg 94, letter to John Collins, 1672,see below).