When I read Dickson's History Of The Theory Of Numbers Vol-2, I found that there seems to be a mistake in the approximation of partition numbers p(200). For this reason, I found the original text according to the literature. In the original text, the theorem gives the asymptotic formula of partition number.
$$p(n)\sim\sum^v_{q=1}A_q\phi_q+\mathcal{o}\left(n^{-\frac{1}{4}}\right)$$
where
\begin{matrix} \begin{array}{ll} A_1=1&A_2=\cos(n\pi)\\ A_3=2\cos\left(\frac{2}{3}n\pi-\frac{\pi}{18}\right)& A_4=2\cos\left(\frac{1}{2}n\pi-\frac{\pi}{8}\right)\\ A_5=2\cos\left(\frac{2}{5}n\pi-\frac{\pi}{5}\right)+2\cos\left(\frac{4}{5}n\pi\right)\qquad&A_6=2\cos\left(\frac{1}{3}n\pi-\frac{5\pi}{18}\right)\\ \end{array}\\ \begin{array}{l} A_7=2\cos\left(\frac{2}{7}n\pi-\frac{5\pi}{14}\right)+2\cos\left(\frac{4}{7}n\pi-\frac{\pi}{14}\right)+2\cos\left(\frac{6}{7}n\pi+\frac{\pi}{14}\right)\qquad\\ A_8=2\cos\left(\frac{1}{4}n\pi-\frac{7\pi}{16}\right)+2\cos\left(\frac{3}{4}n\pi-\frac{\pi}{16}\right)\\ \end{array} \end{matrix}
\begin{align*} \phi_q&=\dfrac{\sqrt{q}}{2\pi\sqrt{2}}\dfrac{\mathrm{d}}{\mathrm{d}n}\left(\dfrac{\exp\left(\frac{C\lambda_n}{q}\right)}{\lambda_n}\right)\\ &=\dfrac{\sqrt{q}}{2\pi\sqrt{2}}\dfrac{\mathrm{d}}{\mathrm{d}n}\left(\dfrac{\exp\left(\pi\sqrt{\frac{2}{3}}\cdot\frac{1}{q}\cdot\sqrt{\frac{1}{n}-\frac{1}{24}}\,\right)}{\sqrt{\frac{1}{n}-\frac{1}{24}}}\right)\\ &=\dfrac{\sqrt{q}}{2\pi\sqrt{2}}\dfrac{\mathrm{d}}{\mathrm{d}n}\left(\dfrac{\exp\left(\frac{\pi}{q}\sqrt{\frac{2}{3}\left(\frac{1}{n}-\frac{1}{24}\right)}\,\right)}{\sqrt{\frac{1}{n}-\frac{1}{24}}}\right)\\ \end{align*}
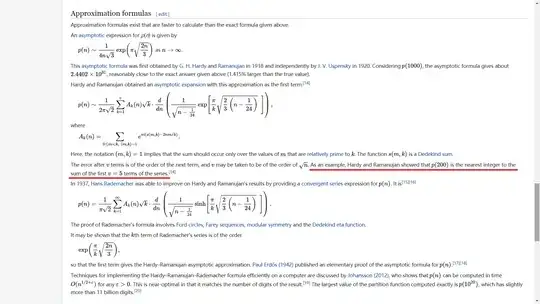
In the original text, the first six terms of series were used to calculate p(100), and the first eight terms of series were used to calculate p(200). But Wikipedia[2] says the first five terms of the series are used to calculate p(200). However, in the process of calculating p(200), are some values marked in red incorrect?
\begin{align*} A_1\phi_1(200)&=\dfrac{1}{2\pi\sqrt{2}}\left.\left\{\dfrac{\mathrm{d}}{\mathrm{d}n}\left(\dfrac{\exp\left(\pi\sqrt{\frac{2}{3}\left(\frac{1}{n}-\frac{1}{24}\right)}\,\right)}{\sqrt{\frac{1}{n}-\frac{1}{24}}}\right)\right\}\right|_{n=200}\\ &\approx3972998993185.896\\ A_2\phi_2(200)&=\dfrac{1}{2\pi}\left.\left\{\cos\left(n\pi\right)\dfrac{\mathrm{d}}{\mathrm{d}n}\left(\dfrac{\exp\left(\frac{\pi}{2}\sqrt{\frac{2}{3}\left(\frac{1}{n}-\frac{1}{24}\right)}\,\right)}{\sqrt{\frac{1}{n}-\frac{1}{24}}}\right)\right\}\right|_{n=200}\\ &\approx36282.978\\ \end{align*}
\begin{align*} &&A_3\phi_3(200)&\approx-87.584&&A_4\phi_4(200)\approx5.147&&A_5\phi_5(200)\approx1.424\\ &&A_6\phi_6(200)&\approx0.071&&A_7\phi_7(200)=0&&A_8\phi_8(200)\approx0.044\\ \end{align*}
\begin{align*} \text{My Vertical Calculation}&\qquad&\text{Original Vertical Calculation}\\ \begin{array}{r} 3972998993185.896\\ +\,\,36282.978\\ -\,\,87.584\\ +\,\,5.147\\ +\,\,1.424\\ +\,\,0.071\\ +\,0\qquad\\ +\,\,0.044\\ \hline 3972999029387.975 \end{array}&\qquad& \begin{array}{r} 3972998993185.896\\ +\,\,36282.978\\ -\,\,{\color{red}{87.\boxed{555}}}\\ +\,\,5.147\\ +\,\,1.424\\ +\,\,0.071\\ +\,0\qquad\\ +\,\,{\color{red}{0.\boxed{043}}}\\ \hline 3972999029388.004 \end{array} \end{align*}
Finally, I searched the results (3972999029387.975) in Google and found the lecture notes [5].
[1] History Of The Theory Of Numbers Vol-2 (Leonard Eugene Dickson)
https://archive.org/details/HistoryOfTheTheoryOfNumbersVolII/page/n187/mode/2up
[2] Partition function [Wikipedia]
https://en.wikipedia.org/wiki/Partition_function_(number_theory)#Approximation_formulas
[3] Asymptotic Formulæ In Combinatory Analysis (G. H. Hardy & S. Ramanujan) [Original edition]
[4] Asymptotic Formulæ In Combinatory Analysis (G. H. Hardy & S. Ramanujan) [Reset edition BY LaTeX]
http://ramanujan.sirinudi.org/Volumes/published/ram36.pdf
[5] Lectures on Integer Partitions (Herbert S. Wilf)