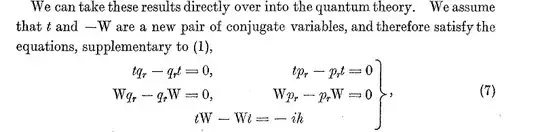2

Heisenberg already in 1927 quotes this equation as a "known equation".1

enter image description here

Then what is the origin of it? And what is its further history of it, ending in its death?

1 Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik, Zeits. f. Phys. 43 172 1927. (p.8. in pdf in English),

mma
  • 139
  • 5
  • 1
    It seems to me that is's nor a bluff! Thanks for your help, finally, I've found this equation in Dirac's Relativity quantum mechanics with an application to Compton scattering Proc. R. Soc. Lond. A 1926 111, 405-423. This is among eqs. (7). So I think that this is the origin of this equation. – mma Feb 23 '20 at 19:24
  • Be equally interesting to discuss the fact that the difference is purely imaginary. – Carl Witthoft Feb 24 '20 at 15:08
  • 1
    @CarlWitthoft You mean that in general, the commutator of two canonocal conjugate quantities is always anti-self-adjoint. The root of this is in Stone's theorem. This theorem states that there is a one-to-one correspondence between anti-self-adjoint operators and (strongly continuous) one-parameter unitary groups. (see https://en.wikipedia.org/wiki/Stone%E2%80%93von_Neumann_theorem#Uniqueness_of_representation) – mma Feb 26 '20 at 07:39

2 Answers2

3

Since you do not explain what $E$ and $t$ mean, I suppose that this is the equation written by M. Born and P. Jordan, Zur Quantenmechanik, Z. Phys. 34 (1925), Eq. 38, few weeks after Heisenberg published his first version of Quantum Mechanics. Of course, by 1927 it was already well-known. Development was very fast in this area.

Alexandre Eremenko
  • 48,930
  • 3
  • 80
  • 177
  • Eq 38 is $\boldsymbol{pq}-\boldsymbol{qp}=\frac{h}{2\pi i}$, not $\boldsymbol {Et}-\boldsymbol {tE}=\frac{h}{2\pi i}$. The difference is that $\boldsymbol{q}$ is an existing self-adjoint , bounded operator, but $\boldsymbol{t}$ isn';t. – mma Feb 22 '20 at 18:36
  • 1
    @mma This is an absurdly narrow and, as you find, meaningless misinterpretation of the sound and useful relation. It was actually discovered/properly understood by Mandelstam and Tamm in 1945. One may always dismiss something if properly garbled and misconstrued. – Cosmas Zachos Feb 23 '20 at 14:12
1

As a comment (deleted since) pointed out, the source is mentioneed in in §5.4, p. 140 of Jammer, The Philosophy of Quantum Mechanics. It is P. A. M. Dirac, Relativity quantum mechanics with an application to Compton scattering Proc. R. Soc. Lond. A 1926 111, 405-423. The equation in question is among eqs. (7) (the energy operator is denoted here by $W$):

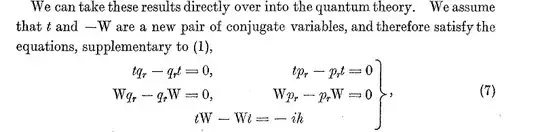
enter image description here

This formula was proved to be senseless by Wolfgang Pauli, in Handbuch der Physik, zweite Auflage, Band XXIV, Ersten Teil - Quantentheorie, Springer-Verlag Berlin Heidelberg GmbH, 1933, p 140:

enter image description here

The English translation of the marked sentence can be found in Fundamental Questions in Quantum Mechanics, p. 266 as

We conclude that the introduction of an operator t must fundamentally be abandoned and that the time t in quantum mechanics has to be regarded as an ordinary number (c-number')

mma
  • 139
  • 5