3

I'm having difficulties to understand how does this circuit work:

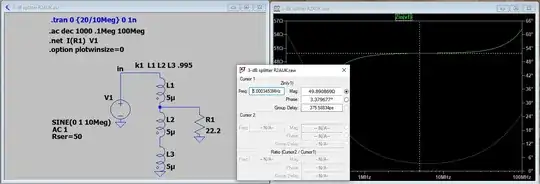
enter image description here

Apparently T1 is a regular 50 Ohm to 22.2 Ohm autotransformer. Turns ratio 2:3 gives a 0.66**2 impedance converation. Since the load is two 50 Ohm ports in parallel, the total load impedance will be 25 Ohm. In other words T1 is just for impedance matching.

From what I know T2 and R are needed for isolation of port 2 and port 3. This is the part I don't quite understand. What happens when the circuit is used as a splitter? And what happens when it's used as a combiner? What prevent the current just to flow from port 3 to port 2 through R?

Could you please explain it?

Marcus Müller
  • 15,910
  • 23
  • 45
Aleksander Alekseev - R2AUK
  • 4,272
  • 15
  • 52
  • 2
    That's a very specific hybrid (what the author of the article claims to be a 0°/180° hybrid). Usually, the primary/secondary side windings are not in a relationship of 3:2 but $\sqrt2:1$, so maybe this just "empirically" works well enough for them. It's certainly not an optimal design. So, not quite sure there can be reasonable explanation - this is not what you should be building when building a hybrid splitter. – Marcus Müller May 30 '20 at 15:47
  • 4
    Don't know whether this link works for you, but a proper RF design book is probably a better source than random hams on the internet. (Oh, the irony.) – Marcus Müller May 30 '20 at 15:48
  • @MarcusMüller I'd love to have that book! But I didn't see anything like Aleksander's circuit on the pages we are allowed to view. – Mike Waters May 30 '20 at 18:20

1 Answers1

4

SPICE modeling shows that replacing T2 and R with a 22.2-$\Omega$ resistor, the impedance looking into T1 is indeed 50-$\Omega$, as expected:

enter image description here

Similarly, replacing the 50-$\Omega$ generator and T1 with a 25-$\Omega$ generator shows that the impedance looking into T2 is 25-$\Omega$:

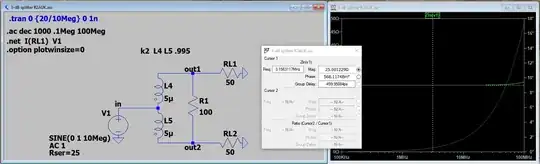
enter image description here

This is a result of the electrical symmetry about a "virtual ground" established by the junction of the two windings of T2 and the "midpoint" of the 100-$\Omega$ resistor. Thus, each side of T2 is terminated by two paralleled 50-$\Omega$ resistances, or 25-$\Omega$, matching the generator.

Note, though, that the composite circuit presents a slight mismatch of 56-$\Omega$ to the generator:

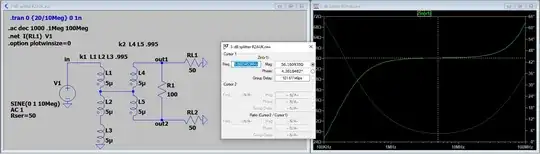
enter image description here

This is a result of the difference between the 22.2-$\Omega$ transformation of T1 and the 25-$\Omega$ input to T2. That is, 50*(25/22.2)=56-$\Omega$.

The isolation between the two output ports can be measured by driving one of the output ports, terminating the "input" port in its characteristic impedance and measuring the response at the other output port:

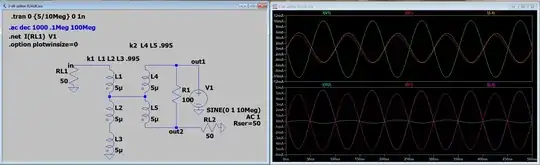
![enter image description here

As shown the isolation between the two output ports is better than 30-dB as long as all ports are terminated in 50-$\Omega$. The strong coupling between the windings of T2 means that equal but opposite currents flow with respect to their connections to R1. Whereas the driving current I(V1) is split between L4 and R1, the current in L5 cancels the current flowing into node out2 from R1, effectively isolating it from node out1.

[Note: in LTSpice convention, I(V1), I(R1) and I(L4) are all leaving node out1, while I(L5), I(R1) and I(RL2) are all entering node out2.]

Brian K1LI
  • 7,838
  • 10
  • 33
  • Many thanks for the explanation. However this doesn't really answers my question... What interests me is if T2-R part really provides isolation between ports 2 and 3 and if so how does it work. – Aleksander Alekseev - R2AUK May 30 '20 at 16:58
  • @AleksanderAlekseev-R2AUK Apologies; I hope my last edit addressed the isolation question. – Brian K1LI May 31 '20 at 13:37
  • Many thanks once again. But I believe this explanation is not quite right. The model shows that changing R1 doesn't affect the impedance of the right part of the circuit. This is not surprising - because of the symmetry the voltage on both sides of R1 is the same, there is no current flowing through it. Apparently it's needed only as a current path in isolation scenario, not for impedance matching as the answer implies. There is one thing that I still can't understand though. Why the best isolation is achied when R1 is about 100 Ohm? – Aleksander Alekseev - R2AUK May 31 '20 at 13:58
  • 1
    After playing with the model a little I figured this out. From out1 point of view L4-L5 transformer would look as 100 Ohm = 25 Ohm * 4 (since the turns ratio is 2:1) if out2 would be ground. We choose R1 so that it's impedance is equal to L4-L5 thus currents cancel each other in out2 point. Since no current is flowing through RL2, out2 potencial is about 0V and thus L4-L5 impedance is indeed 100 Ohm. – Aleksander Alekseev - R2AUK May 31 '20 at 14:41
  • It's also interesting to observe the effect of the value of R1 on the isolation between the two output ports. Terminating *out1* in, e.g., $25\Omega$ or $100\Omega$, it's clear that setting R1 to $100\Omega$ produces the least disturbance in the current flowing in RL2. – Brian K1LI May 31 '20 at 15:53