How to create when possible a rectangle in polygons with holes

Question

I did not find a similar question on this site. Is there a way to automatically create a rectangular polygon of 500 square meters inside another polygon with rings using QGIS? (I have 28,000 polygons with rings)

I specify my question: my work consists of studying a built-up area (see A) .

In some cases, the land can still accommodate construction. To find these situations, I made a buffer around the frames with a setback

(see B ),

I cut these buffers out of the land

(see C )

The objects obtained (C) have a total area which is not relevant to take into account its building potential (because of the holes). The idea is to insert, when possible, in each object of C, a rectangular piece of land with a given area (for example: 500 m² , cf red rectangular).

Can you give me a lead?

Answer 1

Create random points in each plot, buffer them, create rectangles from the buffers using st_expand, select the rectangles within each plot that doesnt intersect any building:

--Create n random points in each plot
create table pointsinplot as
with cte as (
select (st_dump(st_generatepoints(geom, 10000))).geom from
(select distinct p.geom from plot p
left join
building b
on st_within(st_centroid(b.geom), p.geom)) sub
)
select row_number() over() as rnum, cte.geom from cte
left join building b
on st_intersects(cte.geom, b.geom)
where b.geom is null --no points allowed inside the buildings
--Buffer each point, expand the buffers into a rectangle by random x an y factors and rotate by random radians
create table randomrectangles as
with cte as (
select st_expand(st_buffer(geom, 2),floor(random() * 10 + 1)::int,floor(random() * 10 + 1)::int) geom from public.pointsinplot
)
select row_number() over() as rnum, st_rotate(geom, random()2pi(), st_centroid(geom)) geom from cte
--Find the rectangles within plots, not intersecting the buildings
drop table if exists potential_sites;
create table potential_sites as
with cte as (
select plotid, row_number() over() as rnum, r.geom from randomrectangles r
join plot p
on st_within(r.geom, p.geom)
)
select cte.plotid, cte.rnum, cte.geom, st_area(cte.geom) from cte
left join building b
on st_intersects(cte.geom, b.geom)
where b.geom is null
--Find largest rectangle per plot
SELECT DISTINCT ON (plotid)
       plotid, geom
FROM   potential_sites
ORDER  BY plotid, st_area(geom) DESC;

Answer 2

Principles: what you can expect from this solution

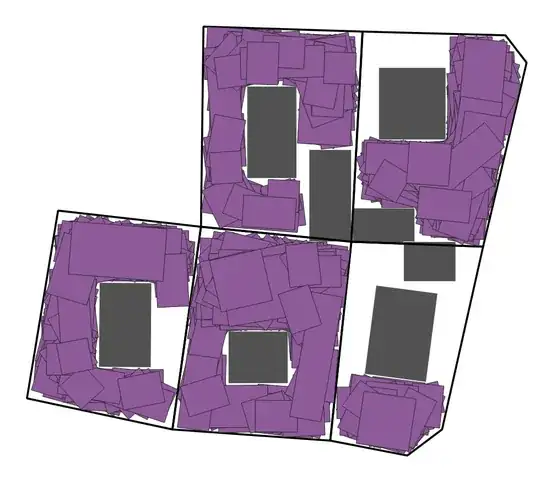
This solution is a heuristic approach. It returns parcels where for sure a 500 sqm rectangle can be placed as well as other "candidate" parcels with a high probability that this will be possible, but that have to be checked manually. See screenshot:

Result: initial building (gray) with buffer (wihte) and remaining parcel (red). The two possible buildings with 500sqm (hatched in gray with black outline). The lower one is completely inside the parcel, thus one that automatically is recognized as a solution; the upper one is not completely, but almost inside the parcel (just 3% of its area outside the parcel) - so a candidate to take into consideration - and indeed, shifting the polygon a bit, it would fall completely inside the parcel:

The solution step by step

1. Get the parcel that remains when cutting out the buffered buildings (using Difference tool).

2. Cut narrow connecting "corridors" between the main shapes by buffering with a negative value of lets say -5 m, then apply the inverse, positive value for buffering: 5 m.

Left: building 8gray), buffer (yellow), remaining parcel (red); middle: remaining parcel (red), negative buffer (blue); right: remaining parcel (outlined in red), negative buffer (outlined in blue), the two resulting parcels we will use from now on (solid orange):

3. Convert from Multipart to single parts and add a unique id (here: fid) to the result.

4. Use Menu Processing / Toolbox / Minimum bounding geometry and create the Minimum oriented rectangle, based on the fid to get a separate box for each feature.

5. Scale the polygons from step 4 with a scale factor so that they are the size you want (500 square meters, in your case). The scale factor is the square root of (500 divided by the area of the polygon) (pseudocode).

   The parcels from above (orange), the minimum oriented rectangle from step 4 (blue) and these rectangles scaled down to 500 sqm (red) - here using Geometry generator:

   The expression 1 (see at the bottom) returns the Minimum oriented rectangle, scaled to an area of 500 sqm, with the same centroid.

6. Now calculate the intersection of the scaled polygon (step 5) with the parcel polygon from step 3. If the scaled 500 sqm polygon is completely within the parcel, the intersection is the same as the output of step 5. If it is not completely within it, some parts are cut away. Thus now calculate the area of this intersection with the expression 2 from below (an extension of expression 1) creating a new attribute field with Field calculator.

7. Now select all features where the field calculated in step 6 is near the value of 500 sqm. Ideally, we could just look for the vlaues that are exactly 500 sqm. But we should subtract a ceratain tolerance threshold to account for the fact that sometimes, shifting the scaled polygon inside the parcel could result in a larger interesection. So based on your needs and the type of the data you have, select all values in a certain range (like 450 to 500).

Expressions

Expression 1

 with_variable(
     'scale',
     sqrt (500/$area),
     make_rectangle_3points(
         project (
             centroid ($geometry),
             @scale*length (make_line (point_n ($geometry, 1), centroid ($geometry))),
             azimuth (point_n ($geometry, 1), centroid ($geometry))
         ),
         project (
             centroid ($geometry),
             @scale*length (make_line (point_n ($geometry, 2), centroid ($geometry))),
             azimuth (point_n ($geometry, 2), centroid ($geometry))
         ),
         project (
             centroid ($geometry),
             @scale*length (make_line (point_n ($geometry, 2), centroid ($geometry))),
             azimuth (point_n ($geometry, 3), centroid ($geometry))
         )
     )
 )

Expression 2

 area (
     intersection (
         with_variable(
             'scale',
             sqrt (5000/area($geometry)),
             make_rectangle_3points(
                 project (
                     centroid ($geometry),
                     @scale*length (make_line (point_n ($geometry, 1), centroid ($geometry))),
                     azimuth (point_n ($geometry, 1), centroid ($geometry))
                 ),
                 project (
                     centroid ($geometry),
                     @scale*length (make_line (point_n ($geometry, 2), centroid ($geometry))),
                     azimuth (point_n ($geometry, 2), centroid ($geometry))
                 ),
                 project (
                     centroid ($geometry),
                     @scale*length (make_line (point_n ($geometry, 2), centroid ($geometry))),
                     azimuth (point_n ($geometry, 3), centroid ($geometry))
                 )
             )
         ),
         overlay_nearest ('parcel',$geometry)[0]
     )
 )