Obtaining area modified by altitude using PostGIS

Question

How to change area calculation, making use of altitude?

I am supposing that at Z=0 is the default (geoid surface) for PostGIS. So we can expect different area when Z=800 or Z=8000... But, using the tests below was not possible to obtain different results.

SELECT ST_Area(geom) as spheric_area,
       ST_Area(geom_z) as spheric_area_z, -- ST_3DArea(geom_z) is error
       ST_Area(geom,true) as area,
       ST_Area(geom_z,true) as area_z
FROM (                    
   SELECT ST_GeomFromText(
           'POLYGON Z((-46.6342 -23.55057 800.0,-46.6342 -23.5492 800.0,-46.6328 -23.5492 800.0,-46.6328 -23.55057 800.0,-46.6342 -23.55057 800.0))',
           4326
          ),
          ST_GeomFromText(
           'POLYGON((-46.6342 -23.55057,-46.6342 -23.5492,-46.6328 -23.5492,-46.6328 -23.55057,-46.6342 -23.55057))',
           4326
          )
) t1(geom_z,geom);

spheric_area	spheric_area_z	area	area_z
1.917999999997526e-06	1.917999999997526e-06	21688.81550103426	21688.81550103426

---

((edit after @TimothyDalton suggestion))

Try also ST_3DArea

CREATE EXTENSION IF NOT EXISTS postgis_sfcgal;
SELECT ST_3DArea( geom_z) as area3d_z,
       ST_3DArea( ST_Transform(geom_z,'+proj=isea') ) as area3d_z_isea,
       ST_IsPlanar(geom_z)
FROM (

   SELECT ST_GeomFromText(
           'POLYGON Z((-46.6342 -23.55057 800.0,-46.6342 -23.5492 800.0,-46.6328 -23.5492 800.0,-46.6328 -23.55057 800.0,-46.6342 -23.55057 800.0))',
           4326
          )
) t1(geom_z);

Results: all same as ordinary ST_Area(),

• area3d_z = 1.917999999997526e-06
• area3d_z_isea = 21788.3 (not changes even even increasing altitude to 8000). Other projections (ex. Mercator or Albers) also not changes with altitude.
• It is a "planar geometry" (st_isplanar = t), so was expected no problem.

---

Notes for @jbalk and other comments

• I am supposing that we can confirm theory with PostGIS: area increase when altitude increase (Earth radius).
  

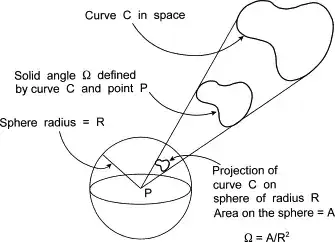
• The adoption of SRID 4326 (pure WGS84 with no projection) is to fix the solid angle (area in steradians), so the metric area "must" (hypothesis) to increase with Z.

Answer 1

St_3dArea will not work for this experiment. It uses a defined spheroid of the earth surface, so it won't work for areas at an altitude above the surface of the spheroid.

I did a little experimentation and came up with some functions that will allow you to find area at altitude.

First, you need a function to find the distance between points on the spheroid. I chose the haversine formula, and I found a function on github that I modified:

--Haversine formula for geodistance in km
drop function public.geodistance_km;
CREATE OR REPLACE FUNCTION public.geodistance_km(alat double precision, alng double precision, blat double precision, blng double precision, earthdia double precision default 12756)
  RETURNS double precision AS
$BODY$
SELECT asin(
  sqrt(
    sin(radians($3-$1)/2)^2 +
    sin(radians($4-$2)/2)^2 *
    cos(radians($1)) *
    cos(radians($3))
  )
) * $5 AS distance;
--earthdia use 2 * 6378 = 12756 for KM and 2 * 3963 = 7926 for MI
$BODY$
  LANGUAGE sql IMMUTABLE
  COST 100;

Then you need a function to find area at altitude. This function uses the geodistance function above to find the ratio of the geodistance on the ground and geodistance at altitude between 2 points from the input polygon. It does this by increasing the earth radius by the provided elevation (in KM):

--find earth radius at latitude of 1st point in geometry
--altitude is in kilometers!!
--multiply the area of the polygon by the ratio geodistance at altitude/geodistance on ground of the 1st and Mid points of the geometry
create or replace function areakm_at_altitude(geom geometry, alt double precision)
returns double precision  as
$$
with points as 
    (select 
        st_pointn(st_exteriorring($1),1) as p1, 
        st_pointn(st_exteriorring($1),
        (st_numpoints(st_exteriorring($1))/2)::int) as p2
    ),
earth_rad as 
    (select 
        sqrt(
            (((6378137.0^2) * cos(st_y(st_pointn(st_exteriorring($1),1))))^2 + ((6356752.3142^2) * sin(st_y(st_pointn(st_exteriorring($1),1))))^2)/
                ((6378137.0 * cos(st_y(st_pointn(st_exteriorring($1),1))))^2 + (6356752.3142 * sin(st_y(st_pointn(st_exteriorring($1),1))))^2)
            )/1000 as erad
    )
select 
    st_area($1::geography)/1000 * 
        geodistance_km(st_y((select p1 from points)), st_x((select p1 from points)), st_y((select p2 from points)), st_x((select p2 from points)), (select erad from earth_rad) + $2)/
        geodistance_km(st_y((select p1 from points)), st_x((select p1 from points)), st_y((select p2 from points)), st_x((select p2 from points)), (select erad from earth_rad));
$$ language sql immutable;

When I test this against the st_area function with geography casting, I get the same area at altitude 0:

select st_area(geom::geography)/1000 as st_area_km, areakm_at_altitude(geom, 0) from test_table where id = 19;

And, as expected, the area increases as you increase the altitude:

select st_area(geom::geography)/1000 as st_area_km, areakm_at_altitude(geom, 10) from test_table where id = 19;

earth radius equation came from here https://en.wikipedia.org/wiki/Earth_radius

---

Sample data:

DROP TABLE test_table;
CREATE TABLE test_table AS
 SELECT 1 AS id, 0.0::float AS altitude,
        'POLYGON'::text AS gtype,
        ST_GeomFromText(
         'POLYGON((-46.6342 -23.55057,-46.6342 -23.5492,-46.6328 -23.5492,-46.6328 -23.55057,-46.6342 -23.55057))',
         4326
       ) AS geom
UNION ALL
SELECT 2, 800.0, 'POLYGON Z', ST_GeomFromText(
   'POLYGON Z((-46.6342 -23.55057 800.0,-46.6342 -23.5492 800.0,-46.6328 -23.5492 800.0,-46.6328 -23.55057 800.0,-46.6342 -23.55057 800.0))',
   4326
 )
UNION ALL
SELECT 3, 8000.0, 'POLYGON Z', ST_GeomFromText(
    'POLYGON Z((-46.6342 -23.55057 8000.0,-46.6342 -23.5492 8000.0,-46.6328 -23.5492 8000.0,-46.6328 -23.55057 8000.0,-46.6342 -23.55057 8000.0))',
    4326
 )
;
-- Illustrating areakm_at_altitude() function:
SELECT id, altitude, st_area(geom::geography)/1000 as st_area_km,
       areakm_at_altitude(geom, altitude) 
FROM test_table;
-- Demonstrating no gtype effect, on constant altitude:
SELECT id, altitude, gtype, st_area(geom::geography)/1000 as st_area_km,
       areakm_at_altitude(geom, 10) 
FROM test_table;