Denote respectively rA and rB the reserve of Token A and Token B. Let f = 1 - fee (i.e. 0.997) and x be the input amount. Then the price function of Uniswap v2 for a pair (A, B) is
P(x) = (rB * x * f)/(rA + x * f)
This answer explains well how the source code computes it: the computation is based upon the preservation of the "constant product formula": rA * rB = k, where k is a constant. In other word, the product of the new reservers is the same as the old: rA' * rB' = rA * rB = k. But this seems to contradict the documentation of Uniswap v2 which says that
In practice, Uniswap applies a 0.30% fee to trades, which is added to reserves. As a result, each trade actually increases k.
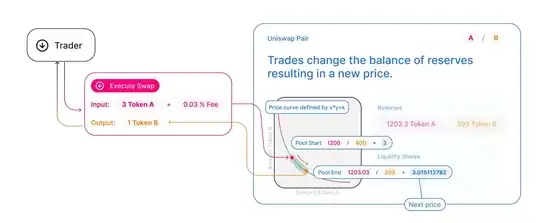
Moreover, the answer seems to suggest that the new reserves are rA' = rA + x * f and rB' = rB - P(x). I was rather confused when I have seen the diagram below from the documentation.
Here are my questions:
- If k actually increase at each trade, then why the price is computed in such a way (i.e. based on preservation of k) ?
- What should be the value of rA' on the diagram? Let x = 3, rA = 1200, then by the computation above, rA' = rA + x * f < 1203. It looks like that the illustration has multiple errors:
- It says that the fee is 0.03%, but it should be 0.3%
- It doesn't agree whether rA' is 1203.03 or 1203.3. But both are wrong either way.
- What the "price" in blue on the diagram actually means ? (why it doesn't use P(x) ?)