19

enter image description here

enter image description here

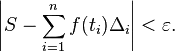
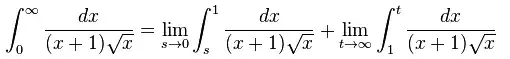
(both above are from Wikipedia.org)

Ben Kovitz
  • 27,566
  • 3
  • 53
  • 109
Listenever
  • 24,139
  • 38
  • 136
  • 254

6 Answers6

25

Here's how I'd say the first one:

The absolute value of S minus the sum from 1 to n of f of t sub i times delta sub i is less than epsilon.

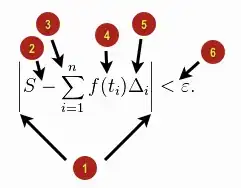
enter image description here

Key:

(1) The absolute value of
(2) S minus
(3) the sum from 1 to n of
(4) f of t sub i
(5) times delta sub i
(6) is less than epsilon

Note: Some mathematical expressions can be read aloud in more than one way. For example, someone might say:

  • sigma instead of the sum of
  • the function instead of f of
  • delta i instead of delta sub i
  • t sub i delta sub i instead of t sub i times delta sub i
Community
  • 1
J.R.
  • 109,547
  • 9
  • 164
  • 291
  • 4
    Note that, in a context where you know that the subscripts are there, you might just say "t i delta i". Indeed, even if the person you're talking to doesn't know there are subscripts, they'll probably guess that's what you mean, since you'd probably say "t delta i squared" if you meant "t times i times delta times i". – David Richerby Dec 14 '14 at 14:31
  • 1
    For summation, many people also read it as "the sum from i equals 1 to n of..." or "the sum as i goes from 1 to n of..." – user3932000 Apr 14 '16 at 04:17
  • For clarity I like having something along the lines of "all" to indicate closing of non-parenthesized expression - here it is quite obvious, but if 'less than' would be 'plus', and the whole thing would be an expression, it would be helpful – Sebi Aug 18 '16 at 10:07
  • I really like the legend. – DavidHyogo Sep 21 '18 at 12:26
16
  • The absolute value of the difference between S and
  • the sum from i equals one through i equals n of
  • the function f evaluated at t sub i times the width of each i
  • is less than epsilon.

If it is clear that i and n are one-indexed, then "the sum from i equals one through i equals n" can be replaced by "the sum of the first n terms". "The width of each i" is an interpretation of "delta i".

  • The function is one divided by the quantity x plus one close quantity, all divided by the square root of x.
  • The integral from zero to infinity of the function d x
  • equals the limit as s goes to zero of the integral from s to 1 of the function d x
  • plus the limit as t goes to infinity of the integral from 1 to t of the function d x.

"Goes to" can be replaced by "goes toward", or (as Damkeng suggests) "tends to", or (as J.R. suggests) "approaches".

I often use a notation like "integral from x equals a to x equals b" instead of "integral from a to b". I also often say "to positive infinity" instead of "to infinity".

I "factored out" the definition of the function in the first sentence. If the function were easy to say (such as "x squared"), I would not "factor out" the definition of the function. Instead, I would include the "x squared" in the statements of the integrals, a la Damkeng's answer.

Jasper
  • 24,268
  • 4
  • 54
  • 86
  • Don't you ever read 'integral' as 'sum'? – Listenever Dec 14 '14 at 06:54
  • 2
    I was taught to use the terms "integral" and "integration" for the various integral signs (such as "∫", "∬", "∭", "∮", "∯", and "∰"). Similarly, I was taught to use the d notation for full derivatives with respect to a variable, and the partial notation for partial derivatives with respect to a variable. – Jasper Dec 14 '14 at 07:56
  • 1
    I often say "double integral" when performing either an integral of an integral (such as ∬ a dx dy ) or an area integral (such as ∫ a dA ) or a surface integral (such as ∯ a dA ). Similarly, I often say "triple integral" or "volume integral" when performing either an integral of an integral of an integral (such as ∭ a dx dy dz ) or a volume integral (such as ∫ a dV ). – Jasper Dec 14 '14 at 07:59
  • 3
    I was taught to use the term "sum" for discrete sums, such as when the (capital) "sigma" notation ( "" ) is used. I use the term "series" to refer to the sequence generated by evaluating the sum for the various values of n. For example, "1, 2, 3, 4, …" is the sequence of integers. "1, 1/2, 1/4, 1/8, …" is a corresponding geometric sequence. "1, 3/2, 7/4, 15/8, …" is the corresponding series, where each item in the series is the sum of the first i elements of the geometric sequence. – Jasper Dec 14 '14 at 08:07
  • I think "approaches" can also be used in lieu of "goes to". – J.R. Dec 14 '14 at 11:17
  • offtopic: nice to know that you call it "limit". In germany we say "limes" (see: http://en.wikipedia.org/wiki/Limes). Until now I thought "lim" stands for "limes" and everyone in the world call it so :-D – Munchkin Dec 15 '14 at 12:56
  • @Munchkin Actually, "limit" is just līmes imported into English in the usual way, making the stem into a word on its own rather than using the nominative. – Ben Kovitz May 26 '15 at 18:35
  • This is really, really wordy, and very few people will actually read it like this. – user3932000 Apr 14 '16 at 04:18
  • If we stick to the official (modern) usage of the word "function", then saying "the function is one divided by x ..." is not correct, since 1/x is not a function. It would have been correct in pre 1930 mathematics. Some details on the history can be found here. – Michael Bächtold Sep 05 '19 at 06:48
  • I wouldn't trust an English dictionary to give a precise definition of a mathematical term. 1/(x+1)sqrt(x) is not a mapping, since it doesn't come with the information of what the input variable is. You might think it's obviously x, but what if we had previously declared that x=t^2. Then 1/(x+1)sqrt(x)=1/(t^2+1)|t|. The left and right hand side are equal, but are they the same mapping? What is the input variable of this object? – Michael Bächtold Sep 05 '19 at 11:01
  • Actually, Collins 5th is not the same as its 4th definition of function. The 5th is about "function of" which is not defined in modern mathematics and not the same as a mapping. This is precisely the distinction of the pre- and post 1930 definition of the word "function" in mathematics. See the link in my first comment. – Michael Bächtold Sep 05 '19 at 11:07
  • @MichaelBächtold -- Here is the technical definition I am using: "A function f from a set X to a set Y is a correspondence that assigns to each element x of X a unique element y of Y. The element y is called the image of x under f and is denoted by f(x). The set X is called the domain of the function. The range of the function consists of all images of elements of X." Swokowski's next sentence is, 'The symbol f(x) used for the element associated with x is read "f of x."' – Jasper Sep 05 '19 at 18:26
  • I fully agree with that definition. So when we write f(x) = 1/(x+1)sqrt x , then f is the function, and not f(x). Hence 1/(x+1)sqrt x cannot be the function since it is the same as f(x). But again: that is the modern definition. For 200 years it was correct to say f(x) is a function of x, or 1/(x+1)sqrt x is a function of x etc. – Michael Bächtold Sep 06 '19 at 06:41
  • @MichaelBächtold -- Either you are making a distinction that the English language does not make, or English-speakers are quite happy to use a complete description of the implementation of a function as a name for that function. – Jasper Sep 06 '19 at 16:23
  • Again: 1/(x+1)sqrt x is not a full description of a function. A full description would be x |--> 1/(x+1)sqrt x, using mathematical notation. Using python notation the same might be written as lambda x:1/((x+1)*sqrt(x)). Unfortunately, not only English-speakers are quite happy to do what you are suggesting. In German, Italian, French etc. people do the same. This has historical reasons, but mathematically it's wrong, if we stick to the modern definition of "function". – Michael Bächtold Sep 06 '19 at 20:36
10

Although not a direct answer to your question, here are a few references on how to read mathematical symbols and expressions. As a non-native English speaker who has to read mathematical formulae, I've found them pretty useful.

  1. Handbook for Spoken Mathematics, Research and Development Institute, Inc: This is probably the most complete reference. A more user friendly format of its content can be found in this pdf.
  2. H. Valiaho, Pronunciation of mathematical expressions (pdf): A short list divided by topic (e.g. Logic, Sets, Functions etc.). Reports also variants.
  3. K. Kromarek, Mathematics Pronunciation Guide: This is a guide on how to pronounce mathematical symbols and names, but not on how to read expressions.
Pieter Fleurinck
  • 3
  • 2
Massimo Ortolano
  • 417
  • 1
  • 5
  • 16
9

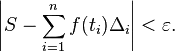
the first example

Absolute value of s minus sum i equals one to n, of f of t i times delta i, is less than epsilon.

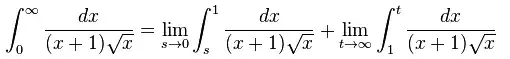
the second example

Integral from zero to infinity of dx by x plus one times square root of x is equal to the limit of integral from s to one of dx by x plus one times square root of x as s tends to zero plus the limit of integral from one to t of dx by x plus one times square root of x as t tends to infinity.

Please note that this is a casual reading. It's practically impossible to avoid ambiguity when reading mathematical expressions aloud. We might try to add more words such as "left parenthesis", "right parenthesis", and so on, but that wouldn't help much. There are several possible alternatives, but this is how I normally read them.

Damkerng T.
  • 27,174
  • 10
  • 70
  • 161
3

The simple answer is "you don't". Complex mathematical expressions like those become ambiguous when read out loud because you lose a lot of the structure. If you ever need to communicate the expression exactly, you'd write it down and point to it.

The only exception I can think of is if you were dictating something over the telephone, for example because you were working on a paper with somebody and you were trying to point out a mistake. Then, you'd read out literally every symbol. (Or just the part with the mistake, e.g., "The sum should be from i equals 0 to n minus 1, not 1 to n.")

David Richerby
  • 8,055
  • 27
  • 45
  • Commonly lecturers will read out loud as they write on the board, whether for the benefit of those with obstructed sightlines or just to fill the time. I've had professors who used the word "quantity" to introduce large sections within brackets, and "onto" for "times" but with the implication that it's outside a prior term. So this would be "absolute value of quantity ess minus sum from 1 to n of f of tee sub eye onto delta sub eye", pause and breath, "less than epsilon". – CCTO Jan 06 '21 at 03:06
1

As a mathematician, a physicist and a uni lecturer, I would read the two expressions above as follows:

(1) the absolute value of S minus the sum of "f at t sub i" times "delta sub i", where i changes from 1 to n, is less than epsilon.

(2) the x integral from zero to infinity of the function "1 over '(x plus 1) times (square root of x)' " is equal to the limit of x integral from s to 1 of the function as s tends to zero, plus the limit of x integral from 1 to t of the function as t tends to infinity.

At a class, you point to the relevant positions of the expressions while you read them. Note that clarity and simplicity in statements are important in teaching.

Wilford Lie
  • 11
  • 1