P-value hacking

Question

P-value hacking is the "art" of looking at different outcomes and specifications until you get a "false positive", i.e. a p value under, say, 0.05, which only noise and not true under the data generating process.

Say I have a treated group with size $N$ and a control group with size $M$, $K$ outcome variables, and am targeting a p-value of $p$: How can I compute the ex-ante probability of getting at least one false positive significant result significant under $p$?

You can assume that the $K$ characteristics are independently and normal distributed, and if it simplifies a lot, that $M=N$.

Answer 1

Under the assumption of i.i.d. Normal characteristics, the situation described is taken care by separate Welch's t-tests that account for possibly different sample sizes and different variances. Denote the statistics of these tests $t_j, j=1,...,K$. The p-value associated with each is

$$p_j = \Pr\big(|t_j|\geq t(\alpha)\mid H_0\big) $$

where $H_0$ is the hypothesis that the populations means between treated and controlled group are equal, and $t$ depends on the significance level $1-\alpha$.

We can write the probability in terms of the corresponding cumulative distribution function,

$$\Pr\big(|t_j|\geq t(\alpha)\mid H_0\big) = 1 - F(|t_j|)$$

Therefore

$$p_j = 1 - F(|t_j|) \implies 1-p_j = F(|t_j|)$$

If we contemplate the situation a priori, before even looking at the data, then the p-values lie in the future and can be modelled as random variables. Viewed as a random variable, the probability integral transform tells us that $1-p_j$ follows a $U(0,1)$ Uniform distribution, and by the properties of this distribution so does $p_j$.

Collecting all $p_j$, we have a sample of size $K$ of independent $U(0,1)$ uniforms. The probability that at least one of them is smaller than a specific value, say $p^*$, is equal to the probability that the minimum of them is lower than this threshold. This can be understood as follows:

$$\Pr\Big (\text {At least one $p_j \leq p^*$} \Big) = \Pr\Big (\text {Not all $p_j > p^*$} \Big) $$

$$ = 1-\Pr\Big (\text {All $p_j > p^*$} \Big) = 1- \prod_{j=1}^K \Pr\Big ( p_j > p^* \Big)$$

due to independence, and so, since they are identically distributed,

$$\Pr\Big (\text {At least one $p_j \leq p^*$} \Big) = 1- \left [1-\Pr\Big ( p \leq p^* \Big)\right]^K = 1 - \left [1-F_U \big(p^* \big)\right]^K$$

But this is the cumulative distribution function of the minimum of $K$ i.i.d random variables.

Denote this minimum $p_{(1)}$.

The CDF of the minimum of $K$ independent $U(0,1)$ variables is

$$F_{p_{(1)}}(p_{(1)}) = 1 - \big [1-p_{(1)}\big]^K$$

We want the probability

$$ \Pr(p_{(1)} \leq p^*) = 1- \big [1-p^*\big]^K$$

Indicative values:

Answer 2

I agree with @AlecosPapadopoulos we want something like: $$ \Pr(p_{(1)} \leq p^*) = 1- \big [1-p^*\big]^K$$ But I don't see how $n$ and $M$ couldn't enter into the proper test statistic. For example, if the underlying data is normally distributed i.i.d. data then $N$ and $M$ do matter.

Consider that noise mean $\mu$ and variance $\sigma$, which, by assumption is the same for the control and "treated" group. The mean of the treated group with size N will be distributed $N(\mu, \sigma^2 / n)$ and $N(\mu, \sigma^2 / M)$ for the control. So the difference in means will be distributed $$N(0, \sigma^2 / n + \sigma^2 / m)$$

But you won't know $\sigma$ or $\mu$, so we'll have to estimate it with $X_1$, $X_2$, and $s_{X_1X_2}$, and use a t-test. This setup gives a t-statistic like this: $$t = \frac{\bar {X}_1 - \bar{X}_2}{s_{X_1 X_2} \cdot \sqrt{\frac{1}{n}+\frac{1}{m}}}$$ where $$s_{X_1X_2} = \sqrt{\frac{(n-1)s_{X_1}^2+(m-1)s_{X_2}^2}{n+m}}.$$ SRC: Student's t-test on Wikipedia

The unpaired sample t-test for this difference in means has degrees of freedom $N-M-2$. Therefore the rejection region should depend on both n and m, both in what critical value of the test to use through the degrees of freedom of that test and the test statistic calculation itself.

Answer 3

The other answers are good, but I thought that another answer with a slighlty different focus might be a good complement.

Does the sample size usually affect the false-positive rate?

Judging from the comments, I think that the question has been prompted by this article, which includes a couple of mistakes (or at least miswordings).

Firstly (and most worryingly in general) it defines p-values incorrectly, but more relevantly it includes the sentence "If you measure a large number of things about a small number of people, you are almost guaranteed to get a “statistically significant” result."

The p-value is the probability, assuming that the null hypothesis is true, of observing a result as least as extreme as the one that was actually observed. As pointed out in the other answers, this means that it should be uniformly distributed between 0 and 1 regardless of sample size, underlying distributions, etc.

So the sentence should have read "If you measure a large number of things about a small number of people, you are almost guaranteed to get a “statistically significant” result."

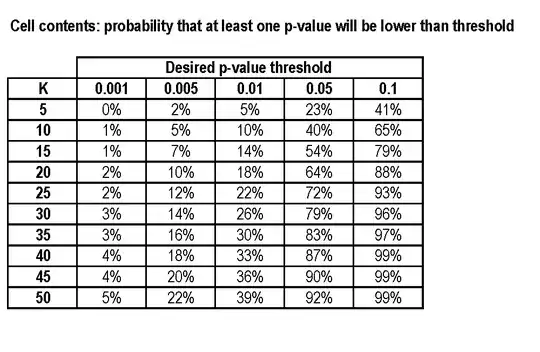
As correctly calculated in the article, even if chocolate does exactly nothing there was a 60% chance (assuming independence, etc.) of getting a significant result.

They actually got three significant results, which is quite surprising (p=0.06 under the -- probably unrealistic -- assumption of independence).

Does the sample size ever affect the false-positive rate?

Actually sometimes it does, though it only really makes a difference if the sample size is really small.

I said that (assuming that the null hypothesis is true) the p-value should be uniformly distributed. But the uniform distribution is continuous, while a lot of data is discrete with only finitely many possible outcomes.

If I toss a coin a few times to check whether it is biased, there are only a few possible outcomes and hence a few possible p-values, so the distribution of the potential p-values is a very bad approximation to the uniform distribution. If I flip it few enough times, it might be impossible to get a significant result.

Here is an example of a case where that actually happened.

So you would have something like "If you measure certain types of things about a sufficiently small number of people, you are never going to get a “statistically significant” result, no matter how many things you try."

Does this mean that you shouldn't worry about the sample size if a result is positive?

No. Some positive results are false positives and some are true positives. As discussed above, it's usually safe to assume that the false-positive rate is fixed (generally at 5%). But a smaller sample size always makes true positives less likely (having a smaller sample size means that the test has lower power). And if you have the same number of false positives but fewer true positives, a randomly chosen positive result is more likely to be false.

Answer 4

There is one thing perhaps worth adding to the excellent answers above, which is there is essentially a meta-numbers game going on as well. Lets say that 20 scientists all do the same set of experiments looking for something possibly weakly correlated like "does chocolate cause heart attacks", and will accept the p value < 0.05 significant which frankly they shouldn't. The cumulative probability is that one scientist will get a significant finding, which is the one experiment that will get published, since negative results rarely get accepted. There is then a 100% chance that that finding will get picked up by the Bild Zeitungs of this world and mis-reported.

Unfortunately, because we don't report the absence of findings, we're essentially engaged in a planet wide exercise in reporting all the experiments that get lucky - in the wrong sense of the word.

For subjects with a strong theoretical basis, good experimental design provides some protection against this - for subjects which are pre-dominantly having to work with observational data, and try to work out the theory - like economics - it's a major issue.

Added: For an extensive - and very well written - discussion on the entire issue, see the paper that started the recent debate:

An Investigation of the false discovery rate and the misinterpretation of p-values David Colquhoun